概念:
在统计学中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)
1)计算期望(E),利用概率模型参数的现有估计值,计算隐藏变量的期望;
2)最大化(M),利用E 步上求得的隐藏变量的期望,对参数模型进行最大似然估计。
3)M 步上找到的参数估计值被用于下一个 E 步计算中,这个过程不断交替进行。
总体来说,EM的算法流程如下:
1.初始化分布参数
2.重复直到收敛:
E步骤:估计未知参数的期望值,给出当前的参数估计。
M步骤:重新估计分布参数,以使得数据的似然性最大,给出未知变量的期望估计。
预备知识
- 1 极大似然估计
(1)举例说明:经典问题——学生身高问题
我们需要调查我们学校的男生和女生的身高分布。 假设你在校园里随便找了100个男生和100个女生。他们共200个人。将他们按照性别划分为两组,然后先统计抽样得到的100个男生的身高。假设他们的身高是服从正态分布的。但是这个分布的均值μ和方差σ2我们不知道,这两个参数就是我们要估计的。记作θ=[μ,σ]T。
问题:我们知道样本所服从的概率分布的模型和一些样本,需要求解该模型的参数。如图
我们已知的有两个:样本服从的分布模型、随机抽取的样本;我们未知的有一个:模型的参数。根据已知条件,通过极大似然估计,求出未知参数。总的来说:极大似然估计就是用来估计模型参数的统计学方法。 (2)如何估计 问题数学化:设样本集X=x1,x2,…,xN,其中N=100 ,p(xi|θ)为概率密度函数,表示抽到男生xi(的身高)的概率。由于100个样本之间独立同分布,所以我同时抽到这100个男生的概率就是他们各自概率的乘积,也就是样本集X中各个样本的联合概率,用下式表示:
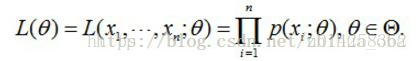
这个概率反映了,在概率密度函数的参数是θ时,得到X这组样本的概率。 我们需要找到一个参数θ,使得抽到X这组样本的概率最大,也就是说需要其对应的似然函数L(θ)最大。满足条件的θ叫做θ的最大似然估计量,记为
θ^=argmaxL(θ)
(3)求最大似然函数估计值的一般步骤 首先,写出似然函数:
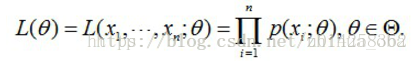
然后,对似然函数取对数:
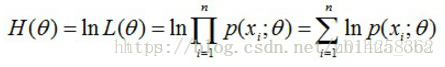
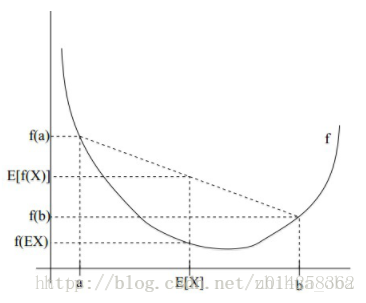
接着,对上式求导,令导数为0,得到似然方程; 最后,求解似然方程,得到的参数θ即为所求。 - **2 Jensen不等式** 设f是定义域为实数的函数,如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。 Jensen不等式表述如下:如果f是凸函数,X是随机变量,那么:E[f(X)]≥f(E[X])。当且仅当X是常量时,上式取等号。其中,E[x]表示x的数学期望。 例如,图2中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。X的期望值就是a和b的中值了,图中可以看到E[f(X)]≥f(E[X])成立。 注: 1、Jensen不等式应用于凹函数时,不等号方向反向。当且仅当X是常量时,Jensen不等式等号成立。 2、关于凸函数,百度百科中是这样解释的——“对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上非负,就称为凸函数(向下凸)”。关于函数的凹凸性,百度百科中是这样解释的——“中国数学界关于函数凹凸性定义和国外很多定义是反的。国内教材中的凹凸,是指曲线,而不是指函数,图像的凹凸与直观感受一致,却与函数的凹凸性相反。只要记住“函数的凹凸性与曲线的凹凸性相反”就不会把概念搞乱了”。关于凹凸性这里,确实解释不统一,博主暂时以函数的二阶导数大于零定义凸函数,此处不会过多影响EM算法的理解,只要能够确定何时E[f(X)]≥f(E[X])或者E[f(X)]≤f(E[X])就可以。
EM算法详解
- 1 问题描述
我们目前有100个男生和100个女生的身高,共200个数据,但是我们不知道这200个数据中哪个是男生的身高,哪个是女生的身高。假设男生、女生的身高分别服从正态分布,则每个样本是从哪个分布抽取的,我们目前是不知道的。这个时候,对于每一个样本,就有两个方面需要猜测或者估计: 这个身高数据是来自于男生还是来自于女生?男生、女生身高的正态分布的参数分别是多少?EM算法要解决的问题正是这两个问题。如图
- 2 EM算法推导
样本集X={x1,…,xm},包含m个独立的样本;每个样本xi对应的类别zi是未知的(即上文中每个样本属于哪个分布是未知的);我们需要估计概率模型p(x,z)的参数θ,即需要找到适合的θ和z让L(θ)最大。根据上文2.1 极大似然估计中的似然函数取对数所得logL(θ),可以得到如下式:
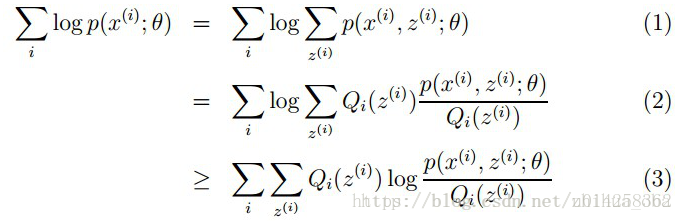
其中,(1)式是根据xi的边缘概率计算得来,(2)式是由(1)式分子分母同乘一个数得到,(3)式是由(2)式根据Jensen不等式得到。 这里简单介绍一下(2)式到(3)式的转换过程:由于∑Qi(z(i))[p(x(i),z(i);θ)Qi(z(i))]为p(x(i),z(i);θ)Qi(z(i))的期望,且log(x)为凹函数,根据Jensen不等式(当f是凸函数时,E[f(X)]≥f(E[X])成立;当f是凹函数时,E[f(X)]≤f(E[X])成立)可由(2)式得到(3)式。此处若想更加详细了解,可以参考博客the EM algorithm。 上述过程可以看作是对logL(θ)(即L(θ))求了下界。对于Qi(z(i))的选择,有多种可能,那么哪种更好呢?假设θ已经给定,那么logL(θ)的值就取决于Qi(z(i))和p(x(i),z(i))]了。我们可以通过调整这两个概率使下界不断上升,以逼近logL(θ)的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明我们调整后的概率能够等价于logL(θ)了。按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到: p(x(i),z(i);θ)Qi(z(i))=c c为常数,不依赖于z(i)。对此式做进一步推导:由于∑z(i)Qi(z(i))=1,则有∑z(i)p(x(i),z(i);θ)=c(多个等式分子分母相加不变,则认为每个样例的两个概率比值都是c),因此得到下式:
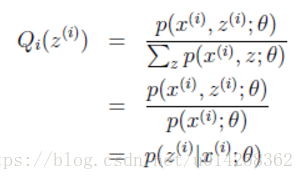
至此,我们推出了在固定其他参数θ后,Qi(z(i))的计算公式就是后验概率,解决了Qi(z(i))如何选择的问题。这一步就是E步,建立logL(θ)的下界。接下来的M步,就是在给定Qi(z(i))后,调整θ,去极大化logL(θ)的下界(在固定Qi(z(i))后,下界还可以调整的更大)。这里读者可以参考文章EM算法。 3.3 EM算法流程 初始化分布参数θ; 重复E、M步骤直到收敛: E步骤:根据参数θ初始值或上一次迭代所得参数值来计算出隐性变量的后验概率(即隐性变量的期望),作为隐性变量的现估计值:
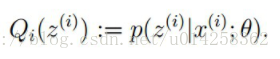
M步骤:将似然函数最大化以获得新的参数值:
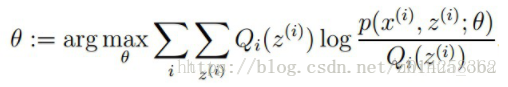
EM算法优缺点以及应用
优点:稳定上升的步骤能非常可靠地找到“最优的收敛值”。 有时候缺失数据并非是真的缺少了,而是为了简化问题而采取的策略,这时EM算法被称为数据添加技术,所添加的数据通常被称为“潜在数据”,复杂的问题通过引入恰当的潜在数据,能够有效地解决我们的问题。
缺点:对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
EM算法的应用:k-means算法是EM算法思想的体现,E步骤为聚类过程,M步骤为更新类簇中心。GMM(高斯混合模型)也是EM算法的一个应用,感兴趣的小伙伴可以查阅相关资料。
文章参考
https://blog.csdn.net/zhihua_oba/article/details/73776553

