解释一:
假设费用函数 L 与某个参数 x 的关系如图所示:
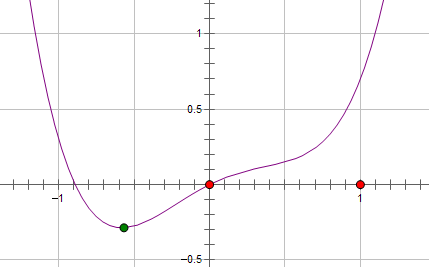
则最优的 x 在绿点处,x 非零。
现在施加 L2 regularization,新的费用函数()如图中蓝线所示:

最优的 x 在黄点处,x 的绝对值减小了,但依然非零。
而如果施加 L1 regularization,则新的费用函数()如图中粉线所示:
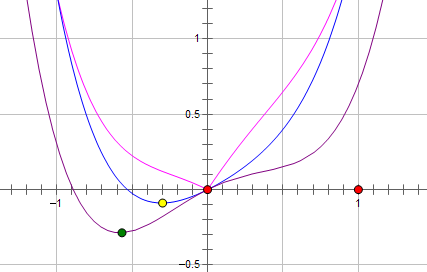
最优的 x 就变成了 0。这里利用的就是绝对值函数的尖峰。
两种 regularization 能不能把最优的 x 变成 0,取决于原先的费用函数在 0 点处的导数。
如果本来导数不为 0,那么施加 L2 regularization 后导数依然不为 0,最优的 x 也不会变成 0。
而施加 L1 regularization 时,只要 regularization 项的系数 C 大于原先费用函数在 0 点处的导数的绝对值,x = 0 就会变成一个极小值点。
上面只分析了一个参数 x。事实上 L1 regularization 会使得许多参数的最优值变成 0,这样模型就稀疏了。
解释二:
很多人贴PRML书里的那个图,但是感觉很多人有疑问,原本我要优化的是包含正则项的损失,这两个应该是一起优化的,为什么在图里把它们拆解了,其实PRML书里也说得很明白,我再说得具体点。
首先,我们要优化的是这个问题 。
其次, 和
这个优化问题是等价的,即对一个特定的 总存在一个
使得这两个问题是等价的(这个是优化里的知识)。
最后,下面这个图表达的其实
这个优化问题,把 的解限制在黄色区域内,同时使得经验损失尽可能小。

解答三:直观上来理解一下, 对损失函数施加 L0/L1/L2 范式约束都会使很多参数接近于0. 但是在接近于0的时候约束力度会有差别. 从导数的角度看, L1正则项 在0附近的导数始终为正负1, 参数更新速度不变. L2 在0附近导数接近于0, 参数更新缓慢. 所以 L1 相比 L2 更容易使参数变成0, 也就更稀疏
个人最喜欢第二种解释