目录
回顾复数
复数的基本运算
回顾复数
将下列数字写成复数形式:
-21
7i
简单复习一下,复数是包含实数部分和虚数部分的数。
如果有a+bi,a是实数,b是实数,这是复数。a是实部,bi是虚数部分(注:虚部不包括i)。
为什么bi是虚部?因为bi带有特殊系数i,这个虚数单位,这个特殊的数i,在这里乘以了b。我相信大家都会觉得怪诞,不过根据定义:
在此之前,不存在对某个数取平方后得到-1,现在取i的平方,得到-1,关于虚数(单位)的特别的知识点是它的平方是负数。复数有用之处在于它使我们有能力解决很多方程,这些方程在只允许实数解的情况下无解。复数在很多方面都有用,特别是在工程领域,还有其他领域,比如物理等等。现在,我们不会花很多心思讨论复数定义,在大家处理更多数字后,特别是接触到某些工程应用后,希望大家明白虚数的价值。
回到问题中来,把上面的数字写成复数形式。
-21
怎么把它写成复数呢?把它写成实部和虚部的组合。可以写成:
-21 = -21+0i
0i等于0,所以它仍等于-21,实际上这里没有虚部,-21本身就是复数形式,很简单。同样的:
7i = 0 + 7i
7i是虚数形式的,所以这里没有实部,实部是0,虚部是7i,所以等于0 + 7i。
复数的基本运算
很多时候解方程都会碰到根号下负数的情况,比如根号下-1或者-9:
由于如何实数的平方不是0就是正数,所以以上两个数这些没有定义,为了定义这些数,人们引入i的概念,i是虚数单位,i的定义是:
这就是解决了根号下负数的问题,这样一来,根号下-9是多少呢?它等于i乘以根号9,即3i,
为什么,想想3i平方是多少?
这是指数性质。所以,这样的定义就拓展到了,所有负数开根号的情况:
3i是所谓的虚数,它其实也不比其他数“虚”,某种意义上,负数真的存在吗?只不过是将负号放在前面表示抽象含义,负号只是表示它和大小的关系。任何数乘以虚数单位i都是虚数。解二次方程时,你会发现结果有时会实数和虚数并存(有实数部分和虚数部分),举个例子:
5 + 2i
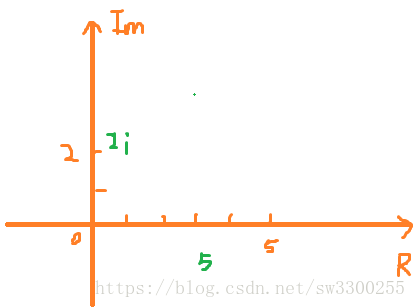
这不能化简了,因为实数和虚数不能相加,大家可以把这当作不同维度,一个数有实部5,还有虚部2i,这叫做复数。复数可以在平面中表示:
虚数也就是虚轴,在纵轴2i,上图表示为2个单位。
实数也就是实轴,在实轴5,上图表示为5个单位。
所以这个图形表示为:5+2i。在以后讲复数应用时,我还会举更多例子,现在只需要知道定义即可。看看有什么运算,两复数相加怎么做:
a是实部,bi是虚部,另一个复数是:
通常像方程的未知数,这样的一般性实数,人们喜欢用x,而复数的惯例是用z表示。比如:
表示任意某个复数,那么
等于多少呢?
复数相加只需要分别把实部和虚部相加即可,这等于:
那么两个复数相减呢?如下:
这就是新的复数。
那么两个复数相乘呢?如下:
教科书的方法称为FOIL,大概是八九年级的方法,我不怎么喜欢它,我喜欢将这看成是两次使用分配率,这里,可以将(c+di)分配到(a+bi)中的a和bi这2项中。我们得到:
分解得:
化简得:
实数很简单,下一次我们会谈到实数。这里的关键是使用分配率,然后实部相加,实数和虚数不可相加,然后虚部相加,记住,两个虚数相乘时,i和i相乘会得到-1。
那么两个复数相除呢?
我们要用到一个性质,但愿大家学过:
如果这两个复数相乘:
那么是多少?
。我们最后得到
,非常有趣,这是一个复数乘以另外一个复数,两个复数很像,只是虚部方向相反。两者相乘得到一个实数,i都消去了。
例子用的是,即
,那么
称为
的共轭复数。这个术语需要了解,共轭的符号是顶上一横,
的共轭是
,反过来
的共轭是
,如下:
两者互为共轭。的共轭是
,共轭其实只是改变虚轴上的方向。好了,回到之前的题目。共轭只是做除法时需要的工具。复数乘以其共轭等于实数,我们还知道,任意数乘以1还是该数,那么,分子分母同时乘以分母的共轭复数,看看得到什么:
我们将得到什么?
这是结果,代数运算的话,只能实部和实部相加,虚部和虚部相加,化简,先看实部:
这看起来也许不像复数,将实部和虚部分开就像了。
注意加减时,实部和虚部间不可以合并,顶多只能数乘虚数,这就是我们所做的。这里乘,写成字母形式,除法有点复杂。下面举个例子,实际数例就不会显得那么复杂了:
乘以分母的共轭复数:
这是1,不会改变值,分母很容易求出:
然后写成一般形式:
复数除以复数,结果仍是复数。你们可以练习一下,随便找一下复数,在复平面画一下,看加减乘除时是什么情况,看数乘和取共轭时又是什么情况,这能让大家更好地理解复数。
——请不断重复练习、练习、练习、再练习。。。