Java 数据结构和算法 - 递归

什么是递归

recursive method就是直接或者间接地调用自己的方法。许多算法都适合用递归形式表达。

背景：数学归纳法证明

下面的定理，使用其他方法也可以证明，但是，数学归纳法是最简单的：
对于任何大于等于1的正整数，前N个数的和
$\sum_{i=1}^{N}i = 1+2+...+N，等于N(N+1)/2$

下面是证明过程：
很明显，如果N=1,定理是正确的。假设对于1≤N≤k是真的。那么
$\sum_{i=1}^{k+1}i = k+1 + \sum_{i=1}^{k}i$
根据假设，定理对于k是真的，所以
$\sum_{i=1}^{k+1}i = k+1 + k(k + 1) / 2$
化简
$\sum_{i=1}^{k+1}i = (k + 1)(k + 2) / 2$

基本递归

有时候，数学函数是使用递归定义的。比如，让S(N)是前N个整数的和。那么S(1) = 1，我们可以写S(N) = S(N – 1) + N。在这里，我们根据函数S的自身的小实例定义自己。

        public static long s(int n) {
            if (n == 1)
                return 1;
            else
                return s(n - 1) + n;
        }

递归的基本规则

• Base case：不用递归的实例
• Make progress：任何递归都向着Base case发展

printing numbers in any base

比如我们要打印一个10进制正整数，每次打印一位。比如要打印1369，先是1，然后是3,然后是6,最后是9。
要决定最后一位很容易，因为n%10（n小于10的时候）就是。但是，前面几位怎么办？使用递归可以很容易地解决。

        public static void printDecimal(long n) {
            if (n >= 10)
                printDecimal(n / 10);
            System.out.print((char) ('0' + (n % 10)));
        }

其他进制的数字也很容易打印

        private static final String DIGIT_TABLE = "0123456789abcdef";
    
        public static void printInt(long n, int base) {
            if (n >= base)
                printInt(n / base, base);
            System.out.print(DIGIT_TABLE.charAt((int) (n % base)));
        }

完整版本是

public class PrintInt {
    private static final String DIGIT_TABLE = "0123456789abcdef";
    private static final int MAX_BASE = DIGIT_TABLE.length();

    private static void printIntRec(long n, int base) {
        if (n >= base)
            printIntRec(n / base, base);
        System.out.print(DIGIT_TABLE.charAt((int) (n % base)));
    }

    public static void printInt(long n, int base) {
        if (base <= 1 || base > MAX_BASE)
            System.err.println("Cannot print in base " + base);
        else {
            if (n < 0) {
                n = -n;
                System.out.print("-");
            }
            printIntRec(n, base);
        }
    }

    public static void main(String[] args) {
        for (int i = 0; i <= 17; i++) {
            printInt(1000, i);
            System.out.println();
        }
        printInt(0x5DEECE66DL, 10);
        System.out.println();
    }
}

它为什么有效

当设计一个递归算法的时候，我们总是假设递归调用会工作。
和其他方法一样，递归方法也是要和其他方法组合起来解决问题，不过，所谓的其他方法可能就是该递归方法以前的实例。

如何工作

Java和C++一样，也是通过使用内部堆栈的激活记录（activation record）来实现方法。激活记录包含方法的相应信息，比如参数的值和局部变量。激活记录的实际信息是和系统相关的。
使用激活记录栈，是因为方法以它们的调用顺序相反的顺序返回。一般来说，栈顶保存的是当前执行的方法。当方法G被调用，它的激活记录就被push到栈，这样G成了当前的活动方法。当方法返回，栈pop，当前的活动方法成了栈顶上的新值。

递归太多是危险的

比如斐波那契数F0, F1, … , Fi是这样定义的：F₀=0, F₁=1，第i个斐波那契数等于第i-1个数和第i-2个数的和，即F_i = F_i-1 + F_i-2。

    public static long fib( int n ) {
        if(n <= 1)
            return n;
        else
            return fib(n - 1) + fib(n - 2);
    }

上面这个算法就设计得不好。在我们相对比较快的机器上，计算F₄₀需要花费大约一分钟的时间，看下图，显示了计算的轨迹。

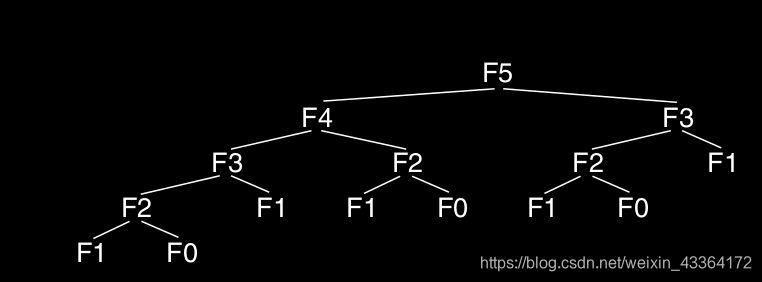
可以看到，做了大量的重复计算。要计算ib(n)，我们递归计算fib(n-1)。当这个递归调用返回以后，我们使用另一个递归调用计算fib(n-2)。但是，在计算fib(n-1)的时候，我们已经计算过fib(n-2)了，所以，再计算一次fib(n-2)就属于浪费了，是重复计算。
每调用fib(n-1)和每次调用fib(n-2)都要调用fib(n-3)，这样fib(n-3)被计算了三次。更悲惨的是，每次调用fib(n-2)或者调用fib(n-3)都要调用fib(n-4)，这样fib(n-4)被调用了五次。这样，我们的计算有大量的重复。
让C(N)是计算fib(n)的过程中，调用fib的次数。很明显C(0) = C(1) = 1。对于N ≥ 3，C(N) = F_N+2 + F_N-1 - 1。于是，对于N = 40, F₄₀ = 102,334,155，总的调用次数超过3亿次。

所以，递归调用的时候，不要做重复的工作。

树

操作系统保存文件一般都使用数结构或者类似树的结构。树也用来实现编译器、文本处理和搜索算法。

看一个二分搜索的例子：

        public static <AnyType extends Comparable<? super AnyType>>
        int binarySearch(AnyType[] a, AnyType x) {
            return binarySearch(a, x, 0, a.length - 1);
        }
    
        /**
         * Hidden recursive routine.
         */
        private static <AnyType extends Comparable<? super AnyType>> int binarySearch(AnyType[] a, AnyType x, int low, int high) {
            if (low > high)
                return NOT_FOUND;
            int mid = (low + high) / 2;
            if (a[mid].compareTo(x) < 0)
                return binarySearch(a, x, mid + 1, high);
            else if (a[mid].compareTo(x) > 0)
                return binarySearch(a, x, low, mid - 1);
            else
                return mid;
        }

再看一个分形的例子：

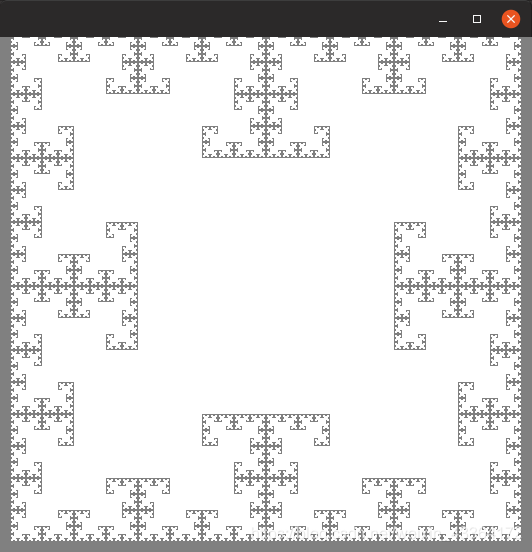
画布初始是灰色的，在画布上画白色的方格。最后一个方格画在中心位置。

import java.awt.Frame;
import java.awt.Graphics;
import java.awt.Color;

public class FractalStar extends Frame {
    private static final int theSize = 512;

    public void paint(Graphics g) {
        setBackground(Color.gray);
        g.setColor(Color.white);
        drawSpace(g, theSize / 2 + 10, theSize / 2 + 30, theSize);
    }

    private void drawSpace(Graphics g, int xCenter, int yCenter, int boundingDim) {
        int side = boundingDim / 2;

        if (side < 1)
            return;

        int left = xCenter - side / 2;
        int top = yCenter - side / 2;
        int right = xCenter + side / 2;
        int bottom = yCenter + side / 2;

        drawSpace(g, left, top, boundingDim / 2);
        drawSpace(g, left, bottom, boundingDim / 2);
        drawSpace(g, right, top, boundingDim / 2);
        drawSpace(g, right, bottom, boundingDim / 2);

        g.fillRect(left, top, right - left, bottom - top);
    }

    // Simple test program
    // For simplicity, must terminate from console
    public static void main(String[] args) {
        Frame f = new FractalStar();
        f.setSize(theSize + 20, theSize + 40);
        f.setVisible(true);
    }
}

数值应用

模幂运算

可用来实现hash表结构。
如果两个数A和B除以N的余数相同，我们就说他们同余N，写做A ≡ B (mod N)。于是

• 如果A ≡ B (mod N)，对于任何C，有A + C ≡ B + C(mod N)
• 如果A ≡ B (mod N)，对于任何D，有AD ≡ BD(mod N)
• 如果A ≡ B (mod N)，对于任何正的P，A^P ≡ B^P (mod N)
  比如，对于3333⁵⁵⁵⁵(mod 10)，因为3333 ≡ 3(mod 10)，所以我们需要计算3⁵⁵⁵⁵(mod 10)。因为3⁴=81，所以，3⁴ ≡ 1(mod 10)，再1388次幂得到3⁵⁵⁵² ≡ 1(mod 10)。两边都乘以3³ = 27,得到3⁵⁵⁵⁵ ≡ 27 ≡ 7(mod 10)，完成了计算。

接下来，我们看怎么高效计算X^N(mod P)。比较快的算法是，如果N是偶数，那么
X^N = (X ⋅ X)^N/2
如果N是奇数，那么
X^N = X ⋅ X^N-1 = X ⋅(X ⋅ X)^(N-1)/2

代码如下，我们在每个乘法之后有一个%运算。

    /**
     * Return x^n (mod p)
     * Assumes x, n >= 0, p > 0, x < p, 0^0 = 1
     * Overflow may occur if p > 31 bits.
     */
    public static long power(long x, long n, long p) {
        if (n == 0)
            return 1;
        long tmp = power((x * x) % p, n / 2, p);
        if (n % 2 != 0)
            tmp = (tmp * x) % p;
        return tmp;
    }

最大公约数

给两个正整数A和B，求他们的最大公约数gcd(A, B)，这个最大的整数D都可以被A和B整除。比如，gcd(70, 25) = 5。
我们可以很容易证明gcd(A, B) ≡ gcd(A – B, B)。因为D能被A和B整除，肯定也能被A – B和B整除。这样一直减下去，如果A小于B了，就用B-A，直到B为0,即gcd(A, 0) ≡ A，A就是答案。这个算法叫欧几里德算法，2000年前发明的。
更高效的算法是gcd(A, B) ≡ gcd(B, A mod B)，这是一个递归算法。于是，gcd(70, 25) ⇒ gcd(25, 20) ⇒ gcd(20, 5) ⇒ gcd(5, 0) ⇒ 5。

    /**
     * Return the greatest common divisor.
     */
    public static long gcd(long a, long b) {
        if (b == 0)
            return a;
        else
            return gcd(b, a % b);
    }

gcd算法用来解决类似的数学问题。对于方程AX ≡ 1(mod N)，A关于模N的乘法逆为X（1 ≤ X < N且1 ≤ A < N）。比如，3关于模13的乘法逆是9，即3⋅9 mod 13产生1。
计算乘法逆的能力是重要的，因为可以用来解诸如3i ≡ 7(mod 13)这样的方程。这些方程有很多应用，包括接下来要讨论的加密算法。在本例中，如果我们乘以3的逆（9），就得到i ≡ 63(mod 13)，所以i = 11。如果
AX ≡ 1(mod N),
那么 AX + NY = 1(mod N)，对于任何Y也是真的。对于某些Y，左边等于1。这样方程
AX + NY = 1
当A有乘法逆的时候，有解。
给定A和B，我们看怎样找到X和Y满足AX + BY = 1。我们假设0 ≤ ⎥B⎪ < ⎥A⎪，扩展gcd算法计算X和Y。首先，考虑基本情况，B ≡ 0，这样，我们不得不解AX = 1，这意味着A和X都是1。事实上，如果A不是1，就没有乘法逆。于是，只有当gcd(A, N) = 1时，A有模N的乘法逆。
然后考虑B不是0的情况。根据gcd(A, B) ≡ gcd(B, A mod B)，我们让A = BQ + R（Q是商、R是余数），这样递归地调用gcd(B, R)。假设我们能递归地解BX₁ + RY₁ = 1，因为R = A – BQ，我们有BX₁ + (A – BQ)Y₁ = 1，即AY₁ + B (X₁ – QY₁) = 1。这样，X = Y₁ 和 Y = X₁ – (A/B)Y₁是AX + BY = 1的解。

    // Internal variables for fullGcd
    private static long x;
    private static long y;

    /**
     * Works back through Euclid’s algorithm to find
     * x and y such that if gcd(a,b) = 1,
     * ax + by = 1.
     */
    private static void fullGcd(long a, long b) {
        long x1, y1;
        if (b == 0) {
            x = 1;
            y = 0;
        } else {
            fullGcd(b, a % b);
            x1 = x;
            y1 = y;
            x = y1;
            y = x1 - (a / b) * y1;
        }
    }

    /**
     * Solve ax == 1 (mod n), assuming gcd( a, n ) = 1.
     *
     * @return x.
     */
    public static long inverse(long a, long n) {
        fullGcd(a, n);
        return x > 0 ? x : x + n;
    }

rsa

首先，消息由由字符序列组成，每个字符都是位的序列。这样，消息也是位的序列，进而解释成一系列很大的数字。所以，我们要加密很大的数字，还要对加密后的结果解密。
RSA算法从接收者决定一些常量开始。首先，随机选择两个大的素数p和q。一般至少100位长。为了方便解释，我们假设p = 127，q = 211。接下来，接收者计算N = pq和N′ = (p – 1)(q – 1)，即N = 26,797， N′ = 26,460。接收者继续选择任何e > 1，使得gcd(e, N′) = 1（即e和N′互质）。假如选择了e = 13,379，接下来，d关于模N的乘法逆是e，计算结果是d = 11,099。
接收者计算出所有的常量，接下来：首先，销毁p、q和N′（只要任何一个被泄漏，安全性就受影响）。然后告诉任何想要给他发消息的人，使用e和N加密信息，接收者还保留d。要加密整数M，发送者计算M^e(mod N)，然后发送。假如M = 10,237，发送的值就是8422。当接收到加密的整数R，接收者就计算R^d(mod N)。对于R = 8,422，他得到原始值M = 10,237。
算法能工作，是因为选择的e、d和N满足M^ed = M(mod N)。N和e唯一地确定了d。这就叫公钥加密，任何想接收消息的人，都可以发布加密信息。
更快的办法是DES，很像RSA，DES是单key算法-使用相同的key加密和解密，很像门上的钥匙。问题是，单key算法需要双方共享key。怎么让一方确认另一方拥有key呢？可以使用RSA解决这个问题。一般是这样做的：
比如，Alice随机生成DES加密的key，然后使用DES加密消息。它把加密消息传给Bob。Bob要解密消息，就需要Alice使用的DES key。DES key比较短，所以Alice可以使用RSA加密DES key，然后送给Bob。Bob解密该消息，就有了DES key。

分治算法

divide-and-conquer 算法是一种有效的递归算法，由两部分组成：

• Divide：分成递归解决的小问题
• Conquer：根据子问题的解决，解决原始问题

最大连续子序列和问题

给定的整数（包括负数）A₁、A₂、…、A_N，找到 $\sum_{k=i}^{j}A_k$的最大值。如果所有的整数都是负数，最大连续子序列和是1。
有几个不同复杂度的算法。一个是穷举搜索的算法，效率最差（时间复杂度是O(N³)），选择每个子序列，求最大和。

    static private int seqStart = 0;
    static private int seqEnd = -1;
    
    /**
     * Cubic maximum contiguous subsequence sum algorithm.
     * seqStart and seqEnd represent the actual best sequence.
     */
    public static int maxSubSum1(int[] a) {
        int maxSum = 0;

        for (int i = 0; i < a.length; i++)
            for (int j = i; j < a.length; j++) {
                int thisSum = 0;

                for (int k = i; k <= j; k++)
                    thisSum += a[k];

                if (thisSum > maxSum) {
                    maxSum = thisSum;
                    seqStart = i;
                    seqEnd = j;
                }
            }

        return maxSum;
    }

基于每个新的子序列可以由先前的子序列在常量时间内计算出来的事实。因为我们有O(N²)个子序列，所以可以直接检查所有的子序列

    /**
     * Quadratic maximum contiguous subsequence sum algorithm.
     * seqStart and seqEnd represent the actual best sequence.
     */
    public static int maxSubSum2(int[] a) {
        int maxSum = 0;

        for (int i = 0; i < a.length; i++) {
            int thisSum = 0;
            for (int j = i; j < a.length; j++) {
                thisSum += a[j];

                if (thisSum > maxSum) {
                    maxSum = thisSum;
                    seqStart = i;
                    seqEnd = j;
                }
            }
        }

        return maxSum;
    }

也可以使用线性时间计算出来，只测试几个子序列

    /**
     * Linear-time maximum contiguous subsequence sum algorithm.
     * seqStart and seqEnd represent the actual best sequence.
     */
    public static int maxSubSum3(int[] a) {
        int maxSum = 0;
        int thisSum = 0;

        for (int i = 0, j = 0; j < a.length; j++) {
            thisSum += a[j];

            if (thisSum > maxSum) {
                maxSum = thisSum;
                seqStart = i;
                seqEnd = j;
            } else if (thisSum < 0) {
                i = j + 1;
                thisSum = 0;
            }
        }

        return maxSum;
    }

让我们考虑分治算法。假设输入是{4, –3, 5, –2, –1, 2, 6, –2}。我们把它从中间分成两半，最大和可能出现在

• 位于前一半
• 位于后一半
• 跨两个部分

我们先看第三种情况。要想避免独立考虑所有N/2个起点和N/2个终点的嵌套循环，可以使用两个连续循环代替两个嵌套循环。
这些连续循环，每个长度是N/2，组合起来只需要线性的时间。

看上图，对于前一半，计算每个数到最右边的子序列和。对于后一半，我们计算每一个到最左边的自序列和。我们可以组合这两个子序列形成跨两个部分的最大的连续子序列。和是两个子序列的和，即4 + 7 = 11。
算法的步骤是

• 递归计算位于前一半的最大连续子序列和
• 递归计算位于后一半的最大连续子序列和
• 通过两个连续循环计算，最大连续子序列和开始于前一半，结束于后一半
• 选择这三个和中最大的

    /**
     * Recursive maximum contiguous subsequence sum algorithm.
     * Finds maximum sum in subarray spanning a[left..right].
     * Does not attempt to maintain actual best sequence.
     */
    private static int maxSumRec(int[] a, int left, int right) {
        int maxLeftBorderSum = 0, maxRightBorderSum = 0;
        int leftBorderSum = 0, rightBorderSum = 0;
        int center = (left + right) / 2;

        if (left == right)  // Base case
            return a[left] > 0 ? a[left] : 0;

        int maxLeftSum = maxSumRec(a, left, center);
        int maxRightSum = maxSumRec(a, center + 1, right);

        for (int i = center; i >= left; i--) {
            leftBorderSum += a[i];
            if (leftBorderSum > maxLeftBorderSum)
                maxLeftBorderSum = leftBorderSum;
        }

        for (int i = center + 1; i <= right; i++) {
            rightBorderSum += a[i];
            if (rightBorderSum > maxRightBorderSum)
                maxRightBorderSum = rightBorderSum;
        }

        return max3(maxLeftSum, maxRightSum,
                maxLeftBorderSum + maxRightBorderSum);
    }

    /**
     * Return maximum of three integers.
     */
    private static int max3(int a, int b, int c) {
        return a > b ? a > c ? a : c : b > c ? b : c;
    }

    /**
     * Driver for divide-and-conquer maximum contiguous
     * subsequence sum algorithm.
     */
    public static int maxSubSum4(int[] a) {
        return a.length > 0 ? maxSumRec(a, 0, a.length - 1) : 0;
    }

动态编程

像前面的斐波那契数列的问题，要想使用好递归，可以使用动态编程重写递归算法-使用非递归的办法系统地在表格中记录子问题的解决。比如下面的找零钱问题
对于硬币C₁、C₂、…、C_N，找K美分至少需要多少枚硬币？
美分有一下几种面值：1、5、10和25（忽略不常用的50）。63美分可以由两个25美分、一个10美分和三个1美分组成，一共6枚硬币。对于美元来说，找零钱问题相对容易-我们重复使用可用的最大的硬币。我们可以证明，对于美国货币，这种方法总是最小化硬币的总数，这是贪心（greedy）算法的一个例子。
贪心算法中，每个阶段，作出的决定似乎是最佳的，不用考虑未来。当一个问题可以用贪心算法实现，我们确实很高兴-贪心算法通常符合我们的直觉，实现代码也不那么痛苦。不幸的是，有时候不能用贪心算法。如果美国有21美分面值的硬币，使用贪心算法，答案仍然是六枚，但是，最优解是三枚（都是21美分的）。
那么如何解决任意硬币组的问题呢？我们假设肯定有1分的硬币。一个简单的策略是使用下面的递归：

• 如果能恰好找一枚硬币，就是最小解
• 否则，对每个可能的值i，我们能分别计算i分和k-i分的最小值。然后选择最小的和所用的i

比如，让我们找63分。显然，一枚硬币是不行的。我们可以计算需要1分和62分（需要4枚）。我们递归地获得这些结果，认为他们是最佳的。如果我们分成2分和61分，递归解决产生2和4,一共6枚。我们继续尝试更多的可能，其中一部分见下图。终于，我们分成21和42分，之需要三枚硬币。最后，分成31和32分，一共需要5枚。最小值是3。

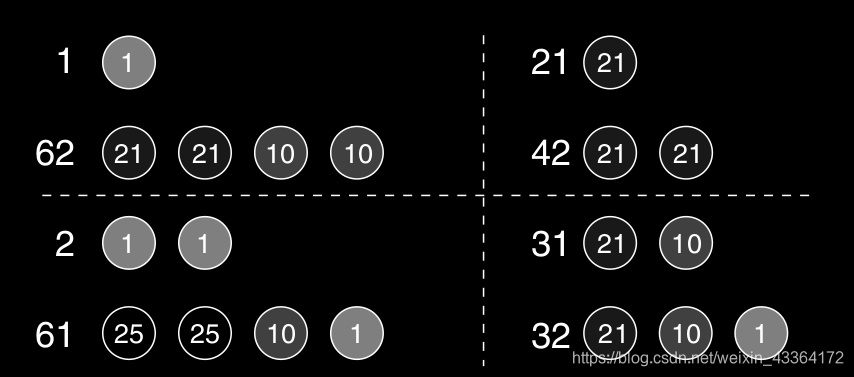
实现代码是

    // Return minimum number of coins to make change.
    // Simple recursive algorithm that is very inefficient.
    public static int makeChange(int[] coins, int change) {
        int minCoins = change;
        for (int i = 0; i < coins.length; i++)
            if (coins[i] == change)
                return 1;
        
            // No match; solve recursively.
        for (int j = 1; j <= change / 2; j++) {
            int thisCoins = makeChange(coins, j)
                    + makeChange(coins, change - j);
            if (thisCoins < minCoins)
                minCoins = thisCoins;
        }
        return minCoins;
    }

结果是正确的，但是，有很多重复计算，太浪费时间了。
替代算法是指定一个硬币来递归地减少问题。比如，对于63分，可以通过下面的方法：

• 一个1分加上递归的62分
• 一个5分加上递归的58分
• 一个10分加上递归的53分
• 一个21分加上递归的42分
• 一个25分加上递归的38分

见下图，只有五种递归调用。

代码如下

public class MakeChange {
    // Dynamic programming algorithm to solve change making problem.
    // As a result, the coinsUsed array is filled with the
    // minimum number of coins needed for change from 0 -> maxChange
    // and lastCoin contains one of the coins needed to make the change.
    public static void makeChange(int[] coins, int differentCoins,
                                  int maxChange, int[] coinsUsed, int[] lastCoin) {
        coinsUsed[0] = 0;
        lastCoin[0] = 1;

        for (int cents = 1; cents <= maxChange; cents++) {
            int minCoins = cents;
            int newCoin = 1;

            for (int j = 0; j < differentCoins; j++) {
                if (coins[j] > cents)   // Cannot use coin j
                    continue;
                if (coinsUsed[cents - coins[j]] + 1 < minCoins) {
                    minCoins = coinsUsed[cents - coins[j]] + 1;
                    newCoin = coins[j];
                }
            }

            coinsUsed[cents] = minCoins;
            lastCoin[cents] = newCoin;
        }
    }

    // Simple test program
    public static void main(String[] args) {
        // The coins and the total amount of change
        int numCoins = 5;
        int[] coins = {1, 5, 10, 21, 25};
        int change = 0;

        if (args.length == 0) {
            System.out.println("Supply a monetary amount on the command line");
            System.exit(0);
        }

        try {
            change = Integer.parseInt(args[0]);
        } catch (NumberFormatException e) {
            System.out.println(e);
            System.exit(0);
        }

        int[] used = new int[change + 1];
        int[] last = new int[change + 1];

        makeChange(coins, numCoins, change, used, last);

        System.out.println("Best is " + used[change] + " coins");

        for (int i = change; i > 0; ) {
            System.out.print(last[i] + " ");
            i -= last[i];
        }
        System.out.println();
    }
}