目录
@(树状数组算法详解·目录)
树状数组的引入
相信读者一定知道什么是前缀和,形如一串数\(a1,a2...,an,sum[i]=a[1]+a[2]+...+a[i]\)
前缀和在算法的优化上占有很重要的地位,一般就会预先对数据进行预处理运算以后,再在运算过程中用\(O(1)\)时间调用,这样的操作很大程度上避免了实际运算中的枚举,NOIP2016魔法阵就是一个典型的例题。
But前缀和也有其缺陷:
当原序列中的数据修改后如果快速调用前缀和??
在此,我们引入了一个名叫树状数组的算法,快速将单点修改和区间查询优化到\(O(logn)\)级别。
lowbit的含义
\(lowbit(i)\)表示非负整数i再二进制下最低位1以及末尾0的个数。
例如,二进制\(1001001100\)中,\(100\)的长度为\(3\),所以这个数字\(lowbit\)运算的结果为\(3\)。
根据计算机(dev-c++)的运算法则可得,lowbit(i)=i&-i .
树状数组的前缀和存储方式
对于每一个求和数组\(c[i],c[i]\)的求和范围\(a[i-lowbit(i)+1]\)~\(a[i]\).
用一幅图可以形象直观的解释其存储方式:
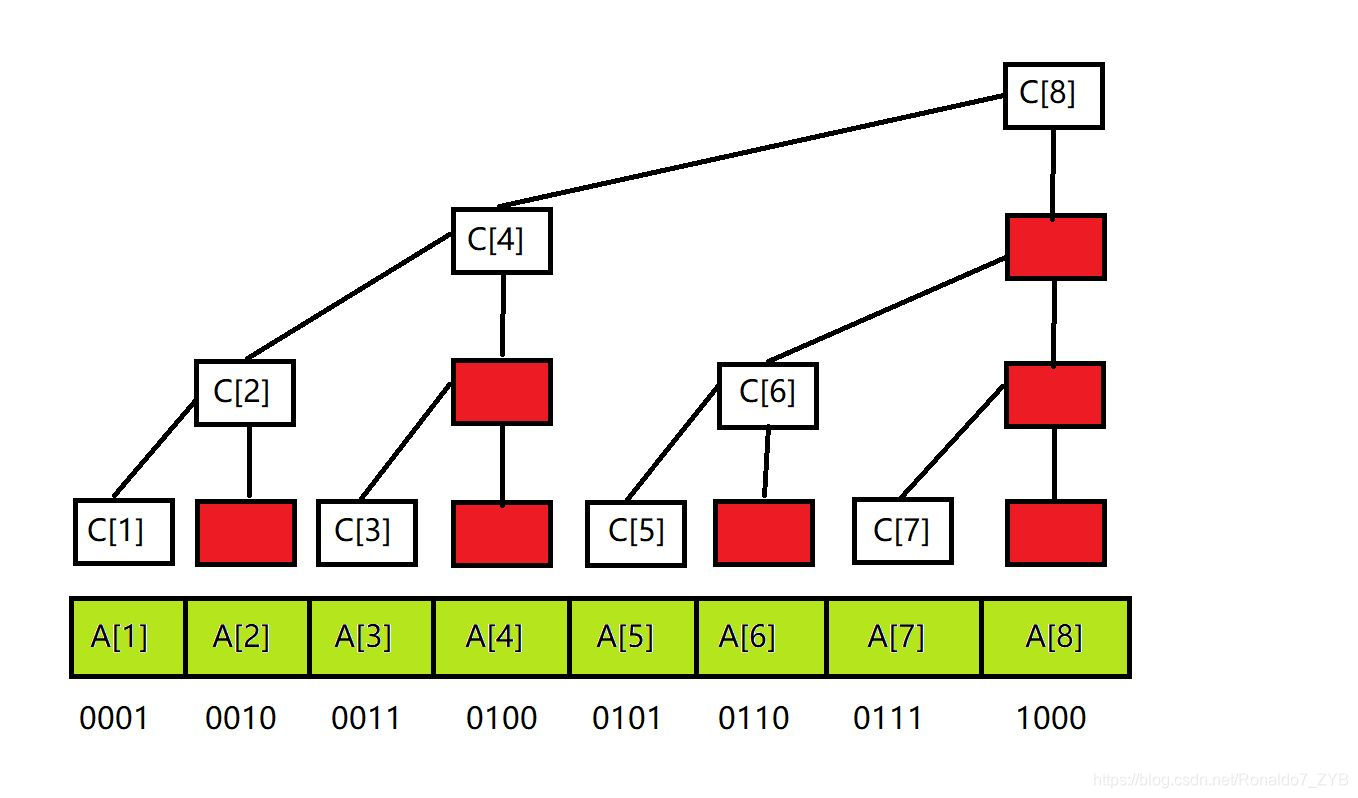
单点修改
对于\(add(x,val)\),表示\(a[x]\)加上了数值\(val\)。如何修改:
例如\(x=3\),需要修改的是\(3,4,8\)(若\(n=8\))
可见对于每一个修改的位置\(x\),下一个要修改的是\(x+lowbit(x).\)
即,\(3+lowbit(3)=4,4+lowbit(4)=8.\)
故得到代码如下:
void add(int x,int val)
{
for (int i=x;i<=n;i+=lowbit(i))
c[i]+=val;
return;
}区间查询
\(ask(x)\)表示要查询\(1\)~\(x\)的前缀和。
例如\(x=7,sum=c[7]+c[6]+c[4],\)
可见对于每一\(x\),下一步要累加的是\(c[x-lowbit(x)].\)
因此得到代码如下:
inline int ask(int x)
{
int ans=0;
for (int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}对于查询l到r区间的和,则\(sum=ask( r )-ask( l-1 ).\)
初始化
每一个\(c\)数组的求和范围是\(i-lowbit(i)+1\)~\(i,\)
可以利用最普通的前缀和直接求出\(1-i\)的和,
则\(c[i]=sum[i]-sum[i-lowbit(i)]\)。
模板例题——树状数组基本操作
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出包含若干行整数,即为所有操作2的结果。
注意n≤500000.
code:
#include<bits/stdc++.h>
using namespace std;
const int maxn=500000;
int n,m;
int a[maxn+10];
int c[maxn+10];
int sum[maxn+10];
#define lowbit(x) (x&-x)
void add(int x,int val)
{
for (int i=x;i<=n;i+=lowbit(i))
c[i]+=val;
return;
}
inline int ask(int x)
{
int ans=0;
for (int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=n;++i)
{
scanf("%d",a+i);
sum[i]=sum[i-1]+a[i];
}
for (int i=1;i<=n;++i) c[i]=sum[i]-sum[i-lowbit(i)];
for (int i=1;i<=m;++i)
{
int num,x,y;
scanf("%d%d%d",&num,&x,&y);
if (num==1) add(x,y);
else printf("%d\n",ask(y)-ask(x-1));
}
return 0;
} 差分——区间修改
已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数数加上x
2.求出某一个数的值
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x 含义:输出第x个数的值
注意n≤500000.
对于某一区间\(x~y\)加上\(k\),可以用一个数组b标记:\(b[x]\)加上\(k\),\(b[y+1]\)减去\(k\)。
仔细思考一下,其实十分巧妙:
对这个标记数组做前缀和,做到\(x\)及以后刚刚加上了k,但是做到\(y+1\)以后又减回去了。
因此我们只需要用树状数组去维护这个数组b的前缀和,对于操作\(2\)返回\(a[x]+ask(x)\)即可。
code:
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
#define LL long long
const LL maxn=500000;
LL n,m;
LL a[maxn+10];
LL c[maxn+10];
void add(LL x,LL val)
{
for (LL i=x;i<=n;i+=lowbit(i))
c[i]+=val;
return;
}
inline LL ask(LL x)
{
LL sum=0;
for (LL i=x;i>=1;i-=lowbit(i))
sum+=c[i];
return sum;
}
int main(void)
{
scanf("%lld%lld",&n,&m);
for (LL i=1;i<=n;++i) scanf("%lld",a+i);
for (LL i=1;i<=m;++i)
{
LL t;
scanf("%lld",&t);
if (t==1)
{
LL x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
add(x,k),add(y+1,-k);
}
if (t==2)
{
LL x;
scanf("%lld",&x);
printf("%lld\n",a[x]+ask(x));
}
}
return 0;
}备注
两道例题来自于洛谷\(P3374\)和\(P3368\).
欢迎指正!