机器学习 - 朴素贝叶斯（上）- 概率论基础

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/weixin_37352167/article/details/84861461

• 概率

  1. 联合概率，边缘概率 and 条件概率

     有事件 $A=\{a_1,a_2,…,a_m\}$ 和事件 $B=\{b_1,b_2,…,b_n\}$：

     $\bullet$ 条件概率 为 $P(B=b_j|A=a_i)$，表示在事件 $A=a_i$ 发生的条件下，事件 $B=b_j$ 发生的概率。

     $\bullet$ 联合概率 为 $P(A=a_i,B=b_j)$，表示事件 $A=a_i$ 和事件 $B=b_j$ 同时发生的概率。其中：

     $P(A,B)=\begin{cases} P(A)*P(B)，P(A) 与 P(B) 相互独立\\ P(A|B)P(B)=P(B|A)P(A)，P(A) 与 P(B) 不独立\\ \end{cases}$

     $\bullet$ 边缘概率 为 $P(A=a_i)$，表示在不考虑事件 $B$ 的情况，只需满足 $A=a_i$ 的概率。

  2. 先验概率 and 后验概率

     $\bullet$ 先验概率
     是指根据以往经验和分析得到的概率，如全概率公式，它往往作为"由因求果"问题中的"因"出现的概率。

     $\bullet$ 后验概率
     是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的"果"。先验概率与后验概率有不可分割的联系，后验概率的计算要以先验概率为基础。可通过贝叶斯公式求得。

     先验概率是通过现有历史资料计算得到，而不是根据有关自然状态的全部资料测定的。后验概率是在历史数据上又添加了新的资料，使用了有关自然状态更加全面的资料的基础上，对先验概率的修正。

  3. 全概率公式

     $\bullet$ 设 $Y=\{c_1,c_2,…,c_n\}$， $Y$ 包含有限或无限个事件，这些事件两两互斥且在每次试验中至少发生一个，它们将样本空间进行了划分，把具有这些性质的一组事件称为一个 完备事件组。
     
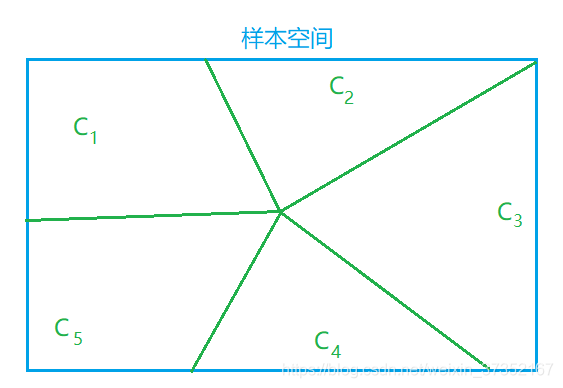
     图中，样本空间被完备事件组 $Y=\{c_1,c_2,c_3,c_4,c_5\}$ 划分成 5 各区域。

     ---

     $\bullet$ 设 $X=\{x_1,x_2,…,x_m\}$ 为另一个事件（ $X$ 同样也可把某一样本空间进行区域划分，在这里不予展示）。且在此假设 $Y=\{c_1,c_2,c_3,c_4,c_5\}$ 对事件 $X$ 的发生会产生影响。
     

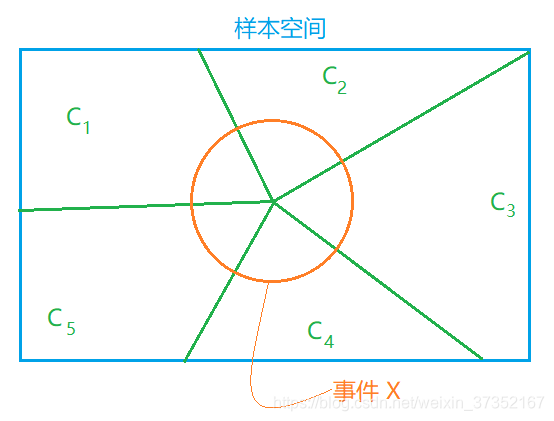
     全概率公式： $P(X)=\sum_{k}P(Y_k=c_k)P(X|Y=c_k)$

     在图所示的例子中， $P(X)=\sum_{k=1}^{5}P(Y=c_k)P(X|Y=c_k)$

     全概率公式的意义在于，当直接计算 $P(A)$ 较为困难，而 $P(Y=c_k)，P(X|Y=c_k)$的计算较为简单时，可以利用全概率公式计算 $P(A)$。将事件 $X$ 分解成若干个小事件，通过求每个小事件的概率，然后相加从而求得事件 $A$ 的概率。

     $P(X) = P(X,Y=c_1) + P(X,Y=c_2) + .... + P(X,Y=c_k)$
                  $=P(Y=c_1)P(X|Y=c_1) + P(Y=c_2)P(X|Y=c_2) + .... +P(Y=c_k)P(X|Y=c_k)$

  4. 贝叶斯公式

     贝叶斯公式可以用来计算后验概率。计算过程中使用条件概率与联合概率的关系，以及全概率公式。

     假设此时 $Y=\{c_1,c_2,…,c_n\}$

     根据 $P(X|Y)P(Y)=P(Y|X)P(X)$ （条件概率与联合概率的关系）

     得 $P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)}$

     又因 $P(X)=\sum_{k}P(Y_k=c_k)P(X|Y=c_k)$ （全概率公式）

     得 贝叶斯公式： $P(Y|X) = \frac{P(X|Y)P(Y)}{\sum_{k}P(Y_k=c_k)P(X|Y=c_k)}$

     其中，先验概率为 $P(Y)$ ，条件概率 $P(X|Y)$ 是“新的有关自然状态”的资料。利用贝叶斯公式求后验概率，是通过 $P(X|Y)$ 对先验概率 $P(Y)$ 进行修正。

  搞了一堆数学公式，比较抽象，下面正式进入机器学习中的 朴素贝叶斯，并用例子辅以说明。

  见 《机器学习 - 朴素贝叶斯（下）- 朴素贝叶斯分类器》