概率论第9记：随机变量的另外几个数字特征

这篇文章总结：矩、中心矩、分位数的概念

矩和中心距

设X是随机变量，如果E(X^k) k=1,2,…存在，则称它为X的k阶原点矩或k阶矩。
如果E{[X-E(x)]^k}存在，则称它为X的k阶中心矩。
显然，2阶中心距就是方差。

分位数

设连续型随机变量X的分布函数为F（x），概率密度函数为f（x），
1°对于任意正数α（0<α<1），称满足条件

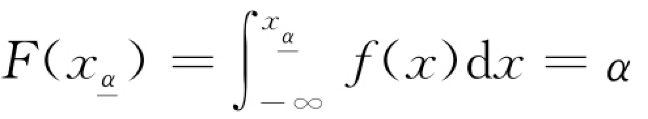
的数为此分布的α分位数或下α分位数.
2°对于任意正数α（0<α<1），称满足条件

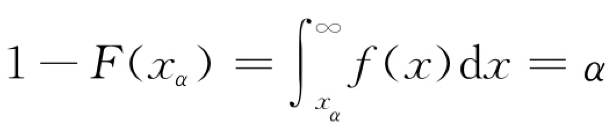
的数xα为此分布的上α分位数.
这里的xa，不要把a理解成随机变量下标，事实上也没有小数类型的下标，事实上就是一个满足积分值为a的数值而已，可以是1，2，3，4.23156等各种值，只是为了标明积分为a这个意义，x后面下缀一个a，而且分位数和a之间除了这个积分关系，没有其他关系。
特别的：如果xa=0.5,a也等于0.5那么xa称为中位数。刚好在这个点，把积分区间2等分。
类似的还有四分位数，百分位数。
上下分位数有如下关系：

$x_{\underline a}=x_{1-a}$
$x_{a}=x_{\underline {1-a}}$
下面举一个例题：
设随机变量X服从指数分布，其分布函数为

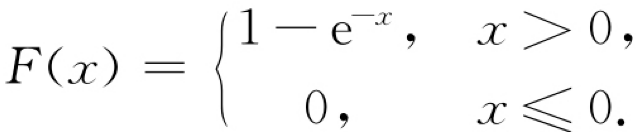
求中位数x0.5及上分位数x0.25.
解
（注意这里是连续型随机变量的分布函数，不是概率密度函数，所以不需要积分运算）
由F（x0.5）=1-e-x0.5=0.5，得e-x0.5=0.5，故中位数x0.5=-ln0.5=0.69.由F（x0.25）=1-e-x0.25=0.25，得e-x0.25=0.75.故x0.25=-ln0.75=0.29.

变异系数

设X是随机变量，如果 $\frac{\sqrt{D(X)}}{E(X)}$存在，记作(CV)_x，称之为X的变异系数。
变异系数通常用来衡量X取值的分散程度，作用和方差是一样的。