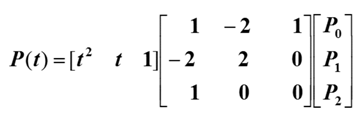相关基础理论知识
我们根据平面上的一些离散点绘制出一条近似曲线。如果曲线通过所有点,称为插值;如果曲线不一定通过点,而是以某种方式逼近这些点,称为拟合。
构造拟合曲线,通常有以下几种方法:
(1)最小二乘法;
(2)分段拟合法;
(3)…
最小二乘法
根据解的存在情况,线性方程可以分为:
- 有唯一解的恰定方程组;
- 解不存在的超定方程组;
(Ax=b,A为n×m矩阵,如果A列满秩,且n>m,方程组没有精确解,常用于数据拟合); - 有无穷多解的欠定方程组;
(Ax=b,A为n×m矩阵,如果A行满秩,且n<m);
在MATLAB中求解超定方程,有以下几种方法:
- 左除是建立在奇异值分解基础之上得到最小二乘法的解,因此最可靠;
x=A\b;
- 最小二乘法求解;
x=lsqnonneg(A,b);
- 广义逆,解不一定满足Ax=b,x只是最小二乘意义上的解;
x=pinv(A);
广义逆(伪逆矩阵)
广义逆法(伪逆矩阵)是建立在对原超定方程直接进行 householder变换的基础上,其算法可靠性稍逊与(SVD)奇异值求解,但速度较快;以B=pinv(A)为例,函数返回矩阵A的伪逆矩阵。如果矩阵A是可逆(非奇异)的,那么pinv(A)与inv(A)的结果是一样的,而且pinv比inv效率低。但如果矩阵A是非方阵或奇异矩阵,则inv(A)不存在,但pinv(A)仍然存在,并表现出一些与逆矩阵类似的性质。
【定义】
令A是任意m x n矩阵,若G满足下述条件(Moore-penrose条件),称矩阵G是A的广义逆矩阵:
(1)GAG = G;
(2)AGA = A;
(3)AG为hermitian矩阵,即(AG)^H=AG;
(4)GA为hermitian矩阵,即(GA)^H=GA;
【测试】
在Matlab中,用以下几种方式求逆:
(1)直接求解:InvA = inv(A’*A)*A’; %求导,令导数为0,结果如下: InvA=(ATA)-1AT
(2)SVD分解:[U,Λ,V]=svd(A)
(3)QR分解:[Q,R]=qr(A)
(4)LU分解:[L,U]=lu(A)
a=[1 2 3; 4 5 6; 23 3 6];
b=inv(a);
c=pinv(a);
[U,D,V]=svd(a);
D1=[1/24.8393,0,0;0,1/6.9174,0;0,0,1/0.4016];
U1=U';
d =V*D1*U1;
e=inv(a'*a)*a';
结果:

矩阵分解
由上面例子可知,我们可以通过矩阵分解来求逆矩阵,接下来介绍几种矩阵分解的方式:
-
特征值分解(Eigen Value Decomposition,EVD)
特征值分解,是指将矩阵分解为由特征值和特征向量表示的矩阵之积的方法。由(λ I - A)v=0(λ 为N 阶方阵A的特征值,v为特征值 λ 对应的特征向量)求解特征值和特征向量:
(1)特征值:det | λ I - A | = 0(特征多项式),可以得到:
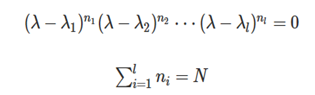
这样,我们便可以得到矩阵A的l种不同的特征值,每种特征值有ni个重复,共有N个特征值。
(2)特征向量:对于单根特征值,(λi I - A)vi =0,即可求得该特征值对应的特征向量;对于有重根的特征值,可用以下公式依次迭代求解:
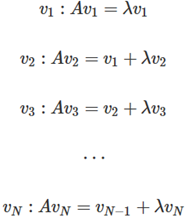
这样,特征分解将矩阵分解为如下形式:A=QΛQ-1;若无重根,Λ=diag(λ1,λ2,…,λn),若有重根,Λ为Jordan标准型。这里的Q是以特征向量为列向量的N x N矩阵。 -
Householder变换法(QR Factorization,QR分解)
这是目前求一般矩阵全部特征值的最有效并广泛应用的方法,精度高于伪逆法。一般矩阵先经过正交相似变化成为Heisenberg矩阵,然后再应用QR方法求特征值和特征向量。
A=QR (其中:A为m x n的矩阵,n>=m,Q为m×m的正交矩阵,R为m×n的上三角矩阵),我们称其为A的QR分解。 -
奇异值分解(singular value decomposition,SVD)
对于矩阵A ϵ Fm x n,A=UΛVT,其中,U ϵ Fm x m酉矩阵,被称为左奇异向量;Λ ϵ Fm x n的半正定对角矩阵,Λ 对角线上的元素 λi为原矩阵A的奇异值;V T ϵ F n×n 是V 的共轭转置,被称为右奇异向量,这样的分解称为奇异值分解。
Matlab样条工具箱(Curve Fitting Toolbox)与曲线拟合
样条函数可分为4类:cs* 三次样条、系数为t^n 的pp* 分段多项式样条、系数为基函数B_n^i(t)的sp* B样条、 rp* 有理B样条。样条操作包括:函数操作(求值,算术运算,求导求积分等)、节点操作(节点重数的调节,设定,修改等)。
- 导入数据,打开工具箱选择合适的模型拟合
代码:
x0=data(1,:);
y0=data(2,:);
cftool;
结果:
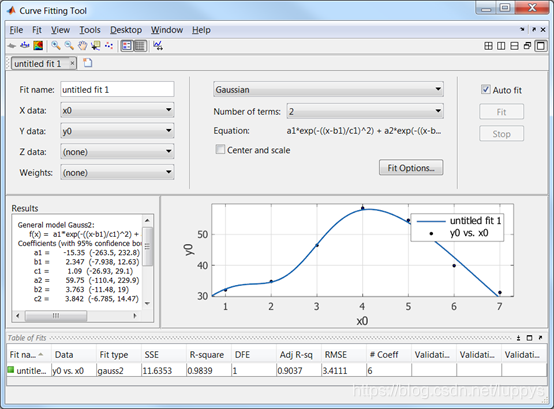
2. 样条工具箱函数
(1). 三次样条函数
csapi 插值生成三次样条函数
csape 生成给定约束条件下的三次样条函数
csaps 平滑生成三次样条函数
cscvn 生成一条内插参数的三次样条曲线
getcurve 动态生成三次样条曲线
(2). 分段多项式样条函数
ppmak 生成分段多项式样条函数
ppual 计算在给定点处的分段多项式样条函数值
(3). B样条函数
spmak 生成B样条函数
spcrv 生成均匀划分的B样条函数
spapi 插值生成B样条函数
spap2 用最小二乘法拟合生成B样条函数
spaps 对生成的B样条曲线进行光滑处理
spcol 生成B样条函数的配置矩阵
(4). 有理样条函数
rpmak 生成有理样条函数
rsmak 生成有理样条函数
(5). 样条操作函数
fnval 计算在给定点处的样条函数值
fmbrk 返回样条函数的某一部分(如断点或系数等)
fncmb 对样条函数进行算术运算
fn2fm 把一种形式的样条函数转化成另一种形式的样条函数
fnder 求样条函数的微分(即求导数)
fndir 求样条函数的方向导数
fnint 求样条函数的积分
fnjmp 在间断点处求函数值
fnplt 画样条曲线图
fnrfn 在样条曲线中插入断点。
fntlr 生成tarylor系数或taylor多项式
(6). 样条曲线端点和节点处理函数
augknt 在已知节点数组中添加一个或多个节点
aveknt 求出节点数组元素的平均值
brk2knt 增加节点数组中节点的重次
knt2brk 从节点数组中求得节点及其重次
knt2mlt 从节点数组中求得节点及其重次
sorted 求出节点数组的元素在另一节点数组中属于第几个分量
aptknt 求出用于生成样条曲线的节点数组
newknt 对分段多项式样条函数进行重分布
optknt 求出用于内插的最优节点数组
chbpnt 求出用于生成样条曲线的合适节点数组
样条线拟合
spline函数(piecewise polynomial function)
特点:
设样条函数为S;导入数据点为:knots(结)(k组数据,则有k个结,k-1段,k-1个多项式函数);相邻两个knots之间分段定义多项式函数Si(i=0,1,……,k-1),则S=S1+ S2+……+Sk-1;
>>x0=data(1,:);
>>y0=data(2,:);
>>x1=1:0.1:7;%设置插值的自变量
>>n=spline(x0,y0);%返回函数的结构体信息
>>y1=spline(x0,y0,x1);%返回插值计算的函数值
>>plot(x0,y0,'ro');
>>plot(x1,y1,'r-');
>>num=4;
>>x=0:0.1:7;
%最大值所在方程函数
>>y=f2.coefs(num,1).*(x-num).^3+f2.coefs(num,2).*(x-num).^2+f2.coefs(num,3).*(x-num)+f2.coefs(num,4); >>x_solve=x(find(y==max(y)));
结果:
n =
form: 'pp' %样条函数类型
breaks: [1 2 3 4 5 6 7] %分段区间节点矩阵
coefs: [6x4 double] %各分段区间上的插值多项式系数矩阵
pieces: 6 %分段数
order: 4 %项式阶数
dim: 1 %矩阵维度
x_solve =
4.3000
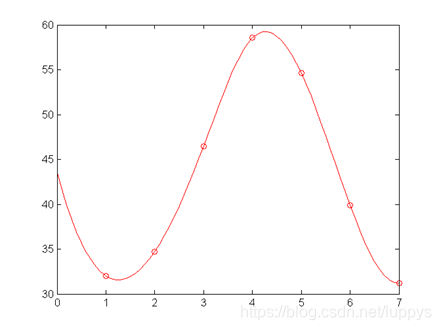
polyfit(x,y,N)函数
特点:对数据x,y拟合N阶多项式
>>x0=data(1,:);
>>y0=data(2,:);
>>x1=1:0.1:n;
>>f1=polyfit(x0,y0,2); %polynomial fitting
>>y2=polyval(f1,x1); %Calculate dependent variable
>>plot(x1,y2,'g-');
结果:

二次B样条曲线
特点:已知三个平面离散点就可以定义二次抛物线段,多于3个离散点,则采用二次B样条曲线分段拟合。
设有n+1个离散点,记为Pi(i=0,1,…,n)
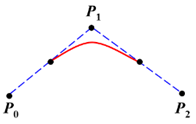
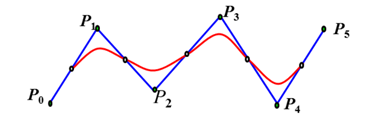
矩阵形式为:
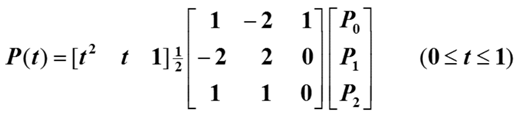
三次B样条曲线
矩阵形式为:
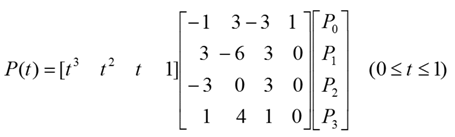
二次Beier曲线
矩阵形式为: