万事开头难,所以我们先研究这个最简单的滤波器传递函数:
H
(
s
)
=
1
1
+
s
H(s) = \frac{1}{1+s}
H ( s ) = 1 + s 1
这是一个最简单的1阶低通滤波器的传递函数,当s=0时, |H(s)|=1;当s=
∞
\infty
∞
H
(
j
Ω
)
=
1
1
+
j
Ω
H(j\Omega) = \frac{1}{1+j\Omega}
H ( j Ω ) = 1 + j Ω 1
Ω
\Omega
Ω
2
\sqrt 2
2
Ω
=
1
\Omega=1
Ω = 1
Ω
\Omega
Ω
π
\pi
π
π
\pi
π
H
(
s
)
=
Ω
c
Ω
c
+
s
H(s) = \frac{\Omega_c}{\Omega_c+s}
H ( s ) = Ω c + s Ω c
Ω
c
\Omega_c
Ω c
π
\pi
π
f
c
f_c
f c
用s=
1
s
\frac{1}{s}
s 1
H
(
s
)
=
Ω
c
s
Ω
c
s
+
1
H(s) = \frac{\Omega_c s}{\Omega_c s+1}
H ( s ) = Ω c s + 1 Ω c s
∞
\infty
∞
Ω
c
\Omega_c
Ω c
π
\pi
π
f
c
f_c
f c
Ω
h
\Omega_h
Ω h
1
Ω
c
\frac{1}{\Omega_c}
Ω c 1
Ω
c
\Omega_c
Ω c
1
Ω
h
\frac{1}{\Omega_h}
Ω h 1
π
\pi
π
f
h
f_h
f h
f
h
f_h
f h
1
2
π
Ω
h
\frac{1}{2\pi\Omega_h}
2 π Ω h 1
H
(
s
)
=
s
s
+
Ω
h
H(s) = \frac{s}{s+\Omega_h}
H ( s ) = s + Ω h s
Ω
h
\Omega_h
Ω h
低通变带通要比之前变高通复杂了,替换公式
s
=
s
2
+
Ω
m
2
B
W
s = \frac{s^2+\Omega_m ^2}{BW}
s = B W s 2 + Ω m 2
H
(
s
)
=
B
W
s
2
+
Ω
m
2
+
B
W
H(s) = \frac{BW}{s^2+\Omega_m ^2+BW}
H ( s ) = s 2 + Ω m 2 + B W B W
高通变带阻,一样的替换公式,
s
=
s
2
+
Ω
c
2
B
W
s = \frac{s^2+\Omega_c ^2}{BW}
s = B W s 2 + Ω c 2
H
(
s
)
=
s
s
+
1
H(s) = \frac{s}{s+1}
H ( s ) = s + 1 s
H
(
s
)
=
s
2
+
Ω
m
2
s
2
+
Ω
m
2
+
B
W
H(s) = \frac{s^2+\Omega_m ^2}{s^2+\Omega_m ^2+BW}
H ( s ) = s 2 + Ω m 2 + B W s 2 + Ω m 2
假设我们需要为外放输出的数字音频作一个高通滤波器,截止频率在400Hz,采样频率48000Hz,第一章我们已经有了一个原型:
H
(
s
)
=
s
s
+
1
H(s) = \frac{s}{s+1}
H ( s ) = s + 1 s
ω
c
=
2
π
f
f
s
\omega_c =\frac{2\pi f}{f_s}
ω c = f s 2 π f
数字和模拟频率的转换关系:
Ω
c
=
ω
c
T
\Omega_c = \frac{\omega_c}{T}
Ω c = T ω c
Ω
c
=
2
T
tan
ω
c
2
\Omega_c = \frac{2}{T}\tan{\frac{\omega_c}{2}}
Ω c = T 2 tan 2 ω c
ω
c
=
2
π
f
f
s
=
π
60
≈
0.05236
\omega_c =\frac{2\pi f}{f_s}=\frac{\pi}{60}\approx 0.05236
ω c = f s 2 π f = 6 0 π ≈ 0 . 0 5 2 3 6
Ω
c
=
ω
c
T
≈
0.05236
T
\Omega_c = \frac{\omega_c}{T}\approx \frac{0.05236}{T}
Ω c = T ω c ≈ T 0 . 0 5 2 3 6
Ω
c
=
2
T
tan
ω
c
2
≈
0.05236
T
\Omega_c = \frac{2}{T}\tan{\frac{\omega_c}{2}} \approx \frac{0.05236}{T}
Ω c = T 2 tan 2 ω c ≈ T 0 . 0 5 2 3 6
s
=
s
Ω
c
{s=\frac{s}{\Omega_c}}
s = Ω c s
H
(
s
)
=
s
Ω
c
+
s
=
s
T
0.05236
+
s
T
H(s) = \frac{s}{\Omega_c+s}= \frac{sT}{0.05236 +sT}
H ( s ) = Ω c + s s = 0 . 0 5 2 3 6 + s T s T
s
=
2
T
z
−
1
z
+
1
=
2
T
1
−
z
−
1
1
+
z
−
1
s = \frac{2}{T} \frac{z-1}{z+1}=\frac{2}{T} \frac{1-z^{-1}}{1+z^{-1}}
s = T 2 z + 1 z − 1 = T 2 1 + z − 1 1 − z − 1
H
1
(
z
)
=
1
−
z
−
1
1.02618
−
0.97371
z
−
1
H_1(z) = \frac{1-z^{-1}}{1.02618-0.97371z^{-1}}
H 1 ( z ) = 1 . 0 2 6 1 8 − 0 . 9 7 3 7 1 z − 1 1 − z − 1
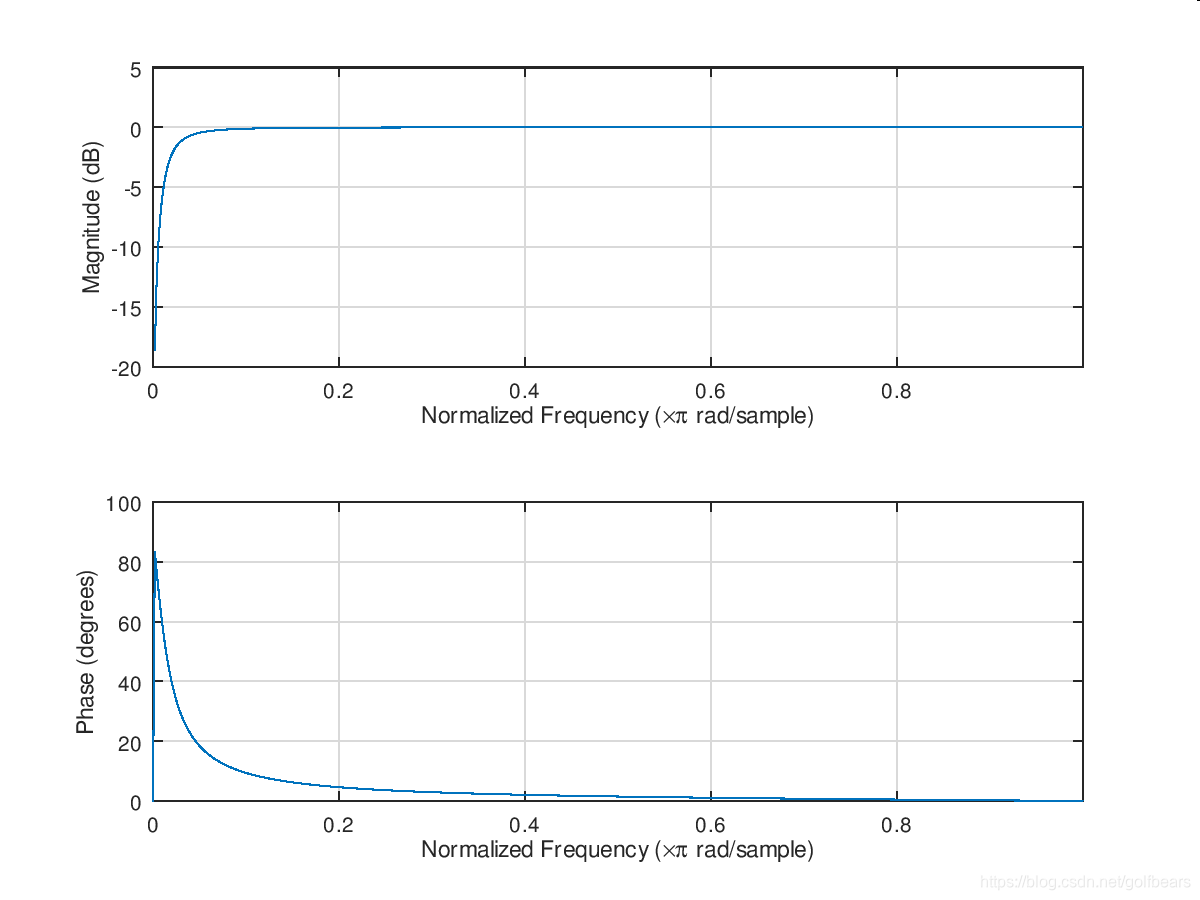
利用Octave开源的工具,几乎可以替换Matlab,
H
(
z
)
H(z)
H ( z )
我们用最简单的模拟低通滤波器推导出一个简单的数字高通滤波器,基本满足假设的使用要求。本文主要参考了《Real-Time Digital Signal Processing Fundamentals, Implementations