后缀数组SA

引言

蒟蒻死磕了一周才算是对后缀数组入了门
后缀数组一般有两种求法
倍增法 $O(nlogn)$ 和 DC3算法 $O(n)$
DC3法编程复杂度极高，空间开销也大，所以这里只讲一下倍增法，~~其实是蒟蒻并不会DC3~~

参考资料——罗穗骞《后缀数组——处理字符串的有力工具》

学习后缀数组前
你需要对基数排序有一定的了解
了解了基数排序之后我们从下面的问题引入后缀数组

Q：读入一个长度为 n 的字符串，把这个字符串的所有非空后缀按字典序从小到大排序
比如下图这样
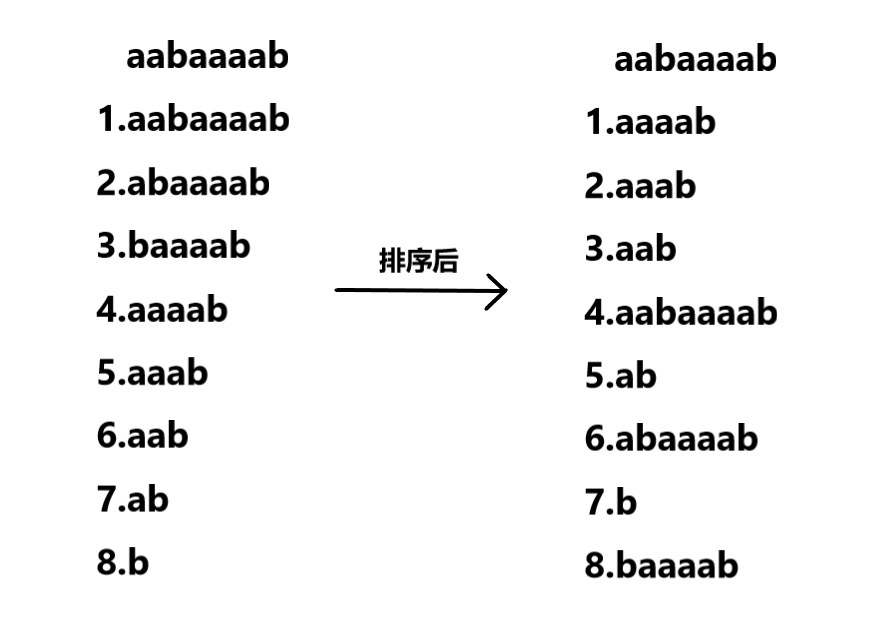
在这里插入图片描述

算法分析

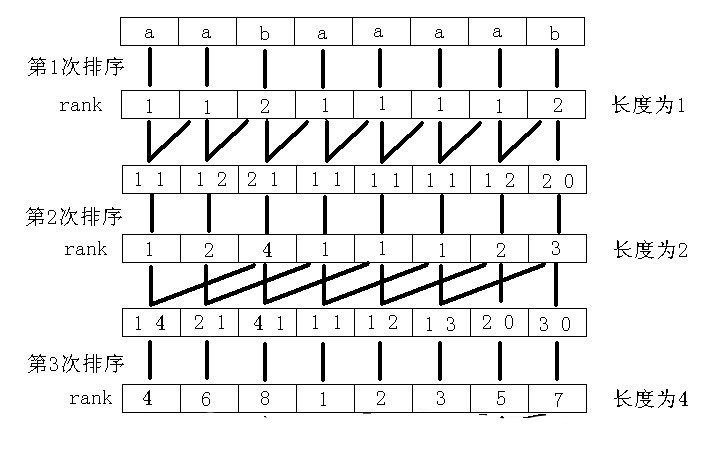
先丢上一张图解(图片来源–2009集训队论文–《后缀数组——处理字符串的有力工具》)
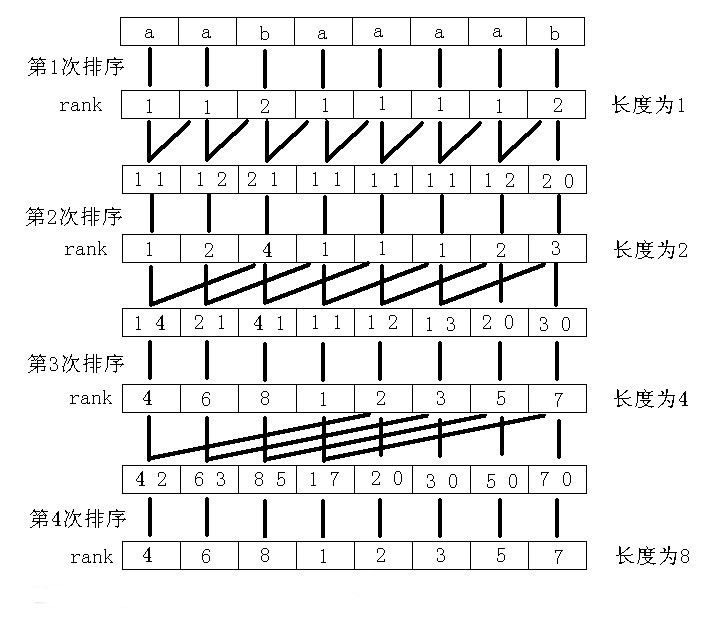
在这里插入图片描述
~~我知道你们一定看得一脸懵逼，反正我第一次就是这样~~
那么就先讲解一下这个排序的大致思路

以下简记从第 $i$ 位开始的后缀为后缀 $i$
一开始先对每个后缀的第一个字符排序
然后我们发现后缀 $i$ 的第2个字符就是后缀 $i+1$ 的第1个字符
而每个后缀的第1个字符已经排好序，于是我们可以利用这一点对每个后缀的前两个字符排序
这时候我们再次发现后缀 $i$ 的第3、4个字符就是后缀 $i+2$ 的前两个字符
于是再次利用这点对每个后缀的前四个字符排序
如此反复，排序前1个字符、前2个、前4个、前8个，最后排完前n个字符便完成了排序
这里很明显用到了倍增思想

直接描述可能还是不能很好的帮助理解
我们再以上图为例逐步解释

先对每个后缀的第一个字符排序
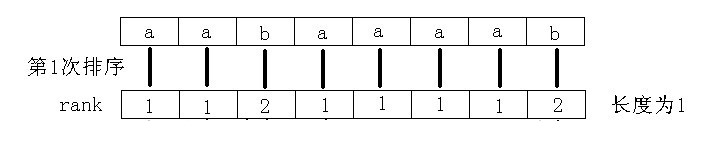
在这里插入图片描述

接着我们要巧妙地利用上一轮的rank来排序每个后缀的前2个字符
对于每个后缀的前2个字符，我们用一个两位的p进制数来表示(p为上一轮不同的rank数)
由于后缀 $i$ 的第2个字符就是后缀 $i+1$ 的第1个字符
所以我们用来表示后缀 $i$ 前两个字符的k进制数就是
上一轮后缀 $i$ 第1个字符的rank作为最高位，后缀 $i+1$ 第1个字符的rank作为第二位
不足的补0

这样利用基数排序，先比较最高位，也就相当于先按每个后缀第一个字符排序
再比较第二位，即如果有第一个字符相同的则再比较第二个字符rank大小
从而对后缀前两个字符完成了排序
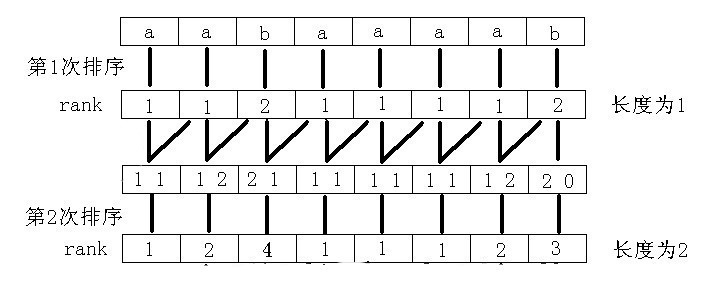
在这里插入图片描述

此时我们得到了每个后缀前两个字符的rank
同理后缀 $i$ 的第3、4个字符就是后缀 $i+2$ 的前两个字符
于是我们还可以用相同的方法对每个后缀的前四个字符排序

对于每个后缀的前4个字符，还是用一个两位的p进制数来表示(p为上一轮不同的rank数)
而这次的组成就是上一轮后缀 $i$ 前两个字符的rank作为最高位，后缀 $i+2$ 前两个字符的rank作为第二位
同样利用基数排序完成后缀前四个字符的排序
在这里插入图片描述

同理完成前四个字符的排序后再次构造的两位p进制数为
上一轮后缀 $i$ 前四个字符的rank作为最高位，后缀 $i+4$ 前四个字符的rank作为第二位
再次排序即完成前八个字符的排序
在这里插入图片描述
到这里排序完成

再次用形式化一些的语言描述以下这个过程
假设当前我们已经知道每个后缀前k个字符的排序结果(rank)
由于后缀 $i$ 的第 $i+k$ ~ $i+2k-1$ 个字符与后缀 $i+k$ 的前 $k$ 个字符相同
所以利用这点将后缀 $i$ 的前k个字符的rank作为一个进制数的最高位
后缀 $i+k$ 的前 $k$ 个字符的rank作为这个进制数的第二位
将得到的n个数利用基数排序排序后即得到了每个后缀前 $2k$ 个字符的rank

如此利用倍增每次排序长度翻倍，排序总次数为 $logn$
每次排序复杂度为 $O(m)$ (m为当前排序时已经出现的不同的排名个数)
总时间复杂度为 $O(mlogn)$

代码实现

了解了上述算法的思路后考虑一下代码实现
似乎上面的算法并没有用到什么后缀数组啊，我们在这里开始引入这个概念

$rak[i]$ ：后缀 $i$ (前k个字符)的排名
$sa[i]$ ：当前排名为 $i$ 的后缀(前k个字符)开始的位置 (即后缀数组)
$tp[i]$ ：与sa或rak相同，辅助基数排序，具体用法下面解释
$tax[i]$ ：基数排序用的桶

先丢上一个完整的代码

//省去了数组定义之类乱七八糟的东西
void rsort()
{
    for(int i=0;i<=m;++i) tax[i]=0;
    for(int i=1;i<=n;++i) tax[rak[i]]++;
    for(int i=1;i<=m;++i) tax[i]+=tax[i-1];
    for(int i=n;i>=1;--i) sa[tax[rak[tp[i]]]--]=tp[i];
}

void ssort()
{
    m=127;
    for(int i=1;i<=n;++i)
    rak[i]=a[i],tp[i]=i;
    
    rsort(); 
    for(int k=1;k<=n;k<<=1)
    {
        int p=0;
    	for(int i=n-k+1;i<=n;++i) tp[++p]=i;
        for(int i=1;i<=n;++i) if(sa[i]>k) tp[++p]=sa[i]-k;
        
    	rsort(); 
    	swap(rak,tp);
    	rak[sa[1]]=p=1;
    	for(int i=2;i<=n;++i)
        rak[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+k]==tp[sa[i-1]+k])?p:++p;
        if(p>=n)break;
    	m=p;
    }
    return;
}

int main()
{
    scanf("%s",&ss); n=strlen(ss);
    for(int i=0;i<n;i++) a[i+1]=ss[i];
    
    ssort();
    for(int i=1;i<=n;i++) 
    printf("%d ",rak[i]);
    return 0;
}

直接看代码还是会很难理解
因为具体的实现与上面的算法描述还是有一些出入的，所以我们逐行解释

m=1024;
for(int i=1;i<=n;++i)
rak[i]=a[i],tp[i]=i;
rsort();

m用于优化基数排序，代表当前不同的排名个数

a数组以ASCII码形式保存了字符串
第一次排序时直接利用ASCII码即可，所以 $rak[i]=a[i]$

我们先暂时不讨论基数排序如何实现
先记住这里 $rsort()$ 之后我们就得到了每个后缀第一个字符的sa数组

第一次排序完成
在这里插入图片描述

for(int k=1;k<=n;k<<=1)

倍增长度枚举

int p=0;
for(int i=n-k+1;i<=n;++i) tp[++p]=i;
for(int i=1;i<=n;++i) if(sa[i]>k) tp[++p]=sa[i]-k;

p相当于一个计数器，接下来会有不同的用途
当前sa数组保存了上述算法中对该轮排序需要用到的那个二位进制数的最高位排序的结果
tp则是第二位

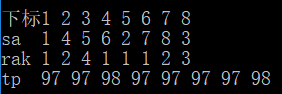
在这里插入图片描述

例如这一轮排序
只比较两两最高位大小情况，那么排名依次是 1 1 2 1 1 1 1 2
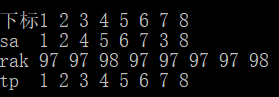
根据sa的定义(排名为 $i$ 的位置)即得到下图
tp也是如此，即第二位排名依次是2 3 2 2 2 2 3 1，对应到tp如下图所示

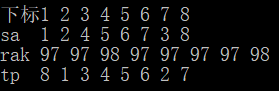
在这里插入图片描述

根据图解不难得到tp的求法

for(int i=n-k+1;i<=n;++i) tp[++p]=i;

即 $i+k$ 已经超过范围，第二位直接补0，那么排名自然在最前面 (排名相同就按出现先后)

for(int i=1;i<=n;++i) if(sa[i]>k) tp[++p]=sa[i]-k;

对于没有超出范围的，直接向前挪动k位即可

利用rak和tp再次排序得到新的sa，即长度翻倍后的sa数组
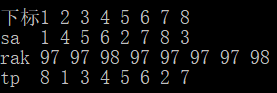
在这里插入图片描述

接下来得到了长度翻倍后的sa数组，rak却还没更新
于是利用上一轮的rak(长度未翻倍)和该轮的sa(长度翻倍后)来更新rak

swap(rak,tp);
rak[sa[1]]=p=1;
for(int i=2;i<=n;++i)
rak[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+k]==tp[sa[i-1]+k])?p:++p;

由于tp数组此时没用，所以直接交换，接下来tp表示上一轮的rak

rak[sa[1]]=p=1;

根据rak和sa的定义，不难得出 $rak[sa[i]]=sa[rak[i]]=i$ 这个结论

for(int i=2;i<=n;++i)
rak[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+k]==tp[sa[i-1]+k])?p:++p;

由于每个后缀的前k个字符可能有相同的情况，所以还要判重，令一样的子串rank也一样
在这里插入图片描述

if(p>=n)break;
m=p;

此时计数器p保存了不同的排名个数，如果已经有n个不同的排名就不用继续排了
m更新为当前不同排名数，优化基数排序

到这里已经比较详细的解释了每个后缀前两个字符排序完成的过程
如果还是没理解可以再自己观察一下接下来每次排序后各个数组的情况
对倍增的过程解释到这里，接下来再看看基数排序

void rsort()
{
    for(int i=0;i<=m;++i) tax[i]=0;
    for(int i=1;i<=n;++i) tax[rak[i]]++;
    for(int i=1;i<=m;++i) tax[i]+=tax[i-1];
    for(int i=n;i>=1;--i) sa[tax[rak[tp[i]]]--]=tp[i];
}

第一行清空桶
第二行记录每个排名出现的次数
第三行求前缀和
第四行@#￥%……&*（）

$tp[i]$ 所有进制数第二位排名为 $i$ 的那个数是第几个
$rak[tp[i]]$ 找到他最高位的排名
$tax[rak[tp[i]]]$ 看有多少个排名出现在这个排名之前
$sa[tax[rak[tp[i]]]--]$ 用它前面的个数更新sa
倒叙保证了排序完成后第二位的有序性

对代码思路也做一个形式化一些的总结

假设当前以求得每个后缀前k个字符排序结果，即得到了前k个字符的rak和sa
现在需要求长度为2k的排序结果
根据当前sa求出表示每个进制数第二位排序结果的tp
利用长度为k的rak和tp求出长度为2k的sa
用长度为k的rak和长度为2k的sa求出长度为2k的rak

后缀数组の应用

后缀数组求出来好像一般也干不了啥
但是根据sa可以求出一个更强力的height数组

$lcp(i,j)$ ：后缀 $i$ 与后缀 $j$ 的最长公共前缀
$height[i]：lcp(sa[i],sa[i−1])$ ，即排名为i的后缀与排名为i−1的后缀的最长公共前缀
$H[i]：height[rak[i]]$ ，即后缀 $i$ 与它前一名的后缀的最长公共前缀

如果直接按height[1],height[2],height[3]…顺序计算，复杂度将可能达到 $O(n^2)$
为了快速计算height数组，我们需要用到H数组的一个性质

$H[i]>=H[i-1]+1$

证明

设后缀 $k$ 是后缀 $i-1$ 前一名的后缀，则它们的lcp长度是 $H[i-1]$
因为后缀 $k+1$ 将排在后缀 $i$ 的前面
且后缀 $k+1$ 和后缀 $i$ 的lcp长度是 $H[i-1]-1$
所以后缀 $i$ 和在它前一名的后缀的lcp至少是 $H[i-1]-1$

按照 $H[1],H[2],……,H[n]$ 的顺序计算，并利用 H 数组的性质
时间复杂度可以降为 $O(n)$

//字符串从数组下标1开始储存
void getH()
{
	int k=0;
	for(int i=1;i<=n;++i)
	{
		if(k) k--;//长度至少时H[i]-1
		int j=sa[rak[i]-1];//后缀i前一名后缀的位置
		while(ss[i+k]==ss[j+k]) k++;//不断向后扩展
		height[rak[i]]=k;
	}
}