最近刷了不少题都是在01背包问题的基础上改编过来的。今天总结一下。
其实DP和DFS本质上就是一种遍历,只不过是带记忆的遍历罢了
只要用DP能做的用递归一定能做,即只要拿到了迭代式就可以用递归暴力破解,复杂度一般为O(2^n)
先回顾一下DP问题的解法:
1.先要搞清楚用一维数组还是二维,有几个限制条件就用几维。
2.搞清楚dp[i],dp[i][j]存放的值的确切含义,以01背包问题为例,dp[i][j]存放当i,j一定时的最优状态。
3.考虑第二个for循环是正序还是逆序,这取决于遍历的过程种要不要用到前面的值。
4.dp[i] = 取最优 {子状态1 ,子状态2,... ,子状态k}。以01背包问题为例子,dp[i] = max {取i, 不取i}

01背包问题这两种解法,一种用DP,一种用DFS。
一、DP
dp[i]代表:从前i个商品中挑选
dp[j]代表:重量不超过j
dp[i][j]代表:价值的最大值
合起来dp[i][j]就代表:从前i个商品中挑选重量不超过j的的物品时,价值的最大值。
就会有下面的状态转移方程和表格:
if j >=w[i]:
sum_v[i][j] = max{sum_v[i-1][j-w[i]] + v[i], sum_v[i-1][j]}
else:
sum_v[i][j] = sum_v[i-1][j]
01背包的本质就是在物品的不断遍历下和在容量的不断递增下,寻找当容量一定时 取第i个物品的状态和不取第i个物品的状态哪个最优。
有几个限制条件就可以构造几重for循环。
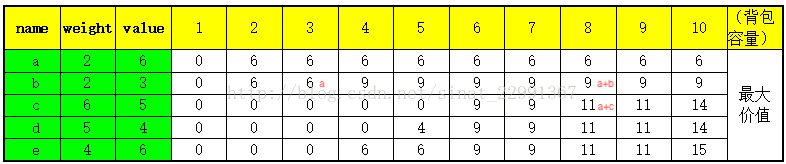

看这里:可以发现0-1背包的状态转移方程 dp[i][j] = max{dp[i-1][j-w[i]]+v[i],dp[i-1][j]}的特点,当前状态仅依赖前一状态的剩余体积与当前物品体积v[i]的关系。根据这个特点,我们可以将dp降到一维即dp[j] = max{dp[j],dp[j-w[i]]+v[i]}。从这个方程中我们可以发现,有两个dp[j],但是要区分开。等号左边的dp[j]是当前i的状态,右边中括号内的dp[j]是第i-1状态下的值。
所以为了保证状态的正确转移,我们需要先更新等号左边中的dp[j](当前状态的dp[j])。
此时数组长度为背包容量+1

void FindMaxBetter()//优化空间后的动态规划
{
int i,j;
for(i=1;i<=number;i++)
{
for(j=capacity;j>=0;j--)
{
if(B[j]<=B[j-w[i]]+v[i] && j-w[i]>=0 )//二维变一维
{
B[j]=B[j-w[i]]+v[i];
}
}
}
}
http://www.cnblogs.com/Christal-R/p/Dynamic_programming.html