During the kindergarten days, flymouse was the monitor of his class. Occasionally the head-teacher brought the kids of flymouse’s class a large bag of candies and had flymouse distribute them. All the kids loved candies very much and often compared the numbers of candies they got with others. A kid A could had the idea that though it might be the case that another kid B was better than him in some aspect and therefore had a reason for deserving more candies than he did, he should never get a certain number of candies fewer than B did no matter how many candies he actually got, otherwise he would feel dissatisfied and go to the head-teacher to complain about flymouse’s biased distribution.
snoopy shared class with flymouse at that time. flymouse always compared the number of his candies with that of snoopy’s. He wanted to make the difference between the numbers as large as possible while keeping every kid satisfied. Now he had just got another bag of candies from the head-teacher, what was the largest difference he could make out of it?
The input contains a single test cases. The test cases starts with a line with two integers N and M not exceeding 30 000 and 150 000 respectively. N is the number of kids in the class and the kids were numbered 1 through N. snoopy and flymouse were always numbered 1 and N. Then follow M lines each holding three integers A, B and c in order, meaning that kid A believed that kid B should never get over c candies more than he did.
Output one line with only the largest difference desired. The difference is guaranteed to be finite.
2 2 1 2 5 2 1 4Sample Output
5Hint
题意:有n个人m条信息,每条信息有a,b,c表示b最多比a多c颗糖果即b-a>=c,问n最多比1多多少颗糖果。
解题思路:
不会。
差分约束最短路方法求解。
差分约束:https://blog.csdn.net/my_sunshine26/article/details/72849441
差分约束系统
一、概念
二、引例
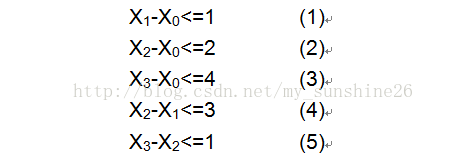
三、差分约束与最短路模型
1、与最短路模型的联系
先给出结论:求解差分约束系统,都可以转化成图论的单源最短路径(或最长路径)问题。
我们观察上面例子中的不等式,都是x[i] - x[j] <= a[k],可以进行移项,成为x[i] <= x[j] + a[k],我们令a[k] = w(j, i),dis[i]=x[i],并使i=v,j=u,那么原始就变为:dis[u]+w(u,v)>=dis[v],于是可以联想到最短路模型中的一部分代码
- if(dis[u]+w(u,v)<=dis[v])
- {
- dis[v]=dis[u]+w(u,v);
- }
这不正与松弛操作相似吗?
但是好像不等号方向刚好相反,但其实这并不矛盾
上面的代码要实现的是使dis[u]+w(u,v)>dis[v],而对于不等式,我们进行建边的操作:对于每个不等式 x[i] - x[j] <= a[k],对结点 j 和 i 建立一条 j -> i的有向边,边权为a[k],求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路,两者刚好吻合。所以求解差分约束问题就转化为了最短路问题。
2.问题解的存在性
由于在求解最短路时会出现存在负环或者终点根本不可达的情况,在求解差分约束问题时同样存在
(1)、存在负环
如果路径中出现负环,就表示最短路可以无限小,即不存在最短路,那么在不等式上的表现即X[n-1] - X[0] <= T中的T无限小,得出的结论就是 X[n-1] - X[0]的最大值不存在。在SPFA实现过程中体现为某一点的入队次数大于节点数。(貌似可以用sqrt(num_node)来代替减少运行时间)
(2)、终点不可达
这种情况表明X[n-1]和X[0]之间没有约束关系,X[n-1] - X[0]的最大值无限大,即X[n-1]和X[0]的取值有无限多种。在代码实现过程中体现为dis[n-1]=INF。
3、不等式组的转化
做题时可能会遇到不等式中的符号不相同的情况,但我们可以对它们进行适当的转化
(1)方程给出:X[n-1]-X[0]>=T ,可以进行移项转化为: X[0]-X[n-1]<=-T。
(2)方程给出:X[n-1]-X[0]<T, 可以转化为X[n-1]-X[0]<=T-1。
(3)方程给出:X[n-1]-X[0]=T,可以转化为X[n-1]-X[0]<=T&&X[n-1]-X[0]>=T,再利用(1)进行转化即可
4、应用
对于不同的题目,给出的条件都不一样,我们首先需要关注问题是什么,如果需要求的是两个变量差的最大值,那么需要将所有不等式转变成"<="的形式,建图后求最短路;相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成">=",建图后求最长路。
-----------------------------------------------------------------
本题就是差分约束的模板题,使用SPFA进行求解,在求解的过程中应该注意以下几个问题:
1.这道题用stack做,如果用queue会超时,在实现上除了把queue改成stack和front改为top别的没多大区别,更要注意栈的顺序是后进先出(LIFO),队列的顺序是先进先出(FIFO)。所以pop的位置要放对了。谁知道题里的数据用哪个不会超时呢(无奈)
2.邻接链表的实现。
SPFA全名是Shortest Path Faster Algorithmu也就是队列优化后的Bellman-Ford也是求单源最短路,他大概是这么来的:
n个顶点m条边。
第一个阶段:
对m条边最多遍历n-1次,也就是最多n-1次能把图中能松弛的都松弛完,这样找到最短路。(拿m条边一遍一遍的试,看能不能松弛一些距离)
第二个阶段:
在遍历的过程中可以发现,很多时候遍历不到n-1次就能松弛完,这时我们定义一个变量check对每轮松弛进行检测,如果到该轮松弛check没有发生变化说明整个图都已经松弛完毕,结束循环。(试到什么改变都不会发生了就说明松弛完了松弛不动了(⊙﹏⊙))
第三个阶段:
队列优化。在每实施一次松弛操作后,就会有一些顶点已经求得其最短路,此后这些顶点的最短路的估计值就会一直保持不变,不再受后续松弛操作的影响,但是每次还要判断是否需要松弛,这里浪费了时间。这就启发我们:每次仅对最短路估计值发生变化了的顶点的所有出边进行松弛操作。(联想到dijkstra在松弛过程中,松弛只对能松弛到的点产生影响,所以本轮松弛没有产生影响的点也不管他也就是不入队列,废话嘛不是)
即每次仅对最短路程发生变化了的点的相邻边执行松弛操作。
在存储图的时候我们选择邻接链表,方便使用queue或stack时寻找同一顶点发出的边。
邻接链表我也不是太熟悉
啊哈算法上有讲,最重要的是了解了邻接链表的模型:http://www.cnblogs.com/ahalei/p/3651334.html
如1先入队列,通过松弛,影响了1到2与4顶点的dis,然后把2,4入队列,1出队列。······直到队列为空。
这里的队列用queue和stack的区别只是pop的判断顺序不同,两个都要会吧Orz
咋那么多废话,快上代码
queue代码(超时):
#include<stdio.h>
#include<string.h>
#include<stack>
#include<queue>
#define INF 0x3f3f3f3f
using namespace std;
#define maxn 200000
struct node
{
int u,v,w,next;
} e[maxn];
int head[maxn],dis[maxn],book[maxn],n;
void spfa()
{
dis[1]=0;
book[1]=1;
queue<int> s;
s.push(1);
while(!s.empty())
{
int u=s.front();
s.pop();
for(int i=head[u];i!=-1;i=e[i].next)
{
if(dis[e[i].v]>dis[u]+e[i].w)
{
dis[e[i].v]=dis[u]+e[i].w;
if(book[e[i].v]==0)
{
book[e[i].v]=1;
s.push(e[i].v);
}
}
}
book[u]=0;
//s.pop();//队列可以写在这里(FIFO),但是为了以后方便统一的写法,还是都写在上面吧
}
}
int main()
{
int m;
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;i++)
{
dis[i]=INF;
}
memset(head,-1,sizeof(head));
memset(book,0,sizeof(book));
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
e[i].next=head[e[i].u];
head[e[i].u]=i;
}
spfa();
printf("%d\n",dis[n]);
}
return 0;
}
stack AC代码:
#include<stdio.h>
#include<string.h>
#include<stack>
#define INF 0x3f3f3f3f
using namespace std;
#define maxn 200000
struct node
{
int u,v,w,next;
} e[maxn];
int head[maxn],dis[maxn],book[maxn],n;
void spfa()
{
dis[1]=0;
book[1]=1;
stack<int> s;
s.push(1);
while(!s.empty())
{
int u=s.top();
s.pop();
for(int i=head[u];i!=-1;i=e[i].next)
{
if(dis[e[i].v]>dis[u]+e[i].w)
{
dis[e[i].v]=dis[u]+e[i].w;
if(book[e[i].v]==0)
{
book[e[i].v]=1;
s.push(e[i].v);
}
}
}
book[u]=0;
//s.pop();//不能写在这里,注意stack是LIFO!
}
}
int main()
{
int m;
while(~scanf("%d%d",&n,&m))
{
for(int i=1;i<=n;i++)
{
dis[i]=INF;
}
memset(head,-1,sizeof(head));
memset(book,0,sizeof(book));
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
e[i].next=head[e[i].u];
head[e[i].u]=i;
}
spfa();
printf("%d\n",dis[n]);
}
return 0;
}

