机器学习技法------SVM

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/a940902940902/article/details/84781041

Large Margain Separating Hyperplane

该节课的重点就是推导出 hard margin 的Linear SVM

对于线性分类器而言 例如感知机模型 如果测试数据和训练数据分布完全一致 那么上述三个分类器对于分类结果不会产生区别 但是在实际使用的过程中难免会有误差的存在 因此对于误差的容忍度也是度量一个分类器的重要标准
对于上述不同的分类器 对于数据的容忍度是不同的 所谓容忍度 是指分类器距离最近的样本之间的距离
换个角度 如果要找一个分类器到所有的分类样本之间的距离都很大 则该分类器和所有样本之间的Margin都很大,即这条线是很‘胖’的

接下来要做的是将上述语言转化为公式表达
max_w fat(f(w))
fat(f(w))= min_{n=1,2,3,4…n}distance(x_n,f(w))
上述式子只是增加了一个限制 首先要保证的是正确性 即:
Y=sign(Xw)

转化之后

假定我们已经拥有这样一个平面
w^Tx+b=0 求 distance（x,w,b）

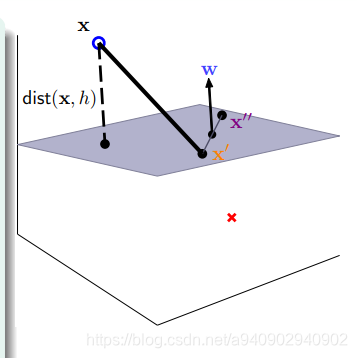
假设x^’和x^’’ j均为平面上的点 那么
w^Tx^’=-b 同理 w^Tx^‘’=-b
所以w^T(x^’-x^’’)=0 说明w垂直于平面上任意直线 即 w为平面的法向量
而点到平面的距离为 (x-x^’) 投影到垂直于平面的方向 即w的方向

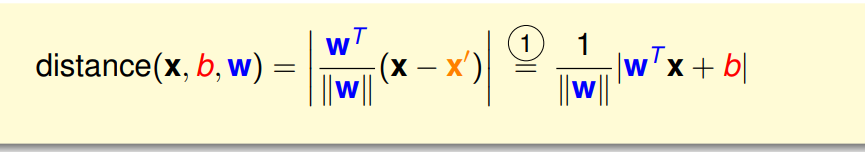
又因为 分割面能够正确分类 所以 y（w^Tx+b）>0
因此可以将距离公式进一步转化

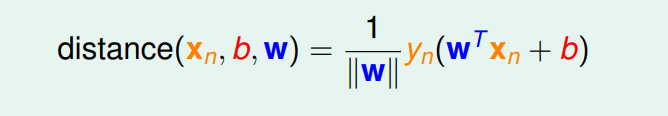
即

因为对于所有的x_n 样本为正的时候 w^Tx+b>0 样本为负的时候 w^Tx+b<0
此时如果我们同时缩放 w和b 那么就可以得到 w^Tx+b 大于任意一个数 此时为了方便计算我们取
w^Tx+b >=1 也就是说在margin边界上的数据可以取到1 那么此时

对于所有的x min 取到最小值即为x是边界上的点 这时 最小值为 1/w
所以目标函数变成 max _b,w 1/||w|| 同时w^Tx+b>=1 所以y_n(w^Tx+b)>0自然就会成立

进一步简化constraint
因为

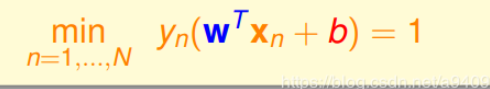
中存在一个min 使得该限制不好求解 可以转化一下思路 放宽一点限制 即对于所有的x_n都存在

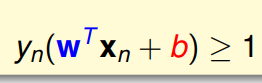
这个时候其实相当于放宽了条件限制 即 有可能出现所有的xn都大于1的情况 使得不存在等于1的那个边界 可是真的会存在这样的情况么 举个例子
如果存在这种情况

缩放之后依旧满足大于等于1的限制 但是max 1/||w|| 却变大了 所以不可能出现

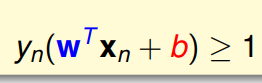
所有的结果都大于1并且在都大于1的情况下取到 1/||w|| 的最大值的
因此 这时新的问题变成

最后将最佳化问题转化为最小化代价函数

求解：
QP二次规划求解
因为最小化的式子对于w和b而言是有限制的 所以并不能很好的使用梯度下降的方法求解
这里要求解的式子是w的二次函数 而限制是w和b的线性组合
Hard-margin 不可以有分不开的情况

这里需要回去复习一下VC dimension
SVM相比于PLA并不是所有的分割都有效 是在分割基础之上增加了限制
这样导致了更少的dichotomy 根据VC dimension可知 Dichotomy越小 VC dimension越小 Ein和Eout接近的可能性越大
对于某个演算法的VC dimension 就是其最多能够shatter多少个点

这也就是说 SVM背后的基本保障：
减小了有效的VC dimension
可以控制复杂度 可控的复杂度导致Eout 会接近Ein

下一讲会将线性的分类 转化为非线性