关于float浮点数计算精度问题的深入分析

在Java中，或者说在任何一门语言中，float和double两种类型浮点数计算的精度问题都是老生常谈了。在进行跟钱相关的计算时(毕竟是白花花的银子)的时候如果不注意这两种浮点类型往往会出现许多莫名其妙的bug且难以排查，所以我们不管见到什么一股脑全用BigDecimal算了，也是一种你好我好大家好的万金油方案。但是为什么会有浮点数误差？Java中float有效位数为7位为什么却连0.1都存不了？为什么无所不能的计算机却连1-0.9=0.1这种小学生都会的计算都算不对？最近抽时间完整复习了一下组成原理中关于浮点数的章节，算是比较全面的解决了上述所有的疑问。现记下来备忘。如果各位观众有更好的理解欢迎指教。

万年不变的错误

在正式开始之前先看个例子，老生常谈了。

public static void main(String... args) {
    float a = 1;
    float b = 0.9f;
    System.out.println(a - b);
}

答案会是多少？
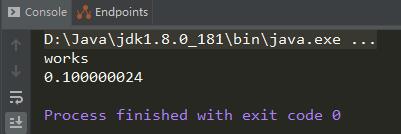
在这里插入图片描述
毫无疑问不是0.1，计算的结果是0.100000024。接下来我们由原理到现象来回答为什么是这个结果。

十进制与二进制

为什么要先说这个？CPU只认识0与1，我们输入的所有内容最终都将转换成二进制进行计算，而十进制与二进制转换的过程也就是浮点数误差出现的根本原因。
先复习一下大学课程计算机组成原理，十进制与二进制互转。

十进制整数

十进制转二进制采用”除二取余，倒序排列“的方式计算。整数依次除二直到商为0或1的时候结束，然后将所有余数倒序写出，不足位数的进行高位补0，结果即为对应的二进制。
一图胜千言

十进制小数

十进制小数的转换方式与整数恰巧相反，采用“乘二取整，顺序排列”的方法。将十进制小数部分取出进行乘二计算，将每一次计算得到的整数位取出排列，直至小数部分为0为止，不足位数的进行低位补0。下图以计算0.125为例。
在这里插入图片描述
到这里问题就出现了，进行除二操作的时候结果为0或1就可以结束，但是乘二操作要直到小数位为0为止。然而有些奇数进行乘二计算时永远也不会出现积为0的情况。比如0.9，按照上述规则进行计算得到的结果是这样的：

0.11100110011001100110011001100110011001100110011001100

最终结果将是1100无限循环下去。问题来了，计算机中存储是定长的，没有那么多空间来保存这个无限循环的东西，所以会砍掉一定的位数然后进行四舍五入得到近似值。假如我把上述二进制结果保留20位小数，然后重新转为十进制会得到什么结果？
误差从这里开始
结果离0.9有些差距了，而且随着保存精度越低，误差会越大。这个误差会随着计算逐渐累积直到导致程序bug。
但是float不是7位有效吗？要回答这个问题，需要知道float的"7位"是怎么来的。

浮点数在计算机中的保存方式

首先，计算机不认识小数点，IEEE 754标准规定浮点数在计算机内存中是按照一个特定的方式来保存的(充分利用了每一bit)。见下图。
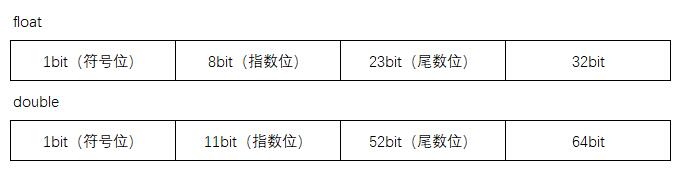
在这里插入图片描述
float在内存中共占32位，double共占64位，这也是单精度和双精度浮点数名称的由来。不过这和7位有效也没关系啊。
仔细观察这个结构，指数，尾数，是不是有点熟悉？没错，这就是浮点数以科学计数法在计算机内存中保存的样子。在IEEE 754标准中，严格的表示形式是这样的：
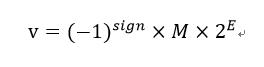
在这里插入图片描述
sign表示符号位，0为正，1为负。M表示尾数位，E表示指数位。对于float来说，指数位有8bit，也就是2⁸，所以float能表示数据的最大范围是-2¹²⁸~2¹²⁸。精度取决于尾数位，float有23bit的尾数位，但是由于尾数最高位总是为1所以将高位的1隐去，float尾数位实际上有24bit，2²⁴ = 16777216，这是一个最高8位的十进制数字，所以float有效位数为7位(对大部分编译器而言)，考虑到第七位可能存在舍入的情况，精确位数为6位。
现在回来看0.100000024这个结果，如果其值用float保存，取7位有效数字，是不是就变成0.1了？
需要特别注意的一点，float精度7位指的是整数位+小数位，而不仅仅是7位小数，当最高位为1时有8位精度？？？？？double在任何情况下都是16位精度
关于最高位隐去，现摘抄《深入理解计算机系统》一书原文以帮助理解。

小数字段flac被解释为描述小数值f，其中0 ≤ f＜1，其二进制表示为0. $f_{n-1}$ … $f_1$ $f_0$ ，也就是二进制小数点在最高有效位的左边。尾数定义为M = 1 + f。有时，这种方式也叫做隐含的以1开头的表示，因为我们可以把M看成一个二进制表达式1. $f_{n-1}$ … $f_1$ $f_0$ 的数字。既然我们总能够调整指数E，使得尾数M在范围1 ≤ M ＜2中(假设没有溢出)，那么这种表示方法是一种轻松获得一个额外精度位的技巧。既然第一位总是等于1，那么我们就不需要显式地表示它。

举个栗子

看以下代码

public static void main(String... args) {
    double b = 0.1f;
    System.out.println(b);
}

运行结果是什么？低精度转高精度，当然是0.1啊！然而现实并不是这样。
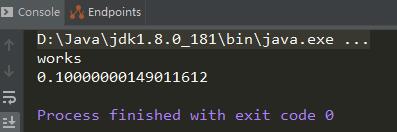
在这里插入图片描述
都说高精度转低精度会出现损失，但是为什么这里低精度转高精度却也出现了损失？是书上写错了吗？当然不是，下面我们运用上文的知识完整的推演一下整个进制转换的过程。
首先十进制0.1不能用二进制完全表示，其二进制形式为0.0001100[1100]…最后1100无限循环下去。
但是float精度不如double，float有23bit尾数，也就是在内存中保存的完整二进制应该是这样的

0.000110011001100110011001100

但是注意，尾数的第24位是1，会产生自动进位，也就是说，内存中实际保存的是这样的

0.000110011001100110011001101

重新进行十进制转换，得到结果。
在这里插入图片描述
其实这并不叫产生了误差，相反，由于低精度向高精度转换使得精度提高了，数字变得更精确了，用float保存的0.1f结果虽然会正确显示为0.1，但其实是精度截取再加上有效位数共同作用的结果，仅仅是一个巧合而已。

内容写的比较杂乱，很多地方是想到哪里写到哪里。如有遗漏或错误欢迎各位补充。