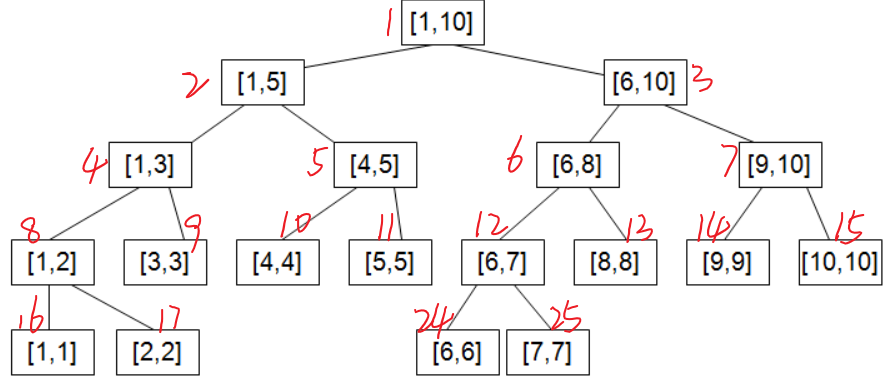
由图可得,叶子节点所存储的区间左右端点相等,为存储的最小单位;
观察每个节点的编号,可以发现并没有编号18-23的节点,因为同一父节点的两个子节点的编号完全取决于其父节点编号,而不是按照顺序编号,所以并不是所有数字都会用到。
首先需要定义一个结构体,其中元素包括区间左右端点,以及题目要求的需要进行区间维护的变量,以下以区间和为例。
定义结构体如下
struct segment_tree
{
int l,r;//区间左右端点
int val,lazy;//val为区间和,lazy为懒标记,后面再做解释
}t[MAXN*4];
每个节点存储的为该节点代表的区间内所有点的和,而每个父节点都被分成了两个没有交集的区间,因此很容易得出父节点的区间和应该为其两个子节点的区间和之和,每个叶子节点的区间和即为该点的值,所以我们可以从叶子节点从下到上依次推出每个父节点的值;
还是以[1,10]为例,设a1-a10的数值分别为1-10,即叶子节点的值为1-10,可画出权值图:

求初始的各节点区间和这一步是在建树时完成的,建树用递归来实现,具体代码如下:
1 void build(int p,int ll,int rr)//p为节点编号,ll,rr分别为区间左右端点
2 {
3 t[p].l=ll;
4 t[p].r=rr;
5 if(ll==rr)
6 {
7 t[p].val=a[ll];//如果为叶子节点,则区间和等于该点的值
8 return;
9 }
10 int mid=(ll+rr)>>1;
11 build(p<<1,ll,mid);//建立左子树
12 build(p<<1|1,mid+1,rr);//建立右子树
13 t[p].val=t[p<<1].val+t[p<<1|1].val;//维护区间和
14 }
上述代码中“(ll+rr)>>1”也可写成“(ll+rr)/2”,“p<<1”也可写成“p*2”,“p<<1|1”也可写成“p*2+1”
调用方式为build(1,1,n),表示根节点的区间左端点为1,右端点为n,再通过递归依次建立左子树和右子树,建立完成后不要忘记维护区间和,即该节点的值等于左右子节点之和
修改:
建树完成后我们就要进行区间修改,如果用传统暴力方法对区间内每个点都进行修改操作很容易超时,而线段树就很好地节省了时间(ps:在求区间和这类简单问题上,线段树较树状数组的优势并不明显,树状数组代码更为简洁,不过线段树用途更为广泛,可以解决许多复杂的问题,可根据题意选择用哪种算法)
还是以[1,10]为例,如果要将区间[3,7]内每个数都加3,过程如下:
1.从上往下遍历,如果该点所代表的区间包含在[3,7]内,则修改它的区间和,其子节点不需要再遍历,如下图,寻找到[3,3],[4,5],[6,7]包含在[3,7]内,[3,3]是叶子节点,所以只需要加3,[4,5],[6,7]都包含两个元素,所以需要加6,其子节点的值并没有修改,那么如果我们要查询4,5,6,7的值时,怎么判断其是否经过了修改呢?这就需要懒标记了,懒标记初始值为0,当我们修改[4,5],[6,7]这两个区间时,要将这两个节点的懒标记都加上3,代表这个区间内的每个点都加了3,当查询其子节点的值时,就要下放懒标记
其中下放懒标记的过程即为:将该节点的两个子节点的懒标记的值加上该节点的懒标记,并更新两子节点的区间和,将该节点的懒标记置零,代码如下:
1 void pushdown(int p)
2 {
3 t[p<<1].val+=(t[p<<1].r-t[p<<1].l+1)*t[p].lazy;
4 t[p<<1|1].val+=(t[p<<1|1].r-t[p<<1|1].l+1)*t[p].lazy;//更新左右子节点区间和
5 t[p<<1].lazy+=t[p].lazy;
6 t[p<<1|1].lazy+=t[p].lazy;//更新左右子节点懒标记,注意是“+=”
7 t[p].lazy=0;//父节点懒标记置零
8 }
注:
·懒标记可以重叠,所以在更新懒标记是一定记得是加,而不是直接等于,比如我们对某个区间进行两次修改操作,一次加2,一次加3,那么懒标记就变成了5,只需要在查询子区间时下放值为5的懒标记即可;
·懒标记是逐层下放,即一次只下放一层,而不是直接下放到叶子节点

2.在修改完这几个区间和之后,不要忘记维护父节点的值,如下图:

修改完得到的树为:

橙色是本次经过修改的点,可以看出线段树进行区间修改的复杂度为O(logn),比暴力的O(n)快了很多
代码实现如下:
1 void add(int p,int ll,int rr,int k)
2 {
3 if(t[p].l>=ll&&t[p].r<=rr)
4 {
5 t[p].val+=(t[p].r-t[p].l+1)*k;
6 t[p].lazy+=k;
7 return;
8 }//如果该区间包含在需修改区间内,则修改其权值,懒标记设为k
9 if(t[p].lazy)
10 pushdown(p);//下放懒标记
11 int mid=(t[p].l+t[p].r)>>1;
12 if(ll<=mid)
13 add(p<<1,ll,rr,k);//修改左子树
14 if(rr>mid)
15 add(p<<1|1,ll,rr,k);//修改右子树
16 t[p].val=t[p<<1].val+t[p<<1|1].val;//维护区间和
17 }
查询:
对于上述修改后的线段树进行区间查询,以查询区间[5,10]为例,与修改类似,从上往下遍历,如果该区间包含于查询区间内,则加上该区间的区间和即可,对于此查询,我们只需要加[5,5]和[6,10]的区间和,[6,10]区间和为46,直接加上即可,而[5,5]的值在上一步修改中并没有被修改,所以不能直接加上5,而要先下放其父节点的懒标记,将[5,5]的值更新为8,然后才能进行加和
查询具体代码如下:
1 int query(int p,int ll,int rr)
2 {
3 if(t[p].l>=ll&&t[p].r<=rr)
4 return t[p].val;//如果该区间包含在查询区间内,则直接返回该区间和
5 int ans=0;
6 if(t[p].lazy)
7 pushdown(p);//下放懒标记
8 int mid=(t[p].l+t[p].r)>>1;
9 if(ll<=mid)
10 ans+=query(p<<1,ll,rr);//查询左子树
11 if(rr>mid)
12 ans+=query(p<<1|1,ll,rr);//查询右子树
13 return ans;
14 }
AC代码如下:

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define MAXN 100005 4 struct segment_tree 5 { 6 int l,r; 7 long long val,lazy; 8 }t[MAXN*4]; 9 int a[MAXN]; 10 void build(int p,int ll,int rr) 11 { 12 t[p].l=ll; 13 t[p].r=rr; 14 if(ll==rr) 15 { 16 t[p].val=a[ll]; 17 return; 18 } 19 int mid=(ll+rr)>>1; 20 build(p<<1,ll,mid); 21 build(p<<1|1,mid+1,rr); 22 t[p].val=t[p<<1].val+t[p<<1|1].val; 23 } 24 void pushdown(int p) 25 { 26 t[p<<1].val+=(t[p<<1].r-t[p<<1].l+1)*t[p].lazy; 27 t[p<<1|1].val+=(t[p<<1|1].r-t[p<<1|1].l+1)*t[p].lazy; 28 t[p<<1].lazy+=t[p].lazy; 29 t[p<<1|1].lazy+=t[p].lazy; 30 t[p].lazy=0; 31 } 32 void add(int p,int ll,int rr,int k) 33 { 34 if(t[p].l>=ll&&t[p].r<=rr) 35 { 36 t[p].val+=(t[p].r-t[p].l+1)*(long long)k; 37 t[p].lazy+=k; 38 return; 39 } 40 if(t[p].lazy) 41 pushdown(p); 42 int mid=(t[p].l+t[p].r)>>1; 43 if(ll<=mid) 44 add(p<<1,ll,rr,k); 45 if(rr>mid) 46 add(p<<1|1,ll,rr,k); 47 t[p].val=t[p<<1].val+t[p<<1|1].val; 48 } 49 long long query(int p,int ll,int rr) 50 { 51 if(t[p].l>=ll&&t[p].r<=rr) 52 return t[p].val; 53 long long ans=0; 54 if(t[p].lazy) 55 pushdown(p);//下放懒标记 56 int mid=(t[p].l+t[p].r)>>1; 57 if(ll<=mid) 58 ans+=query(p<<1,ll,rr); 59 if(rr>mid) 60 ans+=query(p<<1|1,ll,rr); 61 return ans; 62 } 63 int main() 64 { 65 int n,m,x,y,k,i,flag; 66 long long sum; 67 cin>>n>>m; 68 for(i=1;i<=n;i++) 69 scanf("%d",&a[i]); 70 build(1,1,n); 71 while(m--) 72 { 73 scanf("%d",&flag); 74 if(flag==1) 75 { 76 scanf("%d%d%d",&x,&y,&k); 77 add(1,x,y,k); 78 } 79 else 80 { 81 scanf("%d%d",&x,&y); 82 sum=query(1,x,y); 83 cout<<sum<<endl; 84 } 85 } 86 return 0; 87 }
Author:hiang Date:2019.5.26
