本文来自网易公开课的<算法导论>第3讲分治法。让我对分治法的使用有了一个新的认识斐波那契数列，又称黄金分割数列，F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2，n∈N*）
下面我将使用Java(是的，又是Java，不过我觉得没什么问题，算法嘛，重在思想)来分别实现这三种方法。后来视频看到一半，发现使用朴素递归方法求解该问题时，有许多重复的子问题，那么这就符合动态规划的基本思想了，可以将采用自底向上的求解顺序，保存子问题的结果。这样做的算法时间是：theta(n)
1.朴素递归：自定向向下求解问题，导致了大量的重复求解
2.动态规划：准确的讲应该是一种自底向上的"动态规划"思想解法。
3.数学归纳法(线性代数矩阵连乘公式)
设Fn表示第n个斐波那契数，那么有定理:
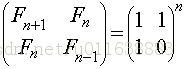
证明：当n=1,F0=0,F1=1,F2=2，即：
那么假设定理成立，将n-1带入可得表达式：
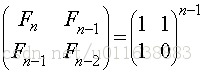
即：
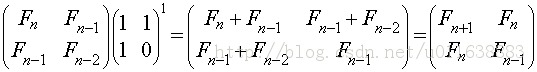
因为等式
恒成立，于是假设成立。
这样就将斐波那契数列转换成了n乘方问题了，那么n乘方问题的算法时间为什么不是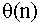
，而是
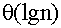呢？这里可以使用分治法求解n乘方问题，可将n个数连乘分成左右相等的两部分(偶数d的话n/2和n/2,奇数的话(n-1)/2和(n-1)/2)。就有：
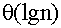这样n个数连乘，只需划分次即可。
代码如下:
package com.wly.algorithmproblem;
/**
* 解斐波拉契数列问题，使用三种方法：朴素递归解法、自底向上的动态规划思想解法、线性代数矩阵连乘公式解法
* @author wly
* @date 2013-11-28
*
*/
public class FibonacciSequence {
private static int TESTCASE = 43;
private static int[][] matrixUnit = {{1,1},{1,0}};
public static void main(String[] args) {
System.out.println("测试规模:" + TESTCASE);
//---朴素递归解斐波那契数列问题测试
long startT = System.currentTimeMillis();
System.out.println("朴素递归:" + simpleRecurrence(TESTCASE));
System.out.println("朴素递归用时:" + (System.currentTimeMillis()-startT));
//---自底向上(动态规划)解斐波那契数列问题测试
startT = System.currentTimeMillis();
System.out.println("自底向上(动态规划):" + downToTopReslove(TESTCASE));
System.out.println("自底向上(动态规划)用时:" + (System.currentTimeMillis()-startT));
//---线性代数矩阵解斐波那契数列问题测试
int[][] mResult = {{1,1},{1,0}};
startT = System.currentTimeMillis();
int n = 1;
while(n<TESTCASE) {
mResult = matrixMutiple(mResult, matrixUnit);
n ++;
}
System.out.println("线性代数矩阵公式:" + mResult[0][1]);
System.out.println("线性代数矩阵公式用时:" + (System.currentTimeMillis()-startT));
//分治法求m的n连乘测试
System.out.println("分治法求2的23连乘:" + pow(2, 23));
//两矩阵相乘方法测试
/*
int[][] matrix1 = {{2,3,4},{1,2,3}};
int[][] matrix2 = {{2,4},{3,5},{4,6}};
int[][] result = new int[matrix1.length][matrix2[0].length];
int[][] resultS = matrixMutiple(matrix1,matrix2,result);
System.out.println();
*/
}
/**
* 朴素递归
* @param n
* @return 第n个斐波那契数
*/
public static int simpleRecurrence(int n) {
if(n == 0) {
return 0;
}
if(n == 1 || n == 2) {
return 1;
}
return simpleRecurrence(n-1) + simpleRecurrence(n-2);
}
/**
* 自底向上包含"动态规划"思想的解法
* @param n
* @return 第n个斐波那契数
*/
public static int downToTopReslove(int n) {
if(n == 0) {
return 0;
} else if(n == 1 || n == 2) {
return 1;
} else {
int[] fibonacciArray = new int[n+1]; //fibonacciArray[i]表示第i个斐波那契数
fibonacciArray[0] = 0;
fibonacciArray[1] = 1;
fibonacciArray[2] = 1;
for(int i=3;i<=n;i++) { //注意由于fibonacciArray[0]表示第0个元素，这里是i<=n，而不是i<n
fibonacciArray[i] = fibonacciArray[i-1] + fibonacciArray[i-2];
}
return fibonacciArray[fibonacciArray.length-1];
}
}
/**
* 分治法求解factor的n次方
* @param factor 基数
* @param n 次方数
* @return
*/
public static long pow(long factor,int n) {
if(n == 0) {
return 1;
} else if(n == 1){
return factor;
} else {
if(n % 2 == 1) { //乘法数为奇数
return pow(factor,(n-1)/2) * pow(factor, (n-1)/2) * factor;
} else { //乘方数为偶数
return pow(factor, n/2) * pow(factor, n/2);
}
}
}
/**
* 两矩阵相乘
* @param matrix1
* @param matrix2
* @return
*/
public static int[][] matrixMutiple(int[][] matrix1,int[][] matrix2) {
int[][] result = new int[matrix1.length][matrix2[0].length];
for(int i=0;i<matrix1.length;i++) {
for(int j=0;j<matrix2[i].length;j++) {
int temp = 0;
for(int k=0;k<matrix1[0].length;k++) {
temp = matrix1[i][k] * matrix2[k][j] + temp;
}
result[i][j] = temp;
}
}
return result;
}
}测试规模:43
朴素递归:433494437
朴素递归用时:1669
自底向上(动态规划):433494437
自底向上(动态规划)用时:0
线性代数矩阵公式:433494437
线性代数矩阵公式用时:1
分治法求2的23连乘:8388608 这里有一点需要说明的是，代码中已经包含了m的n次方的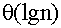代码。本来想讲它结合到第三种线性代数矩阵连乘的解法中的，但是后来发现那样的话，代码显得很乱，于是就只是简单的使用while来连乘了n次实现。总的来说还是实现了三种不同的解斐波拉契数列的方法，希望能够大家一点参考
O啦~~~
转载请保留出处:
谢谢!!
转载于:https://my.oschina.net/cjkall/blog/195815