并查集
概念:
在计算机科学中,并查集是一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。有一个联合-查找算法(union-find algorithm)定义了两个用于此数据结构的操作:
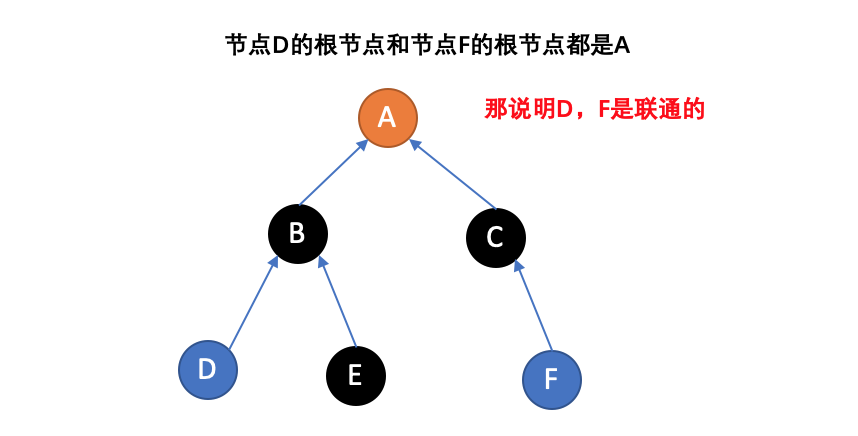
- Find:确定元素属于哪一个子集。这个确定方法就是不断向上查找找到它的根节点,它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合
由于支持这两种操作,一个不相交集也常被称为联合-查找数据结构(union-find data structure)或合并-查找集合(merge-find set)。其他的重要方法,MakeSet,用于建立单元素集合。有了这些方法,许多经典的划分问题可以被解决。
为了更加精确的定义这些方法,需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素,称为代表,以表示整个集合。接着,Find(x) 返回 x 所属集合的代表,而 Union 使用两个集合的代表作为参数。

并查集森林
并查集森林是一种将每一个集合以树表示的数据结构,如上图所示。其中每一个节点保存着到它的父节点的引用(见意大利面条堆栈)。这个数据结构最早由Bernard A. Galler和Michael J. Fischer于1964年提出,[1]但是经过了数年才完成了精确的分析。
在并查集森林中,每个集合的代表即是集合的根节点。“查找”根据其父节点的引用向根行进直到到底树根。“联合”将两棵树合并到一起,这通过将一棵树的根连接到另一棵树的根。实现这样操作的一种方法是
function MakeSet(x) x.parent := x function Find(x) if x.parent == x return x else return Find(x.parent) function Union(x, y) xRoot := Find(x) yRoot := Find(y) xRoot.parent := yRoot
这是并查集森林的最基础的表示方法,这个方法不会比链表法好,这是因为创建的树可能会严重不平衡;然而,可以用两种办法优化。
优化方法一:按秩合并
第一种方法,称为“按秩合并”,即总是将更小的树连接至更大的树上。因为影响运行时间的是树的深度,更小的树添加到更深的树的根上将不会增加秩除非它们的秩相同。在这个算法中,术语“秩”替代了“深度”,因为同时应用了路径压缩时(见下文)秩将不会与高度相同。单元素的树的秩定义为0,当两棵秩同为r的树联合时,它们的秩r+1。只使用这个方法将使最坏的运行时间提高至每个MakeSet、Union或Find操作、0(\logn)。
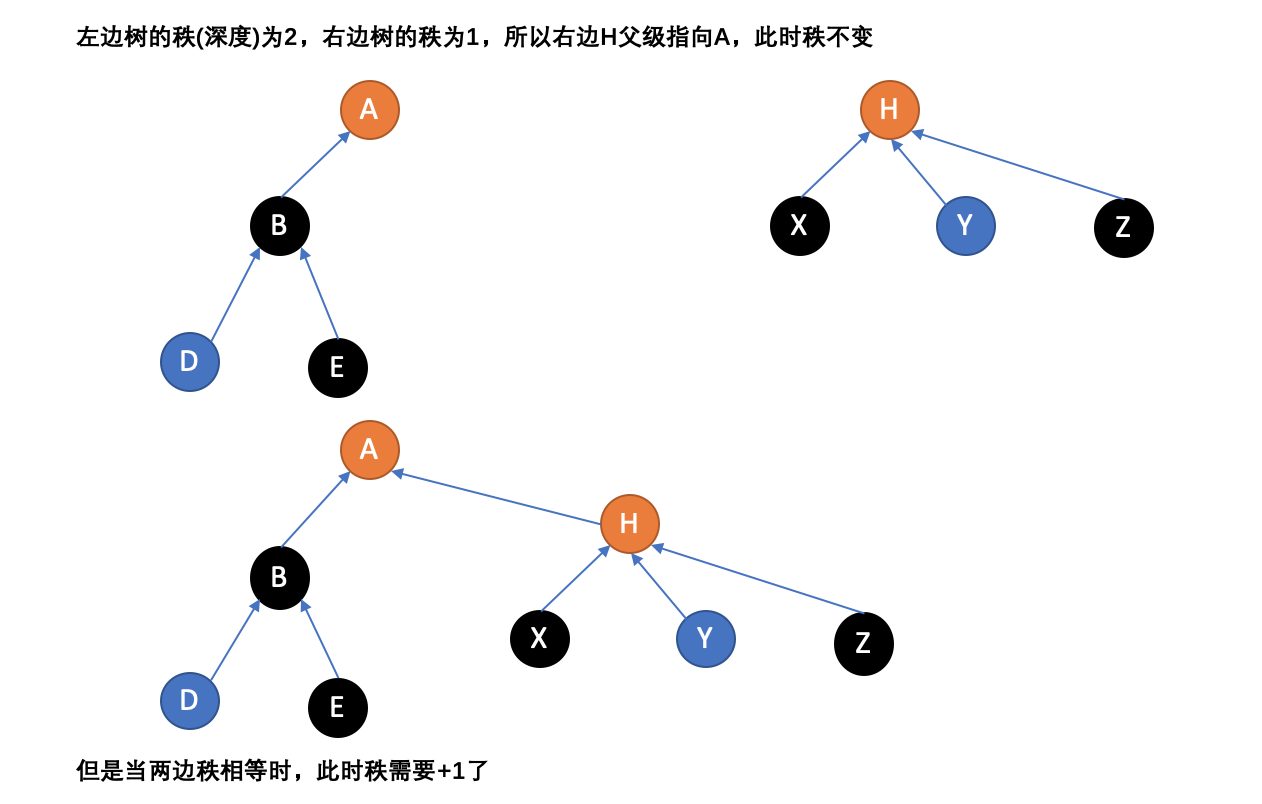
优化后的MakeSet和Union伪代码:
function MakeSet(x) x.parent := x x.rank := 0 function Union(x, y) xRoot := Find(x) yRoot := Find(y) if xRoot == yRoot return // x和y不在同一个集合,合并它们。 if xRoot.rank < yRoot.rank xRoot.parent := yRoot else if xRoot.rank > yRoot.rank yRoot.parent := xRoot else yRoot.parent := xRoot xRoot.rank := xRoot.rank + 1
优化方法二:路径压缩
第二个优化,称为“路径压缩”,是一种在执行“查找”时扁平化树结构的方法。关键在于在路径上的每个节点都可以直接连接到根上;他们都有同样的表示方法。为了达到这样的效果,Find递归地经过树,改变每一个节点的引用到根节点。得到的树将更加扁平,为以后直接或者间接引用节点的操作加速。
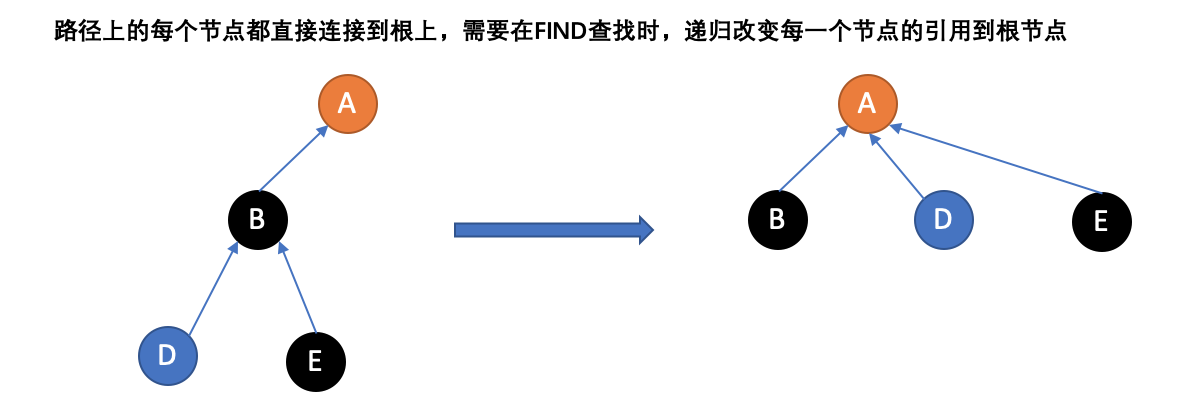
这儿是Find:
function Find(x) if x.parent != x x.parent := Find(x.parent) return x.parent
合并两个不相交集合
操作很简单:先设置一个数组(阵列)Father[x],表示x的“父亲”的编号。 那么,合并两个不相交集合的方法就是,找到其中一个集合最父亲的父亲(也就是最久远的祖先),将另外一个集合的最久远的祖先的父亲指向它。
void Union(int x,int y) { fx = getfather(x); fy = getfather(y); if(fy!=fx) father[fx]=fy; }
判断两个元素是否属于同一集合
仍然使用上面的数组。则本操作即可转换为寻找两个元素的最久远祖先是否相同。寻找祖先可以采用递归实现,见后面的路径压缩算法。
bool same(int x,int y) { return getfather(x)==getfather(y); } /*返回true 表示相同根结点,返回false不相同*/
641.并查集-臭虫也疯狂 (10分)
C时间限制:1000 毫秒 | C内存限制:3000 Kb
题目内容:
霍普教授研究臭虫的性取向。实验前他弄清楚了n个臭虫的性别,并在臭虫的背上标了数字编号(1~n)。现在给一批臭虫的编号
配对,要检查里面有没有同性恋。
输入描述
第一行是整数c,下面接着有c个测试用例。
每个测试用例的第一行是臭虫的数目n(1~2000),以及配对的数目m(1~10^6)。接下来的行就是m个配对的臭虫编号.
输出描述
一共c行, 每行打印“testcase i:没有发现同性恋”,或者“testcase i:发现同性恋”
输入样例
2
3 3
1 2
2 3
1 3
4 2
1 2
3 4
输出样例
testcase 1:发现同性恋
testcase 2:没有发现同性恋
思路:
代码1的思路:
这个代码是超时的,3s应该能过,但是1s就超时了,但是我还是想把这个代码放进去
整体思路:pre数组是存你的祖先的,enemy是存你的敌人的
因为性别是雌雄,所以相当于分成两堆臭虫
每输入一组x,y时,判断x,y他们的祖先是否是一样的,也就是说是否在一堆里面,如果在一堆,那么性别相同,所以发现同性恋
如果不相同,if(enemy[x]) join(enemy[x],y); 那么就把enemy[x]和y合在一堆,也就是说x和y是分别的两堆,那么性别一定不相同,enemy[x]也与x性别不相同,就是说enemy[x]与y的性别是相同的,所以合并成一堆,找到enemy[x]的祖先,然后就让enemy[x]的祖先指向y的祖先。
if(enemy[y])一样的理解
最后分别把各自的敌人记录下来。
代码1:
#include<iostream> #include<stdio.h> #include<string.h> using namespace std; const int maxn = 2001; int pre[maxn],enemy[maxn]; int find(int x){ return pre[x] == x?x:find(pre[x]); } void join(int x,int y){ pre[find(x)] = find(y); } bool judge(int x,int y){ return find(x)==find(y); } int main() { int t; cin>>t; for(int i=1;i<=t;i++){ int n,m; cin>>n>>m; for(int i=1;i<=n;i++) pre[i] = i; memset(enemy,0,sizeof(enemy));//不能掉 bool flag = true; for(int i=1;i<=m;i++){ int x,y; scanf("%d%d",&x,&y); if(judge(x,y)){ flag = false; } else{ if(enemy[x]){ join(enemy[x],y); } if(enemy[y]){ join(enemy[y],x); } enemy[x] = y; enemy[y] = x; } } printf("testcase %d:",i); if(!flag) cout<<"发现同性恋"<<endl; else cout<<"没有发现同性恋"<<endl; } return 0; }
思路:
这个代码是没有超时的,这个就很有趣了,当然理解了好久,勉勉强强的懂了
种类并查集:
首先f[i]存储的是自己的祖先,开始时,每个都是一个独立的集合,相当于说祖先就是自己
r[i]存储的是i与f[i]的关系,如果r[i]==0,就是i与f[i]是同性,当r[i]==1时,是异性
种类并查集和基础并查集大致一样,多了两句代码:getf函数中的 r[x] = (r[x] + r[f[x]]) % 2 和 Union函数中的 r[fb] = (r[a]+1-r[b]+2)%2,不用多想,这两句就是种类并查集的关键,所以在这里就重点解释这两句的意思。
getf函数中的 r[x] = (r[x] + r[f[x]]) % 2:
这一句其实是实时更新 r[x], 因为我们知道,在压缩路径的同时,x的直接父节点f[x]可能就会变了(变的话就是变为root),所以r[x]也可能随之改变,怎么变呢?是不是可以这样表示:root->x = root->f[x] + f[x]->x。有可能你会问,root也不一定是f[x]的直接父节点啊,记住,因为路径压缩是递归的,所以在此之前,root已经是f[x]的直接父节点了,所以root->f[x] 这一句是没毛病的。
Union函数中的 r[fb] = (r[a]+1-r[b]+2)%2:
在Union函数中涉及了两种情况:fa == fb,即a,b根节点相同,属于同一棵树,只判断a和b跟根节点的关系是否相同就行了,即r[a] == r[b]。
fa != fb时,分属两棵树,需要将它们联系在一起,做法就是将一个根节点挂在另一个根节点上,即f[fb] = fa,同时更新 r数组的关系,怎么更新?我们的做法是将fb挂在fa上,根据我们定义的关系,可以这样表示 fa->fb = fa->a + a->b + b->fb,翻译过来就是r[fb] = (r[a] + 1 - r[b] + 2) %2,其中 + 1是题目暂时给出的关系,为异性,+2是避免负数。
a->b 为1,因为刚开始输入的时候a和b就是异性的关系,所以为1。
代码2:
#include<iostream> #include<stdio.h> using namespace std; const int maxn = 2001; int f[maxn],r[maxn]; bool flag; int getf(int x){ if(x==f[x]) return x; int t = getf(f[x]); r[x] = (r[x]+r[f[x]])%2; f[x] = t; return t; } void Union(int a,int b){ int fa = getf(a); int fb = getf(b); if(fa==fb){ if(r[a]==r[b]) flag= false; return ; } f[fb] = fa;; r[fb] = (r[b]+1-r[a]+2)%2; } int main(){ int t; cin>>t; for(int i=1;i<=t;i++){ int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ f[i] = i; r[i] = 0; } flag =true; int a,b; for(int i=1;i<=m;i++){ scanf("%d%d",&a,&b); if(flag) Union(a,b); } printf("testcase %d:",i); if(!flag) cout<<"发现同性恋"<<endl; else cout<<"没有发现同性恋"<<endl; } return 0; }