图论（2） 最小生成树与最短路径问题

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/weixin_41611045/article/details/89454839

一、最小生成树
1、定义
假定G是一个图，其中的边是带有给定权值，自然也可以做出它的生成树，先将G中一棵树中各个边的权值之和称为该生成树的权。
图G可能存在多种不同的生成树，不同生成树的权值也可能不一样，其中权值最小的生成树称为G的最小生成树，显然任何一张图都有其最小生成树，但最小生成树可能不唯一。
总结：最小生成树可以总结为找v-1条边，连接v个顶点，总权值最小。
2、最小生成树的算法
2.1 krusal算法
这是一个构建最小生成树的简单算法：
设G=(V,E)是一个图，V有n个顶点，则利用krusal构建最小生成树的过程如下：
（1）初始时选取所有的n个顶点构成孤立点的子图T={}
（2）将边集E按权值递增的顺序排序，顺序的检查边序列，找到下一条两端点位于T的两个不同联通分量的边e，把e加入T.
（3）不断连接T的顶点数，直到找到n-1条边将其所有的顶点连接。这些联通分量形成的集合就是一个最小生成树。
例：



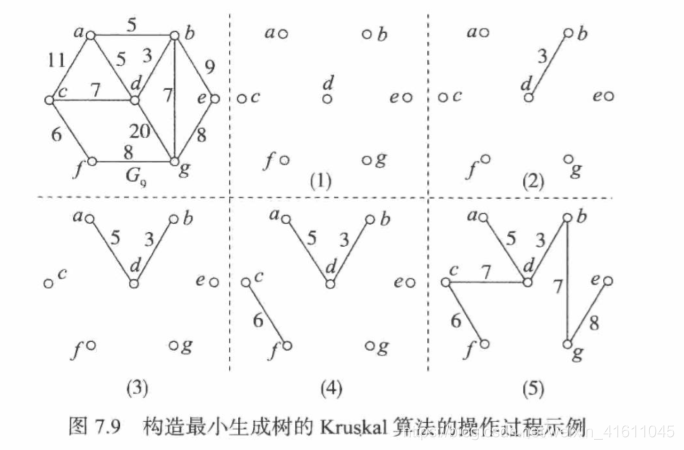
为了方便起见，我们将上面的例子改一下，变为：

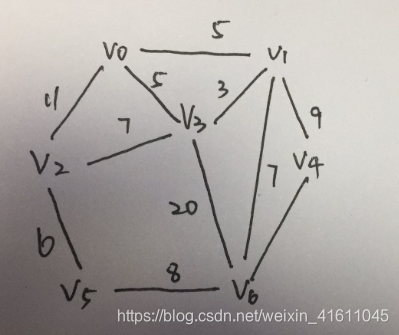
            图2
解析：我们在进行这个算法时有两个问题需要解决，
一是最短边的选择，我们可以采取排序的方式，将边的集合变为（w,i,j）,w代表各个边的权重，i、j代表这个边是从顶点i到顶点j的，然后将前面的集合进行排序，（python 默认对第一个集合的第一个元素排序）
二是：怎么确定这个点是否已经联通了，我们采用reps这个样一个联通元来实现，reps初始值为[1,2,3…n]由n个顶点组成的有序列表，其索引表示各个下标，如果2和3已经联通，则两者的索引变为同一数字，即[1,2,2,…]依次类推
代码实现：
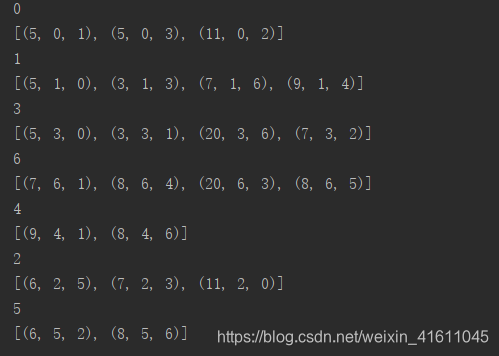
限于篇幅原因我们还是只邻接表的最小生成树，我们首先先为以后的边的集合做个准备，我们将之前sparsegraph()中的迭代器做个修改，其中iterator_edg表示顶点相邻边的集合

    class adjiiterator():
        def __init__(self,g,v):
            self.g=g
            self.v=v
            self.connect_ede=[]

        def iterator(self):
            if self.v in self.g.vertixlist.keys():
                print(self.v,"：",end="")
                for i in self.g.vertixlist[self.v].connect_to.keys():
                    print(i,end=" ")
            else:
                return -1
        def iterator_edg(self): #顶点的领边集合
            if self.v in self.g.vertixlist.keys():
                v=self.v
                for i in self.g.vertixlist[self.v].connect_to.keys():
                    w=self.g.vertixlist[self.v].connect_to[i]
                    self.connect_ede.append((w,v,i))
                return self.connect_ede
            else:
                return -1


#测试，以图2做测试
graph_1=sparsegraph(directed=False)
graph_1.addedge(0,1,5)
graph_1.addedge(0,3,5)
graph_1.addedge(3,1,3)
graph_1.addedge(1,6,7)
graph_1.addedge(1,4,9)
graph_1.addedge(4,6,8)
graph_1.addedge(3,6,20)
graph_1.addedge(2,5,6)
graph_1.addedge(2,3,7)
graph_1.addedge(2,0,11)
graph_1.addedge(5,6,8)
for i in graph_1.vertixlist:
    print(i)
    print(graph_1.adjiterator(graph_1,i).iterator_edg())

最小生成树代码的实现：

##krusakal 最小生成树
def kruskal(g):
    vnum=g.numvertix
    reps=[i for i in range(vnum)]
    #mst记录最小的生成树的边，edges记录所有的边
    mst,edges=[],[]
    for vi in range(vnum):
        for edg in g.adjitertor(g,vi).iterator_edg():
            edges.append(edg)
    edges.sort()
    print(edges)
    for w,vi,vj in edges:
        if reps[vi] != reps[vj]:
            mst.append((vi,vj,w))
            if len(mst)==vnum-1:
                break
            rep,orep=reps[vi],reps[vj]
            for i in range(vnum):#归并联通元
                if reps[i]==orep:
                    reps[i]=rep
    print(reps)
    return mst
###测试代码
print("#######################################最小生成树")
graph_1=sparsegraph(directed=False)
graph_1.addedge(0,1,5)
graph_1.addedge(0,3,5)
graph_1.addedge(3,1,3)
graph_1.addedge(1,6,7)
graph_1.addedge(1,4,9)
graph_1.addedge(4,6,8)
graph_1.addedge(3,6,20)
graph_1.addedge(2,5,6)
graph_1.addedge(2,3,7)
graph_1.addedge(2,0,11)
graph_1.addedge(5,6,8)
print(kruskal(graph_1))

结果：

（1）前一个为函数中reps联通元的结果，顶点0、1、2、3、5、6均为同一数字，代表这几个顶点已经联通，由于最后一个顶点自然联通，所以不用进行联通，所以顶点4没有执行联通操作。
（2）后面的集合即为最小生成树，分为为vi,vj,w,即边的集合，vi起点，vj终点，w权值。

例2：简单实现最小生成树
上面的实现是采用邻接矩阵进行实现的，下面我们采用简单的方法对其进行实现

'''
最小生成树1：kural算法
0：
0->1:5,0->3:5
1:
1->3:3,1->4:9,1->6:7
2:
2->0:11,2->3:7,2->5:6
3:
3->0:5,3->2:7,3->6:20
4:
4->1:9,4->6:7
5:
5->2:6,5->6:8
6:
6->1:7,6->3:20,6->4:7,6->5:8
'''
matrix=[[0,5,0,5,0,0,0],
        [0,0,0,3,9,0,7],
        [11,0,0,7,0,6,0],
        [5,0,7,0,0,0,20],
        [0,9,0,0,0,0,7],
        [0,0,6,0,0,0,8],
        [0,7,0,20,7,8,0]]
n=len(matrix[0])
#设置一个连通元，来记录顶点之间是否能相互连通，（a,b相互联通的意思是指，顶点a能通过边的传播到达顶点b）
rep=[i for i in range(n)]
edge=[]
for i in range(n):
    for j in range(n):
        if matrix[i][j]!=0:
            edge.append([i,j,matrix[i][j]])
edge.sort(key=lambda x:x[2],reverse=True)
arr=[] #arr记录最小生成树的集合
while edge:
    print(rep)
    print(arr)
    bian=edge.pop()
    start=bian[0]
    end=bian[1]
    w=bian[2]
    if len(edge)==n-1:
        break
    if rep[start]!=rep[end]:
        arr.append(bian)
        #归并联通元
        a,b=rep[start],rep[end]
        for i in range(n):
            if rep[i]==a:
                rep[i]=b
    else:
        continue
权重之和=sum([i[2] for i in arr])
print("最小生成树的权重是:"+str(权重之和))
    

生成的最小生成树：
[[1, 3, 3], [3, 0, 5], [5, 2, 6], [6, 4, 7], [6, 1, 7], [3, 2, 7]]
最小生成树的权重是:35
2.2 prim算法
1、切分定理
对于一个图来说，给定任意的切分，横切边中权值最小的边必然属于最小生成树

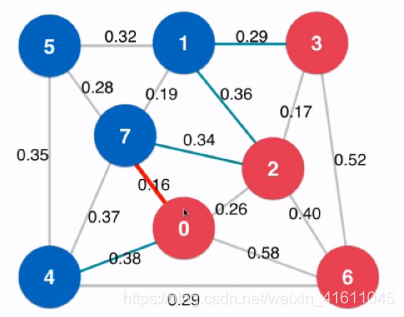
切分定理简单证明：
我们将一个图G分为两部分，设为G1和G2,则这两图中一定有横切边，因为这两个图必然是联通的，这时我们添加其横切边的任意一条边，便可以将两个最小生成树联通，其中横切边最小的边组成的便是最小的生成树，同时横切边中任意一条边加入这个生成树都会形成回路，所以这些横切边中有且仅有一条权值最小的边为图G的最小生成树的边
2、prim算法
prim算法是利用切分定理，来求最小生成树，其细节可以表示为：
（1）从图G的顶点集V中任取任一顶点放入集合U中，这时U={V0},边的集合为 $E_T=${},这时T=(U, $E_T$)显然是一个最小生成树（一个顶点没有边）
（2）检查所有一个端点在集合U另一个端点在集合V-U的边，找出其中权值最小的边e=(u,v),将顶点v加入集合u中，将e加入集合 $E_T$中。
（3）重复上面步骤直到U中所有的顶点都加入u中。

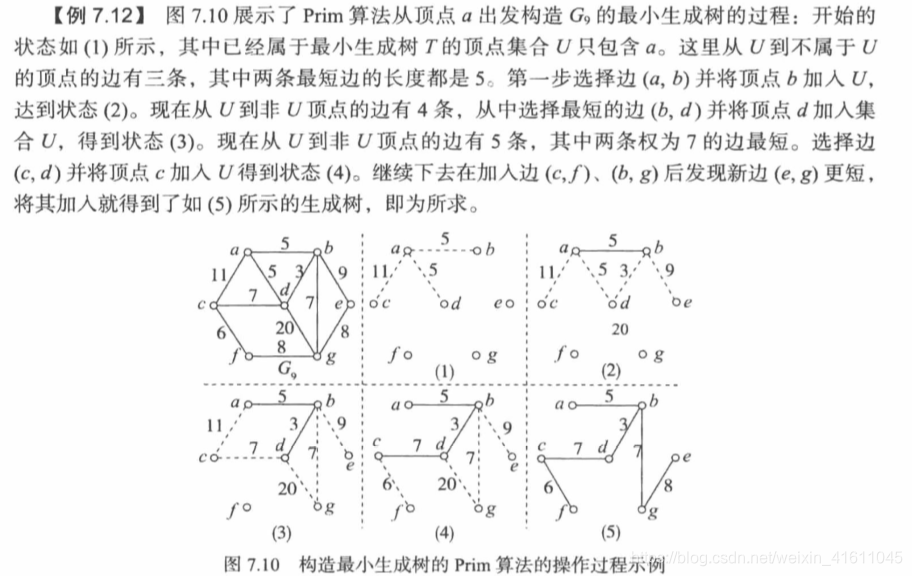
难点1：怎么确定其中的横切边呢，我们可以选择将联通的顶点的相邻边加入来确定接下来将要选择的最小权值，以上面的图为例，设横切边集合为E_n={},首先是a，与a相邻的有三个边E_n={ab,ad,ac},选取最短边ab，则集合变为{ad,ac},再将b的相邻边加入进来，则集合变为E_n={ad,ac,bd,bc},选取最短边bd，d的相邻边加入E_n,E_n={ad,ac,bc,dc,dg},如此反复，直到所有顶点都被遍历完。这里我们可以采用优先队列的方式去实现。
同样还是以上面图2进行最小生成树的测试
代码实现：

#优先队列的实现
class prioQueue:
    def __init__(self,elist=[],reverse=True):
        self.prio_list=list(elist)
        self.reverse=reverse
        self.prio_list.sort(reverse=self.reverse)
    def enqueue(self,e): #入队列
        i = len(self.prio_list) - 1
        #如果元素中小的为优先级
        if self.reverse==True:
            while i>=0:
                if self.prio_list[i][0]<=e[0]:
                    i-=1
                else:
                    break
            self.prio_list.insert(i+1,e)
        else: #最大的优先级
            while i>=0:
                if self.prio_list[i][0]>=e[0]:
                    i-=1
                else:
                    break
            self.prio_list.insert(i+1,e)
    def is_empty(self):
        if self.prio_list == []:
            return True
        else:
            return False
    def dequeue(self): #出队
        if self.is_empty():
            print("队列为空，无法出队")
            return
        else:
            return self.prio_list.pop()
#prim最小生成树的实现
def prim(g,v):
    #传入两个参数，一个图的名字，一个遍历开始顶点的名字
    vnum=g.numvertix
    """
    mst记录所有顶点被访问的记录，同时记录最小生成树的生成结果，其中的v代表被访问的边的后顶点，比如：1: 	  
    (0, 1, 5)，代表1这个顶点被访问过，这个顶点的边为0,1，权值为5,由于最小生成树最多访问n个顶点，所以
    一开始这个列表只有起始顶点，之后访问到的就为在该顶点中加入与顶点相连的前一个线段，没访问到的就是
    None
    """
    mst={i:None for i in range(vnum)}
    cross_edge=prioQueue([(0,v,v)],reverse=True) #进行入队时，边和点的集合为w，vi,vj，这时为了进行排序操作
    count=0
    while count<vnum and not cross_edge.is_empty():
        #print("进入循环")
        w,u,v=cross_edge.dequeue()
        #如果弹出的这个边的前继顶点被访问过，继续执行出队操作，否则执行下面的操作
        if mst[v]: #当mst[v]不为None
            continue
        mst[v]=(u,v,w)
        count+=1
        for w,vi,vj in g.adjiterator(g,v).iterator_edg():
            #print(vi,vj,w)
            if not mst[vj]:
                #print((w,vi,vj))
                cross_edge.enqueue((w,vi,vj))
        #print(cross_edge.prio_list)
    return mst
print(prim(graph_1,0))
print(prim(graph_1,1))

结果：

总结：采用优先队列选取最小权值的边，这个要用到排序，由于里面记录了所有的边，所以时间复杂度为Elog(E).
(2)prim算法的优化
我们在进行上面的算法进行prim算法时，我们设置了优先队列，condas，同时发现了一个问题，即我们每次都要进行入队与出队操作时将很多没有价值的边都归入了进去。即我们的时间复杂度的开销最坏为0(E),E为图中的所有边，而我们最小生成树，可能只需要n-1个边，所以我们可以优化空间复杂度，cross_edge中边的个数减至n-1.这就要使用我们的最小索引堆。
我们设置每个边后顶点的最小权值边的最小索引堆，如果在扩展的子树中发现了更小的边，我们将其更改，并每次弹出最小索引堆中的最小权值的边。
代码实现：
1、最小索引堆的代码：

class min_index_heap():
    def __init__(self):
        self.indexlist=[0]
        self.items={ }
        self.size=0
    def insert(self,k,value):
        self.indexlist.append(k)
        self.items[k]=value
        self.size+=1
        self.perup(self.size)
    def perup(self,i):
        currentvalue=self.items[self.indexlist[i]][2]
        currentindex=self.indexlist[i]
        while i//2>0:
            if self.items[self.indexlist[i//2]][2]>currentvalue:
                self.indexlist[i],self.indexlist[i//2] = self.indexlist[i//2],self.indexlist[i]
                i=i//2
            else:
                break
    def delmin(self): #即删除最小索引堆中的最小的元素（堆中的第一个元素）
        if self.size==1: #索引堆只有一个元素：
            self.size-=1
            return self.items.pop(self.indexlist.pop())
        else:
            self.indexlist[-1],self.indexlist[1] = self.indexlist[1], self.indexlist[-1]
            u=self.indexlist.pop()
            del_element=self.items.pop(u)
            self.size-=1
            self.perdown(1)
            return del_element
    def perdown(self,i):
        while 2*i<=self.size:
            mc=self.minchild(i)
            if self.items[self.indexlist[i]][2]>self.items[self.indexlist[mc]][2]:
                self.indexlist[i],self.indexlist[mc]=self.indexlist[mc],self.indexlist[i]
                i=mc
            else:
                break
    def minchild(self,i):
        if 2*i+1>self.size: #只有左枝没有右枝
            return 2*i
        else:
            if self.items[self.indexlist[2*i]][2]>=self.items[self.indexlist[2*i+1]][2]:
                return 2*i+1
            else:
                return 2*i
    def buildheap(self,items):
        self.items=items
        self.indexlist=[0]+list(self.items.keys())
        self.size=len(items)
        i=self.size//2
        while i>0:
            self.perdown(i)
            i-=1
    def get_items(self,i):
        return self.items[i]
    def min_item(self):
        return self.items[self.indexlist[1]]
    def change(self,k,value):
        if k not in self.items:
            print("错误无法更改")
        else:
            self.items[k]=value
            i=self.indexlist.index(k) #选出索引编号为k的索引在索引堆中的位置
            self.perup(i)  #先将这个索引堆中编号k的索引向上调整位置，维护最小堆
            self.perdown(i) #再将索引堆中编号为k的索引向下调整位置，维护最小堆
            print("元素改变成功")

这个最小索引堆的代码，是根据前面最小索引堆的代码更改的，这里主要把数据的存储改为了vi,vj,w即前顶点、后顶点、权值三个部分。然后将perdown、perup中的值的比较改为了权值w的比较。
2、prim改进算法的代码

def prim2(g,v):
    #传入两个参数，图的名字、从哪个顶点生成最小生成树
    vnum=g.numvertix
    mst={i:None for i in range(1,vnum+1)} #记录最小生成树
    #print(mst)
    cross_edge=min_index_heap()
    cross_edge.items={i:None for i in range(1,vnum+1)}
    #初始化mst和cross_edge
    cross_edge.insert(v,[v,v,0])
    count=0
    while count<vnum:
        min_edge=cross_edge.delmin()
        #print(min_edge)
        v=min_edge[1]
        mst[v]=min_edge
        #print(mst)
        for w,vi,vj in g.adjiterator(g,v).iterator_edg():
            if vj not in cross_edge.items:
                continue
            else:
                if cross_edge.items[vj] is None:
                    cross_edge.insert(vj,[vi,vj,w])
                else:
                    ori_edge=cross_edge.get_items(vj)
                    if ori_edge[2]<=w:
                        pass
                    else:
                        cross_edge.change(vj,[vi,vj,w])
        #print(cross_edge.items)
        #print(cross_edge.indexlist)
        count+=1
    return mst
graph_2=sparsegraph(directed=False)
graph_2.addedge(1,2,5)
graph_2.addedge(1,4,5)
graph_2.addedge(2,4,3)
graph_2.addedge(2,7,7)
graph_2.addedge(2,5,9)
graph_2.addedge(5,7,8)
graph_2.addedge(6,7,8)
graph_2.addedge(3,6,6)
graph_2.addedge(1,3,11)
graph_2.addedge(3,4,7)
graph_2.addedge(4,7,20)
print(prim2(graph_2,1))
print(prim2(graph_2,2))

代码解析：其中由于最小索引堆是从1开始的，所以我进行图的建造也是从1开始的，测试数据如下图所示：

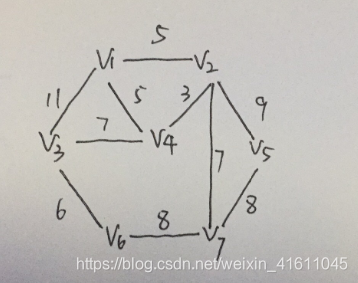
数据循环如下面两个图所示：


最终程序运行的结果：

可以看出，最小生成树运行成功，并且空间占用最多只有O(E)，时间为logE（因为是索引堆的缘故）
二、最短路径问题
1、什么是最短路径
这里讨论的是带权有向图和带权无向图，在这类图中一个顶点到其他顶点可能有路径，可能没有路径，也可能有多条不同的路径，怎样找到一条最好的路径呢，这就是本节要讨论的最短路径问题。
定义：
在图中：

• 从顶点v到 $v^`$的各个边的长度之和就称为该路径的长度。
• 从v到 $v^`$的所有长度中最短的路径就是v到 $v^`$的最短路径，最短路径记为dist(v,v`)
  在介绍之前我们要先明确几个概念 （1）最小生成树（2）最短路径树（3）最短路径
  （1）最小生成树
  将最少的边集将一个图连成任意2点可达，并且这个边集的总长度最小。保证整个拓扑图的所有路径之和最小。通常用Prim算法和kruskal算法求解。
  （最小生成树是指图中一点到其他所有顶点的总和最小）
  （2）最短路径树
  最短路径树是指，图中一点到其他所有点的最短路径构成的树
  （3）最短路径
  最短路径是指图中任意两点形成的最短路径
  
  2、最短路径树
  最短路径树，又称为单源最短路径树，是指从图中一个顶点出发，到其他任意顶点的最短路径构成树的集合
  算法概要：
  1、将图中顶点分为两个集合，当时已知的最短路径的集合U,和尚不知道的最短路径的集合V-U
  2、在集合U中放入顶点v0，v0到v0的距离的为0
  3、对V-U的每个顶点v，如果存在v和v0相连的话，则将其v0-v的权值w设为已知的权值w，否则设为None.
  不断重复：
• 从V-U中选出当时已知的最段路径的顶点 $v_{min}$加入U,
• 由于 $v_{min}$的加入，V-U中的已知的最短路径可能发生改变，如果从v0到 $v_{min}$到 $v`$的路径比以前已知的路径的更短，则更新 $v`$ 的最短路径的距离记录，保证能继续在V-U中挑选顶点。

看完了，还是有点晕还是来看例子吧。

时间复杂度：O(Elog(v))
我们以一个例子来看看dijkstra的具体实现：




代码实现：
辅助函数：
这里的辅助函数包括，图的实现、最小索引堆

#顶点类实现的代码
class vertix():
    #vertix有两个属性：id，这个结点的名字和connected_to有联系的边和权值组成的集合
    def __init__(self,key):
        self.id=key
        self.connect_to={ }
    def addneighbor(self,nbr,weight):
        self.connect_to[nbr]=weight
class sparsegraph(object):#采用邻接表的表示方式实现图
    #基础属性：vertixlist:顶点的集合，directed：是有向图还是无向图
    def __init__(self,directed=False):
        self.vertixlist={}
        self.numvertix=0
        self.directed=directed
    def addVertix(self,key):
        """添加名字为key的顶点，我们添加完后，其顶点的合集为{顶点1：vertix类，顶点2：vertix类}"""
        newvertix=vertix(key)
        self.vertixlist[key]=newvertix
        self.numvertix+=1
        return newvertix
        # 为邻接矩阵添加边,在v和w之间添加一条边
    def addedge(self, v, w, cost=0):
        if v not in self.vertixlist:
            self.addVertix(v)
        if w not in self.vertixlist:
            self.addVertix(w)
        if self.directed:
            self.vertixlist[v].addneighbor(w, cost)
        else:  # 如果是无向图
            self.vertixlist[v].addneighbor(w, cost)
            self.vertixlist[w].addneighbor(v, cost)
#最小索引堆的代码
class min_index_heap():
    def __init__(self):
        self.indexlist=[0]
        self.items={ }
        self.size=0
    def insert(self,k,value):
        self.indexlist.append(k)
        self.items[k]=value
        self.size+=1
        self.perup(self.size)
    def perup(self,i):
        currentvalue=self.items[self.indexlist[i]][2]
        currentindex=self.indexlist[i]
        while i//2>0:
            if self.items[self.indexlist[i//2]][2]>currentvalue:
                self.indexlist[i],self.indexlist[i//2] = self.indexlist[i//2],self.indexlist[i]
                i=i//2
            else:
                break
    def delmin(self): #即删除最小索引堆中的最小的元素（堆中的第一个元素）
        if self.size==1: #索引堆只有一个元素：
            self.size-=1
            return self.items.pop(self.indexlist.pop())
        else:
            self.indexlist[-1],self.indexlist[1] = self.indexlist[1], self.indexlist[-1]
            u=self.indexlist.pop()
            del_element=self.items.pop(u)
            self.size-=1
            self.perdown(1)
            # 注，这里的del_element是一个集合即 4：（1,4,2），del_element=1,4,2线段的起点和终点及权值
            return del_element
    def perdown(self,i):
        while 2*i<=self.size:
            mc=self.minchild(i)
            if self.items[self.indexlist[i]][2]>self.items[self.indexlist[mc]][2]:
                self.indexlist[i],self.indexlist[mc]=self.indexlist[mc],self.indexlist[i]
                i=mc
            else:
                break
    def minchild(self,i):
        if 2*i+1>self.size: #只有左枝没有右枝
            return 2*i
        else:
            if self.items[self.indexlist[2*i]]>=self.items[self.indexlist[2*i+1]]:
                return 2*i+1
            else:
                return 2*i
    def buildheap(self,items):
        self.items=items
        self.indexlist=[0]+list(self.items.keys())
        self.size=len(items)
        i=self.size//2
        while i>0:
            self.perdown(i)
            i-=1
    def get_items(self,i):
        return self.items[i]
    def min_item(self):
        return self.items[self.indexlist[1]]
    def change(self,k,value):
        if k not in self.items:
            print("错误无法更改")
        else:
            self.items[k]=value
            i=self.indexlist.index(k) #选出索引编号为k的索引在索引堆中的位置
            self.perup(i)  #先将这个索引堆中编号k的索引向上调整位置，维护最小堆
            self.perdown(i) #再将索引堆中编号为k的索引向下调整位置，维护最小堆
            #print("元素改变成功")

(2)dilkstra算法代码实现

def dilkstra(g,v):
    # 保存每个顶点到开始顶点的最短距离
    distance={ }
    # 记录从startpoint开始到末尾的所有顶点的前一个顶点
    path={ }
    #采取最小索引堆的方式来进行最小边的扩充
    min_indexheap=min_index_heap()
    min_indexheap.insert(v,(v,v,0))
    path[v]=v
    distance[v] = 0
    count=0
    while count<g.numvertix or len(min_indexheap.items)!=0:
        #弹出顶点、权值
        #print(min_indexheap.items)
        del_ment=min_indexheap.delmin()
        v1,v2,w=del_ment[0],del_ment[1],del_ment[2]
        #print(v1,v2,w)
        distance[v2]=w
        path[v2]=v1
        #g.vetixlist中存储的是各个顶点的对象，分别是顶点的id和与之相邻的边，如{1：顶点1的集合，顶点
        #1.id=1，顶点1.conncet_to={2:3,4:3}}
        for v2_connect in g.vertixlist[v2].connect_to:
            if v2_connect not in min_indexheap.items : #这个顶点没有被访问过
                if v2_connect not in distance: #如果这个顶点还没有找到最短路径
                    w1=g.vertixlist[v2].connect_to[v2_connect]
                    w2=distance[v2]
                    w=w1+w2
                    #print(v2, v2_connect,w)
                    min_indexheap.insert(v2_connect,(v2,v2_connect,w))#起点、终点、权值
            else: #这个顶点已经被访问过，看是否存在更短路径
                w1=min_indexheap.items[v2_connect][2]
                w2=g.vertixlist[v2].connect_to[v2_connect]
                w3=distance[v2]
                w=min(w1,(w2+w3))
                min_indexheap.change(v2_connect,(v2,v2_connect,w))
        #print(min_indexheap.items)
        count+=1
    print(distance)
    print(path)

##测试代码
graph1=sparsegraph(directed=False)
graph1.addedge(1,4,2)
graph1.addedge(1,3,5)
graph1.addedge(4,5,6)
graph1.addedge(3,5,2)
graph1.addedge(3,6,7)
graph1.addedge(5,7,2)
graph1.addedge(6,7,3)
graph1.addedge(2,6,4)
graph1.addedge(3,2,3)
graph1.addedge(2,3,4)
graph1.addedge(2,1,11)
print("########################dijsktra算法#################################")
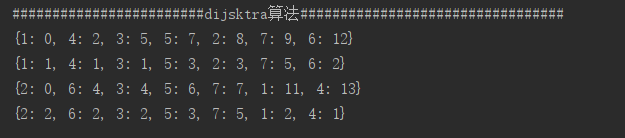
dilkstra(graph1,1)
dilkstra(graph1,2)

结果：

最短单源路径是，从一个顶点到其他顶点路程最短，最小生成树是从一点到其他所有点的路径长度加起来最小，两者是有区别的
方法2：采用优先队列
方法1，采用最小索引堆的空间复杂度和时间复杂度虽然低，但是我们要先写最小索引堆，所以下面介绍通过优先队列的方式进行Dijkstra算法的实现。

#最小优先队列
class prioQueue:
    def __init__(self,elist=[],reverse=True):
        self.prio_list=list(elist)
        self.reverse=reverse
        self.prio_list.sort(reverse=self.reverse)
    def enqueue(self,e): #入队列
        i = len(self.prio_list) - 1
        #如果元素中小的为优先级
        if self.reverse==True:
            while i>=0:
                if self.prio_list[i][0]<=e[0]:
                    i-=1
                else:
                    break
            self.prio_list.insert(i+1,e)
        else: #最大的优先级
            while i>=0:
                if self.prio_list[i][0]>=e[0]:
                    i-=1
                else:
                    break
            self.prio_list.insert(i+1,e)
    def is_empty(self):
        if self.prio_list == []:
            return True
        else:
            return False
    def dequeue(self): #出队
        if self.is_empty():
            print("队列为空，无法出队")
            return
        else:
            return self.prio_list.pop()
def dijkstra2(g,v):
    vnum=g.numvertix
    assert 0<=v<vnum
    path=[None] * vnum
    count=0
    candas=prioQueue([(0,v,v)],reverse=True)
    while count<vnum and not candas.is_empty():
        w1,u,vmin=candas.dequeue()
        if path[vmin]:
            continue
        path[vmin]=(u,w1)
        for v in g.vertixlist[vmin].connect_to:
            w=g.vertixlist[vmin].connect_to[v]
            if not path[v]:
                candas.enqueue((w1+w,vmin,v))
        count+=1
    print(path)
graph2=sparsegraph(directed=True)
graph2.addedge(0,3,2)
graph2.addedge(0,2,5)
graph2.addedge(3,4,6)
graph2.addedge(2,4,2)
graph2.addedge(2,5,7)
graph2.addedge(4,6,2)
graph2.addedge(5,6,3)
graph2.addedge(1,5,4)
graph2.addedge(2,1,3)
graph2.addedge(1,2,4)
graph2.addedge(1,0,11)

dijkstra2(graph2,0)

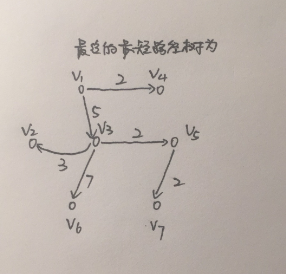
这里参数的结果的意思是：（0，0，0）代表顶点0的前一个顶点为0，从开始顶点到0的最短路程为0，（2，1，8）的意思是顶点1的前一个顶点的为顶点2，从开始顶点到顶点1的最短距离为8，以此类推。
整个的过程如下所示：


3、dilkstra的二维矩阵表示：

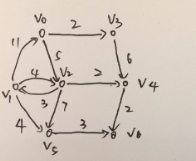
算法步骤:
（1）选取一个初始顶点（比如顶点0）
（2）用path记录各个顶点的最短路径{0：None，1：None…6:None}，用queue记录优先队列
（3）将0相连的边加入优先队列，并记录顶点的上一个位置和最短路径，比如0而言queue=([3,0,2],[2,0.5]),代表2的上一个顶点为0，最短距离为5，3的上一个顶点为0，最短距离为2
（4）弹出一个优先队列距离的最小值，将其记录在path中，这里要看这个顶点的前一个顶点是否已经找到最短路径了，如果找到了则直接用顶点加上这个弹出的边记录为最短路径加入path,如果这个边的前一个顶点在path中为None,则只需要将这个边加入队列中。将并将这个队列的相邻顶点继续加入优先队列。
（5）重复（3）(4)path中所有的顶点都不为None
其实这一算法的思想是，不断构建最短路径树，且每次都保证从已经构建完成后的最短路径树中取出最小的横切边来继续生成最短路径树。