数学公式整理

1.各种数：

　　全排列：P(n,n)=n!    部分排列：P(n,m)=n!/(n-m)!

　　组合数：公式：C(n,m)=n!/(m!*(n-m)!)   递推式 :C(n,m)=C(n-1,m)+C(n-1,m-1)  

　　　　　　Lucas定理：C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p

　　　　　　

#define long long LL 
//farc[i]表示i！ 
LL C(LL n,LL m,LL p){
    if(n<m)return 0;
    return farc[n]*fpow(farc[m],p-2,p)%p*fpow(farc[n-m],p-2,p)%p;
}
LL Lucas(LL n,LL m,LL p){
    if(n<m)return 0;
    if(!n)return 1;
    return Lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

Lucas

　　　　　　性质/应用：1.C(n,m)=C(n,n-m)

　　　　　　 　　　　　2.二项式定理：

　　　　　　　　　　　 3.m*C(n,m)=n*C(n-1,m-1)，

　　　　　　　　　　　 4.C(n,1)²+C(n,2)²+C(n,3)²+...+C(n,n)²=C(2n,n)

　　圆排列: Q(n,n)=（n-1)!   n个人坐成一圈有多少种坐法。

　　　　　  Q(n,m)=P(n,m)/m=n!/(m*(n-m)!)   部分圆排列　　

　　重复排列(有限个)：n!/(a1!*a2!*…*ak!)  k种不一样的球，每种球的个数分别是a1,a2,...ak,设n=a1+a2+…+ak，求这n个球的全排列数。

　　重复组合(无限个):  C(n+k-1,k) 　　　  n种不一样的球，每种球的个数是无限的，从中选k个出来的方案数。

　　不相邻组合：C(n-k+1,k)  1~n这n个自然数中选k个，这k个数中任何两个数不相邻数的组合有多少种。

　　错排(错位排列)：d(n)=(n-1)*(dn-1 + dn-2)，n≥3

　　stirling数: 第一类：S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m)    n个不同元素构成m个圆排列的方案数

　　　　　　　第二类：S(n,m)=S(n-1,m-1)+m*S(n-1,m).       n个不同元素构成m个非空的(无差别)集合的方案数

　　Catalan数：通项式：H(n)=C(2n,n)/(n+1)=(2n)!/( (n+1)!*n!)

　　　　　　　　　　　  Hn=C(2n,n)-C(2n,n-1)

　　　　　　　  递推式：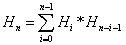

　　部分转载自：https://www.cnblogs.com/ljc20020730/p/11302718.html　　　

　　　　　　　　https://blog.csdn.net/qq_36808030/article/details/75045129　　　　　

2.其他：

　　约瑟夫问题： 假设编号从0开始   F(i)表示在有i个人参与下 报数为m时 最后获胜的玩家编号 f[1]=0 ，f[i]=(f[i-1]+m) % i ，(i>1）

　　　　　　　　 报数为2时 J(g)表示g个人参与下最终获胜的人的编号   设g=2**t+x (2t>x 且 x≥0) 则 J(g)=2x+1​     2**t为不超过g的最大的二次幂

　　　　　　　　一道约瑟夫问题的好题：罗德岛裁员