Euler’s Formula 关于欧拉公式的理解
1 前言(废话)
在看一些雷达相关的论文,从复信号开始迷糊,一连串的迷糊下来,迷糊到了欧拉公式。看到了BetterExplained的文章Intuitive Understanding Of Euler’s Formula解释的好妙啊!!作为一个孤陋寡闻的数学渣,俺被刷新了认知,一边看一边感叹,竟然觉得好有意思...真是这辈子少有的体验哈哈。
一开始想翻译来着,查了一下未经授权翻译是侵权。所以,在此复述一些我觉得比较重要的观点,分享一下哈,这应该不算侵权吧(查不到复述外文主要观点算不算侵权,如果算,希望可以提醒一下哈)。不过,还是推荐看原文,讲的很全面。
2 预备知识
在理解欧拉公式之前,我认为还需要对复数、指数增长有基本的理解。暂时没有去搜索中文的文章,在此放上BetterExplained的文章的传送门,可挑选部分关键的看(比如带图的部分):
- 复数的理解:A Visual, Intuitive Guide to Imaginary Numbers
- 怎么理解虚数和复数? - 李狗嗨的回答 - 知乎
- 指数函数及e的理解:An Intuitive Guide To Exponential Functions & e
搬运重要的结论:
\(e\)的定义:
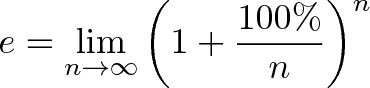
指数函数的理解:
在\(1\)的基础长,以\(r\)的增长率,持续增长\(t\)的时间,最后总的增长量是\(e^{r\cdot t}\)。注意持续增长的理解,要与日常语境中的意义区分。
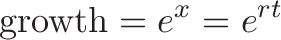
3 概述
欧拉公式:
\[e^{ix} = cos(x) + i sin(x) \]
欧拉公式描述了什么?作者如是说:
Euler's formula describes two equivalent ways to move in a circle.
欧拉公式使用了2种等价的方法(即等式的左边和右边),来描述在一个圆弧上的运动。就是说,它描述了旋转运动。怎么理解呢?下文会分别对公式的左边和右边进行解释。
PS:值得注意的是,公式中等号的意义。在数学中,等号存在一定的歧义,它可以表示:1. 赋值;2. 等价(这种歧义在高级语言中就不存在啦)。欧拉公式中等号的意义是后者。
4 对\(e^{ix}\)的理解
可以从以下几个方面来理解:
- 整体来看,把 \(e^{ix}\) 看作 \(1\cdot e^{ix}\) ,把乘法看作一种变换,这个式子就可以理解为对\(1\)做\(e^{ix}\) 变换。
- 对于指数的理解:
- 先回到熟悉的实数 \(1\cdot e^{3}\),对于这个式子,我们可以理解为在\(1\)的基础上以\(r\)的增长率,\(t\)的时间持续增长,其中\(r\cdot t = 3\)。所以“实指数增长”我们可以理解为:在\(1\)的基础上,以某个增长率,持续地增长某段时间。
- “虚指数增长”就可以理解为:让\(1\)持续地旋转某段时间。
- 增长\(x\)个单位时间,就可以理解为沿着圆弧运动\(x\)
- \(e^{ix}\)就可以理解为,从\(1\)开始,旋转\(x\)弧度
以 \(x=\pi\) 时这个特殊情况为例。代入可得下式:
\[e^{i\pi} = -1 \]
对于式子\(e^{i\pi} = -1\)就可以理解为,从1开始,旋转\(\pi\)得到-1
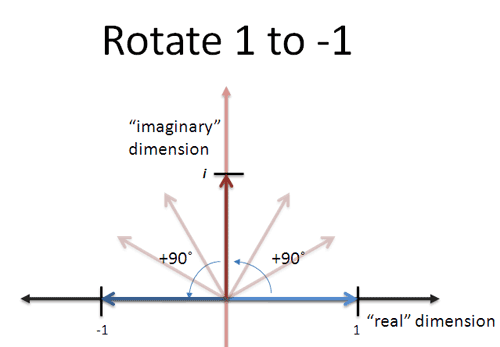
图源:BetterExplained
* “虚指数增长”
先从实数开始考察,以 \(3^{4}\) 为例:
- 换一种方式来看底数 3:\(3 = e^{ln(3)}\),即把3看作以\(ln(3)\)的增长率持续增长的结果(在1的基础上,增长1个单位时间)
- 那么\(3^{4}\) ,就可以看作以相同的增长率\(ln(3)\)持续性地增长4倍长的时间
- 实指数的增长,即在原来的基础上,在“实”方向(与原方向同向)上拉长。
回到“虚“指数增长,则是在“虚”方向(与原始方向垂直的方向)旋转,且仅仅是旋转。
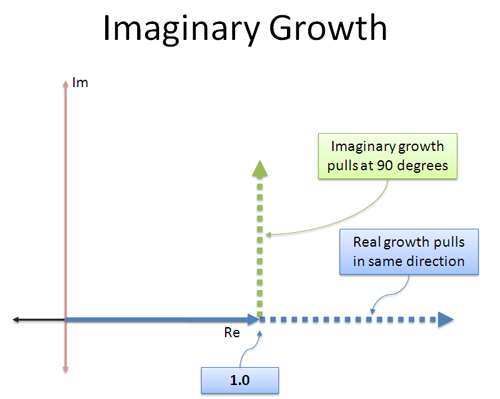
图源:BetterExplained
5 对\(cos(x) + i sin(x)\)的理解
对于等式右边,典型的复数,对复数稍微有一些了解就非常容易理解。
暂不赘述了。
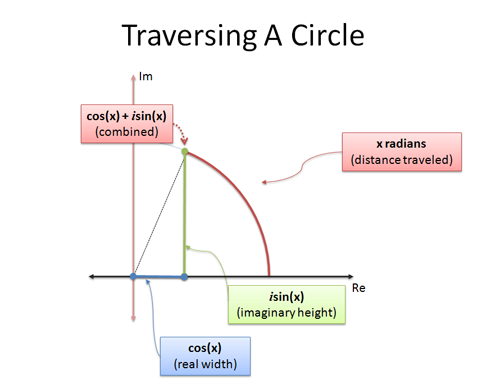
图源:BetterExplained
6 结语
没有完全照搬原文的结构,按照自己的理解重新梳理了一下,若有错误或者不恰当的地方,请批评指正。