本博文为本人的学习笔记，仅供本人学习记录哈，部分资料参考了网上的其他博客，也在文末给出了引用。

离散系统的输出响应

信号的能量与功率

欧拉公式

傅里叶变换

连续时间信号的傅里叶分析

连续周期信号的傅里叶级数（Fourier Series）

信号的分类

按照信号随时间变化的特点分类

随机信号：描述的物理过程具有不可重复性和不可预测性，但有统计特征。

显然，现代信号处理理论以及通信系统中，主要研究随机信号的处理。

单位抽样信号（Kronecker 函数）

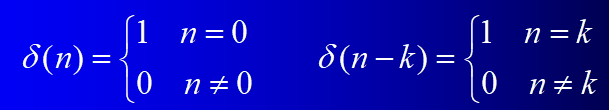
离散信号

clear all
t=0:0.1:2*pi;%给定一系列离散的点
x=cos(2*t);%cos连续信号的离散抽样
stem(t,x);%stem(Y) 将数据序列Y从x轴到数据值按照茎状形式画出,以圆圈终止。

离散系统的输出响应

clear all
n=0:60;
x=exp(-0.2*n);%%%为输入信号
h=exp(-0.1*n);%%%系统的响应
y=conv(x,h);%%%%离散线性移不变系统的输出响应
subplot(3,1,1);stem(x);title('x 输入信号');
subplot(3,1,2);stem(h);title('h 信道响应')
subplot(3,1,3);stem(y);title('y 系统的输出响应')

信号的能量与功率

欧拉公式

作为时间函数的复数和称为正交信号。

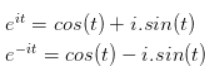
对于欧拉公式，当其等于pi时，有：

欧拉公式的作用：

简化了数学推导和分析过程，将一个三角方程转化为一个用指数表示的简单代数式，使复数的数学运算几乎采用与实数一样的规则进行；
使得信号的相加简化为复数相加；
它是复数的最简洁表示；
它是有关数字通信系统如何设计、描述的主要形式。

实数轴与虚数轴共同构成了一个复数的平面，也称复平面。乘虚数i的一个功能——旋转，将数据从实数轴变换到虚数轴

欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。

由此可以知道：正弦波的叠加，也可以理解为螺旋线的叠加在实数空间的投影。

傅里叶变换

之学数字信号处理的时候，对傅里叶变换理解得比较深入的，但是后面又忘掉了，这里就写一写关于傅里叶变换的学习理解哈~

我们经常接触到的信号，正弦信号，余弦信号，甚至是复杂的心电图、脑电图、地震波信号都是时域上的信号，我们也成为原始信号，但是通常情况下，我们在原始信号中得到的信息是有限的，所以为了获得更多的信息，我们就需要对原始信号进行数学变换，得到变换域的信号，通常接触到的变换主要有傅里叶变换、拉普拉斯变换、Z变换、小波变换等等，这里主要讨论下傅里叶变换。

根据信号的不同类型，可以把傅立叶变换分为四类：

1) 非周期性连续信号：傅立叶变换(Fourier Transform，FT)

2) 周期性连续信号：傅立叶级数(Fourier Series，FS)

3) 非周期性离散信号：离散时域傅立叶变换(Discrete Time Fourier Transform ,DTFT)

4)周期性离散信号：离散傅立叶变换(Discrete Fourier Series，DFS)

这四种傅立叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，我们知道这对于计算机处理来说是不可能的，那么有没有针对长度有限的傅立叶变换呢？没有。因为正余弦波被定义成从负无穷小到正无穷大，我们无法把一个长度无限的信号组合成长度有限的信号。

面对这种困难，方法是：把长度有限的信号表示成长度无限的信号。如，可以把信号无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性离散信号，我们可以用到离散时域傅立叶变换（DTFT）的方法。也可以把信号用复制的方法进行延伸，这样信号就变成了周期性离散信号，这时我们就可以用离散傅立叶变换方法（DFT）进行变换

由上图可以看出，若x在时域是周期的，那么在频域X一定是离散的。同样的，若x是非周期的，X一定是连续的。

连续时间信号的傅里叶分析

傅里叶分析可以分为傅里叶变换与傅里叶级数。一般情况下，若“傅里叶变换”一词不加任何限定语，则指的是“连续傅里叶变换”。

1822年，fourier指出，任意一个周期函数x(t)都可以分解为无穷多个不同频率的正弦信号的和，即傅里叶级数。而求解傅里叶系数的过程就是傅里叶变换。傅里叶级数和傅里叶变换又称为傅里叶分析或谐波分析。

通过下面的讨论分析可知，傅里叶变换实际上是将信号x(t)和一组不同频率的复正弦作内积，这一组复正弦即变换的基向量，而傅里叶系数或傅里叶变换是x(t)在这一组基向量上的投影

首先给出系列书本的理论

连续周期信号的傅里叶级数（Fourier Series）

傅里叶告诉我们：任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。

设是复周期信号，且是周期的，周期为,则能展开为傅里叶级数：

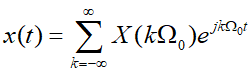
对应的傅里叶系数为：

注意：傅里叶级数反映傅里叶的基本思想与观点：即任意函数可由正弦函数合成，例如看到矩形函数想到的是一系列正弦函数。

傅里叶级数需要满足Dirichlet条件：

矩形周期信号及其傅里叶系数

连续非周期信号的傅里叶变换

设是连续时间信号，且

傅里叶变换定义为：

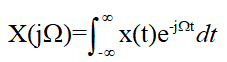
或写为式中，=2*pi*f为角频率，单位是rad/s。其中是的连续函数，称为信号x(t)的频谱密度函数或简称为频谱。

可以把傅里叶变换也成另外一种形式：

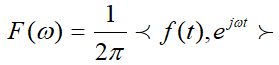
可以看出，傅里叶变换的本质是内积，三角函数是完备的正交函数集，不同频率的三角函数的之间的内积为0，只有频率相等的三角函数做内积时，才不为0。（如下式所示，只有两个频率相等时，单位抽样信号才不为0）

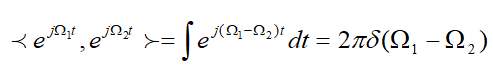
因为傅里叶变换的本质是内积，所以f(t)和求内积的时候，只有f(t)中频率为的分量才会有内积的结果，其余分量的内积为0。可以理解为f(t)在上的投影，积分值是时间从负无穷到正无穷的积分，就是把信号每个时间在的分量叠加起来，可以理解为f(t)在上的投影的叠加，叠加的结果就是频率为的分量，也就形成了频谱。

傅里叶反变换为：

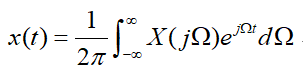
或写为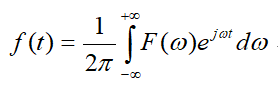

傅里叶逆变换就是傅里叶变换的逆过程，在和求内积的时候，只有t时刻的分量内积才会有结果，其余时间分量内积的结果为0，同样积分值是频率从负无穷到正无穷的积分，就是把信号在每个频率在t时刻上的分量叠加起来，叠加的结果就是f(t)在t时刻的值，这就回到了我们观察信号最初的时域。

对一个信号做傅里叶变换，然后直接做逆变换，这样做是没有意义的，在傅里叶变换和傅里叶逆变换之间有一个滤波的过程。将不要的频率分量给滤除掉，然后再做逆变换，就得到了想要的信号。比如信号中掺杂着噪声信号，可以通过滤波器将噪声信号的频率给去除，再做傅里叶逆变换，就得到了没有噪声的信号。

注意：傅里叶变换是频谱密度的概念。

傅里叶变换与傅里叶级数的区别

图像傅里叶变换的意义

后面本人会发表一篇paper，是关于图像的傅里叶变换在VLC中的应用。在此先对图像做傅里叶变换的意义进行一下理解分析。

首先，对于图像而言，图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。

从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅立叶变换是将图
像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

傅立叶频谱图上我们看到的明暗不一的亮点，其意义是指图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅立叶变换后的频谱图，也叫功率图，我们就可以直观地看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的、边界分明且边界两边像素差异较大的。

代码

给出连续函数的傅里叶变换的代码

clear all
syms t;
f=t*exp(-abs(t));
subplot(2,1,1);ezplot(f);%title('f(t)')
%%%%%%%%%%%函数ezplot它无需数据准备，直接画出函数图形，基本调用格式为ezplot(f)，其中f 是字符串或代表数学函数的符号表达式，只有一个符号变量
F=fourier(f)
subplot(2,1,2);ezplot(abs(F));%title('F(w)')

傅里叶逆变换

clear all
syms t w;
F=pi*exp(-abs(w));
subplot(1,2,1); ezplot(abs(F));
f=ifourier(F,t)
subplot(1,2,2); ezplot(f)

下面本来打算仿真一个复杂一点的函数的傅里叶变换，但是不知道为啥频谱出bug了，有小伙伴懂的请赐教哈~

clear all
syms t v w x f(t);
% f=t*exp(-abs(t));
f(t)=cos(2*pi*5*t)+cos(2*pi*10*t)+cos(2*pi*20*t)+cos(2*pi*50*t);
subplot(2,1,1);ezplot(f);%title('f(t)')

y = fourier(f(t),t); 
subplot(2,1,2);ezplot(y);%title('F(w)')xlim()

出来的频谱竟然为0？？？！！！

傅里叶级数和傅里叶变换的区别与联系

傅里叶级数对应的是周期信号。傅里叶级数的系数是离散的。代表周期信号x(t)的第k次谐波幅度的大小。

傅里叶变换对应的是非周期信号。傅里叶变换是的连续函数。是频谱密度的概念。何为频谱密度呢？请看下面解释：

由上述讨论，我们可以得知：时域连续的周期信号的傅里叶变换在频域是离散的，非周期的。而当周期信号的周期T趋于无穷大时（实际上，这个周期信号就变成了非周期信号），而对应的离散的频谱叶变成了连续谱。故此，可以得到：时域连续的非周期信号的傅里叶变换在频域上时连续的，非周期的。

进一步理解傅里叶级数

以时间来衡量的称为时域，以频率来衡量的称为频域。而时间是一直在变换的，所以我们说世界一直在变化，但是频域上的世界却是可以不变的。

时域的基本单元就是“1 秒”，如果我们将一个角频率为 $\omega_{0}$ 的正弦波看作基础，那么频域的基本单元就是 $\omega_{0}$

其中，就是一个周期无限长的正弦波，也就是一条直线！所以在频域，0 频率也被称为直流分量，在傅里叶级数的叠加中，它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。

正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆

一个矩形波在频域的样子如下图所示：（可以发现，在频谱中，偶数项的振幅都是0，也就对应了图中的彩色直线。振幅为 0 的正弦波。）

很多在时域看似不可能做到的数学操作，在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。

通过时域到频域的变换，我们得到了一个从侧面看的频谱，但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每一个对应的正弦波的振幅是多少，而没有提到相位。基础的正弦波A.sin(wt+θ)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱（振幅谱）是不够的，我们还需要一个相位谱。

时间差并不是相位差。如果将全部周期看作2Pi或者360度的话，相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi，就得到了相位差。