数据结构图、算法相关文章:
《算法笔记》—— 图 “邻接矩阵” 的遍历(DFS、BFS)
此文中也链接着其它一系列的图相关的文章 . . .
.
现实之中,我们往往会使用百度地图等一系列的地图软件,当我们选择一个目的地时,这些软件会给我们匹配一个最佳的路线,也就是最近的路线,例如下面这个图:
那么这些算法是如何实现的呢 ? 下面我们一起来学习一下吧 . . . ^_^
.
此文将讲述两个重要的算法,他们分别用于 “多源最短路径” 与 “单源最短路径” 问题 . . . 至于什么是多源什么是单源我们将在下面讲解 . . .
.
Floyd-Warshall算法
有的时候,我们住在一个城市之中,想知道任意两个地方的最短路径是多少,“任意” 两字就引发了这个 “多源最短路径” 问题,多源就是指多个起点到不同的终点 . . .
例如下面的这个图:

其中圆圈表示一个城市(地方)、线上的数字表示路程、线的箭头表示这是一个有向图 . . .
为了方便的解决这个多源问题,我们用 邻接矩阵来存储这个图的数据,如下图所示:
这个数组名为 e ,其中的 * 表示两个城市的最短路径求知 . . .
.
算法核心思想
—— 如果想求出最短路径是多少,必须判断当前的顶点(城市)到目标顶点(城市)有没有经过其它的顶点,如果有,则判断经过的顶点是否小于当前顶点直接到目标顶点的距离 . . .
例如,我们想知道任意两个顶点(城市)经过顶点1 所需要的最短路径是多少,我们
只需要判断 e[i][1] + e[1][j] 是否比 e[i][j] 要小 即可。
为什么需要这样判断呢? 让我细细道来,先看如下的图:

12 表示 顶点4 到 顶点3 的距离,5 表示顶点4 到
顶点1的距离,6表示顶点1到 顶点3 的距离 . . .
.
我们发现 5 和 6 这两个距离有一个顶点是他们共同的顶点1,都是和顶点1有关系的两个顶点,所以顶点4 可以通过顶点1 到达 顶点3,我们只需要判断 5 + 6 是否小于 12,如果是,则更新邻接矩阵中的数据,我们称之为最短路径 . . .
回到上面我们例出的式子, e[i][1] + e[1][j] 是否比 e[i][j] 要小,其中 i 是 1 - n循环,j 是 1 - n循环,因为我们需要的是任意两个顶点经过顶点1 的最短路径 . . .
代码实现如下所示:
for(i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
{
if(e[i][j] > e[i][1] + e[1][j])
e[i][j] = e[i][1] + e[1][j]; // 更新最短路径
}
}当我们以顶点1为中转对象,邻接矩阵的最短路程更新:

我们发现,刚刚我举的例子的 12 已经被 更新为 5 + 6了,其它两个路程也被更新为了 9、7,可以按照上面我画出的图对比一下,看是否是正确的:

我已经用橙色的画笔标明了,大家可以看看其它两个被更新的值的画法 . . . ^ _ ^
.
我们已经知道了以顶点1 为转点,那么以其它顶点为转点还用说吗?直接来一个 for循环不就行了吗,其实还真的那么简单,Floyd-Warshall算法的核心代码只有五行 . . .
核心代码如下:
for(k = 1; k <= n; k++)
for(i = 1; i <=n; i++)
for(j = 1; j <=n; j++)
if(e[i][j] > e[i][k] + e[k][j]) // 以各种顶点为转点判断
e[i][j] = e[i][k] + e[k][j]; // 更新最短路径我们把这核心的五行代码理解了,我们就能求出任意两点的最短路径,下面我们来看一下完整的代码,来演示一下这个 Floyd-Warshall算法 的使用 . . .
完整代码如下:
#include <stdio.h>
int main()
{
int inf = 9999999; // 表示 * 求知
int i, j, k;
// 第一行、第一列为0,从1开始索引 便于阅读
int e[5][5] = // 邻接矩阵,初始最短路径
{
0, 0, 0, 0, 0,
0, 0, 2, 6, 4,
0,inf, 0, 3,inf,
0, 7,inf, 0, 1,
0, 5,inf, 12, 0
};
for (k = 1; k <= 4; k++)
for (i = 1; i <= 4; i++)
for (j = 1; j <= 4; j++)
if (e[i][j] > e[i][k] + e[k][j]) // 以各种顶点为转点判断
e[i][j] = e[i][k] + e[k][j]; // 更新最短路径
for (i = 1; i <= 4; i++)
{
for (j = 1; j <= 4; j++)
printf("%d ", e[i][j]);
printf("\n");
}
return 0;
}我们求出的结果为:
0 2 5 4
9 0 3 4
6 8 0 1
5 7 10 0现在每个顶点(城市)之间已经算出了最短的路径 . . .
这是用于解决多源的算法,下面让我们来看看单源的问题吧 . . .
.
.
Diljkstra算法
“单源最短路径” 指的是指定一个点到其余各个顶点的最短路径,例如求出下图中的 1 号顶点到其余各个顶点的最短路径:

与上面一样,紫色字体表示的是两个顶点点的距离,我们还是用邻接矩阵来存储这个图中的信息,这个图的初始值如下所示:

和上面一样 * 表示的是求知的数,下面让我们来分析一下什么是 “Diljkstra算法” 算法吧
首先我们需要一个一维数组来存储 1号顶点到其余各个顶点的初始路程,如下所示:
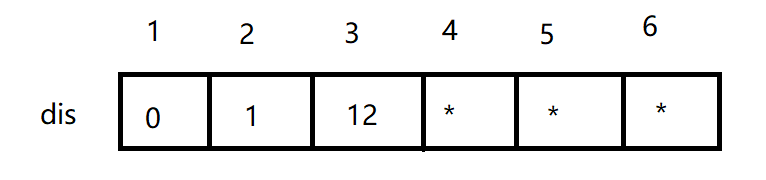
现在与顶点1 有直接联系的只有顶点 2和顶点3 . . . 其它的求知我们用 * 表示 . . .
.
算法核心思想
每次找到离源点(这个例子的源点就是 顶点1)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径 . . .
如果不理解这个算法思想,那么继续向下面看吧 . . .
算法思想解决此题方法:
- 按照这个算法思想,我们
选择 顶点2(离顶点1最近 ,长度只有 1,顶点3太远),以顶点2 为中心进行扩展,顶点2 的出边有 2 -> 3 和 2 -> 4 这两条边,我们逐一比较看看能不能使 顶点1 到 顶点3 或者顶点4 的距离变短,这个进程有个专业的术语叫做 “松弛” . . .
.- 我们先看看 2 -> 3 这条边 是否能使 顶点1 到 顶点3 的距离变短,我们现在只需要比较一下
dis[3] 和 dis[2] + e[2][3]的大小,(dis[3]表示顶点1到顶点3的距离, dis[2]表示顶点1到顶点2的距离, e[2][3]表示 顶点2 到顶点3 的距离). . .
结果是 dis[3] = 12,而 dis[2] + e[2][3] = 1 + 9 = 10,所以 dis[3] 被更新为 10,通过 2 -> 3 这条边松弛成功,这便是Dijkstra算法的主要思想:通过 "边" 来松弛 1 号顶点到其余各个顶点的路程。
.- 同理,
通过 2 -> 4 这条边,我们可以将 dis[4] 的值从*(未知)松弛为4.
我们已经知道了 根据一个顶点的所有出边的松弛方法,好么其它的所有顶点的出边松弛都不在话下,最终我们求得 顶点1 到所有顶点的最短路径为:
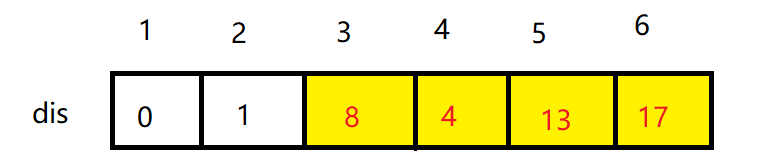
注意的是,我们对一个顶点的所有出边松弛过后,对个顶点进行标记,以防止重复松弛操作 . . .
下面我们来用代码来演示一下这个算法是如何实现的吧 . . .
完整代码如下所示:
#include <stdio.h>
int main()
{
int inf = 9999999; // 表示 * 求知
int i, j, k;
int dis[7], book[7] = { 0 }; // book数组用于标记 当前的顶点的所有出现是否被松弛过
// 第一行、第一列为0,从1开始索引 便于阅读
int e[7][7] = // 邻接矩阵,初始最短路径
{
0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 12,inf,inf,inf,
0,inf, 0, 9, 3,inf,inf,
0,inf,inf, 0,inf, 5,inf,
0,inf,inf, 4, 0, 13, 15,
0,inf,inf,inf,inf, 0, 4,
0,inf,inf,inf,inf,inf, 0
};
for(i = 1; i <= 6; i++) // 顶点1 到其它顶点的初始距离
dis[i] = e[1][i];
book[1] = 1; // 本身顶点1 初始标记
// Dijkstra 算法
for(i = 1; i <= 5; i++) // 应该本身不需要,所以此处为 5次循环
{
int min = inf; // 用于寻找离 1号顶点最近的顶点 (判断距离)
int u = 0; // 用于标记离 1号顶点最近的顶点
for(j = 1; j <= 6; j++)
{
if(book[j] == 0 && dis[j] < min) // 当前的顶点没有匹配过
{
min = dis[j];
u = j;
}
}
book[u] = 1; // 标记查找到的顶点(下次不再查找相同的顶点)
for(k = 1; k <= 6; k++)
{
if(e[u][k] < inf) // 限制范围
{
if(dis[k] > dis[u] + e[u][k])
dis[k] = dis[u] + e[u][k];
}
}
}
for (i = 1; i <= 6; i++)
printf("%d ", dis[i]);
return 0;
}输出结果如上图一样:
0 1 8 4 13 17.
浑浑噩噩,不知所然也 . . .
