线段树

概念
- 线段树就是在二叉树的基础上,每个节点存储一个区间中所有数的和。
- 如果一个节点对应的区间是 \([l, r]\),那么把 \([l, r]\) 分成\(\left [l,\left \lfloor \frac{l+r}{2} \right \rfloor\right ]\)(左儿子)和 \(\left [ \left \lfloor \frac{l+r}{2} \right \rfloor +1,r \right ]\)(右儿子). 根节点表示的区间是[1, n],这样区间 [1, n] 就被划分为一个树形结构.
- 需要注意的还有线段树数组的大小：
  - 线段树的深度是 \(\left \lceil logn \right \rceil\).
  - 线段树是一棵完全二叉树,总节点个数为 \(2 ^ {\left \lceil logn \right \rceil + 1} - 1 < 4n\).
    因此我们至少要把线段树的节点数开成 \(4n\).

建树

根据二叉树的性质，rt的左儿子是rt×2，右儿子是rt×2+1，用位运算可以优化时间效率

code

void build(int rt, int l, int r) {
    if (l == r) { t[rt] = a[l]; return; }//叶子节点，递归边界
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);//递归建立左子树
    build(rt << 1 | 1, mid + 1, r);//递归建立右子树
    t[rt] = t[rt<<1] + t[rt<<1|1];
}

单点查询

修改线段树上的一个节点最多只会影响该节点到根的路径上的这些节点,也就是最多只需要修改\(\left \lfloor logn \right \rfloor\)个节点。

code

void change(int rt, int l, int r) {
    if (l == r) {r[rt] += y; return; }//叶子节点，递归边界
    int mid = (l + r) >> 1;
    if (x <= mid) change(rt << 1, l, mid);
    //x <= mid 说明要修改的数字在左子树
    else change(rt << 1 | 1, mid + 1, r);
    //x <= mid 说明要修改的数字在右子树
    t[rt] = t[rt>>1] + t[rt>>1|1];
}

区间查询

code

int sum(int rt, int l, int r) {
    if (x <= l && r <= y) return t[rt];
    //区间[x, y]完全覆盖线段树[l, r]
    int mid = (l + r) >> 1, ans = 0;
    if (x <= mid) ans += sum(rt << 1, l, mid);
    //区间[x, y]与左儿子[l, mid]有交
    if (y > mid) ans += sum(rt << 1 | 1, mid + 1, r);
    //区间[x, y]与右儿子[mid + 1, r]有交
    return ans;
}

懒惰标记
- 思考：如果对一个区间的每一个数进行修改，复杂度是\(O(nlogn)\),有没有更优的解法？
- 修改和查询一样,可以将其拆成若干个极大的区间,分别修改这些区间，那就要用到今天的重点——懒惰标记
- 我们来进行演示一下
开始的时候

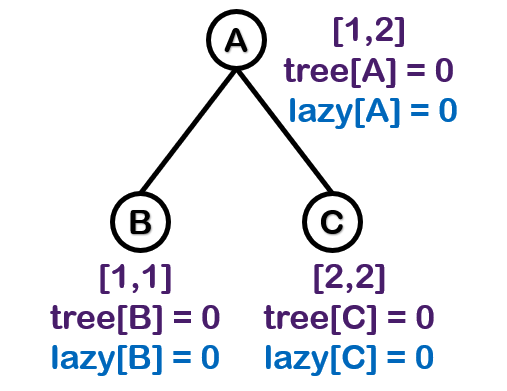
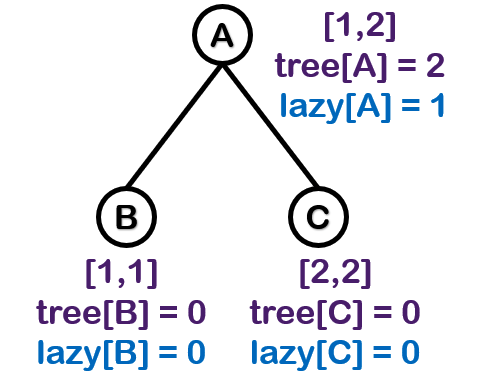
区间修改 [1, 2]
- A 的懒惰标记加 1.
  A 的权值加上 1 ∗ 2(加上的数字 × 区间长度).

区间查询 [1, 2]
- 询问 [1, 2],直接返回 tree[A].

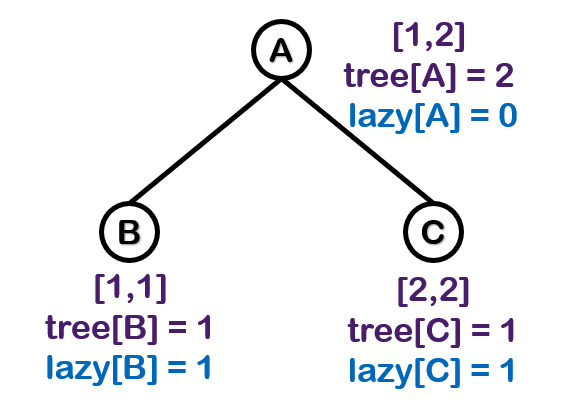
区间查询 [1, 1]
- A 的懒惰标记下传 (特别注意, A 的懒惰标记和 A 无关, A 的懒惰标记是要加在儿子身上的,而不是自己身上)
  tree[B], tree[C] 加上 lazy[A] ∗ 1(懒惰标记 × 区间长度)
  lazy[B], lazy[C] 加上 lazy[A]

区间查询 [2, 2]
- 直接返回 tree[C].

区间修改

updata

void updata(int rt, int l, int r, int w) {
    t[rt] += (r - l + 1) * w;//更新权值
    lazy[rt] += w;//更新懒惰标记
}

pushdown

void pushdown(int rt, int l, int r) {
    int mid = (l + r) >> 1;
    updata(rt << 1, l, mid, lazy[rt]);
    //将懒惰标记下传给左儿子
    updata(rt << 1 | 1, mid + 1, r, lazy[rt]);
    //将懒惰标记下传给右儿子
    lazy[rt] = 0;//懒惰标记清零
}

类似之前的询问操作,修改操作也是将区间拆成 \(logn\) 个区间分别修改,时间复杂度 \(O(logn)\).

code

void change(int rt, int l, int r) {
    if (x <= l && r <= y) {
        updata(rt, l, r, w);
        return;
    }//区间[x, y]完全覆盖线段树[l, r]
    pushdown(rt, l, r);//下传懒惰标记
    int mid = (l + r) >> 1;
    if (x <= mid) change(rt << 1, l, mid);
    //区间[x, y]与左儿子[l, mid]有交
    if (y > mid) change(rt << 1 | 1, mid + 1, r);
    //区间[x, y]与右儿子[mid + 1, r]有交
    t[rt] = t[rt<<1] + t[rt<<1|1];
}

区间查询

有懒惰标记相比没有懒惰标记的时候,区间查询唯一的不同就是需要下放标记.

code

int sum(int rt, int l, int r) {
    if (x <= l && r <= y) return t[rt];
    int mid = (l + r) >> 1, ans = 0;
    pushdown(rt, l, r);//只有这里不一样
    if (x <= mid) ans += sum(rt << 1, l, mid);
    if (y > mid) ans += sum(rt << 1 | 1, mid + 1, r);
    return ans;
}

例题

线段树模板题

code

#include <cstdio>
#define int long long 
/*
#define self rt, l, r
#define lson rt << 1, l, mid
#define rson rt << 1 | 1, mid + 1, r
*/
//这些宏定义可以让代码更简洁
using namespace std;
const int N = 1e5 + 5;
int n, m, a[N], t[N<<2], x, y, w, lazy[N<<2];
void build(int rt, int l, int r) {
    if (l == r) { t[rt] = a[l]; return; }
    int mid = (l + r) >> 1;
    build(rt << 1, l, mid);
    build(rt << 1 | 1, mid + 1, r);
    t[rt] = t[rt<<1] + t[rt<<1|1];
}
void updata(int rt, int l, int r, int w) {
    t[rt] += (r - l + 1) * w;
    lazy[rt] += w;
}
void pushdown(int rt, int l, int r) {
    int mid = (l + r) >> 1;
    updata(rt << 1, l, mid, lazy[rt]);
    updata(rt << 1 | 1, mid + 1, r, lazy[rt]);
    lazy[rt] = 0;
}
void add(int rt, int l, int r) {
    if (x <= l && r <= y) {
        updata(rt, l, r, w);
        return;
    }
    pushdown(rt, l, r);
    int mid = (l + r) >> 1;
    if (x <= mid) add(rt << 1, l, mid);
    if (y > mid) add(rt << 1 | 1, mid + 1, r);
    t[rt] = t[rt<<1] + t[rt<<1|1];
}
int sum(int rt, int l, int r) {
    if (x <= l && r <= y) return t[rt];
    int mid = (l + r) >> 1, ans = 0;
    pushdown(rt, l, r);
    if (x <= mid) ans += sum(rt << 1, l, mid);
    if (y > mid) ans += sum(rt << 1 | 1, mid + 1, r);
    return ans;
}
signed main() {
    scanf("%lld%lld", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    while (m--) {
        int t;
        scanf("%lld%lld%lld", &t, &x, &y);
        if (t == 1) scanf("%lld", &w), add(1, 1, n);
        else printf("%lld\n", sum(1, 1, n));
    }
    return 0;
}

感谢GSL学长的指导

线段树板子（懒惰标记）

线段树

猜你喜欢