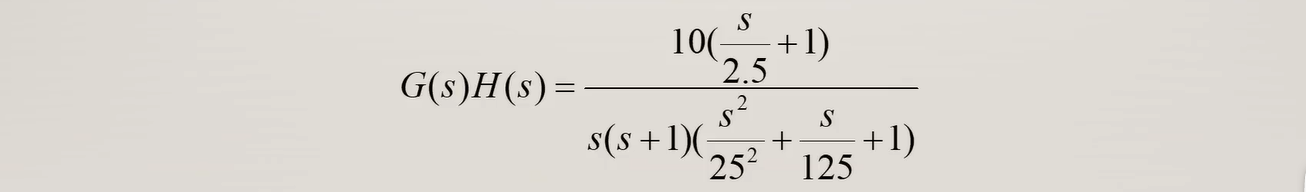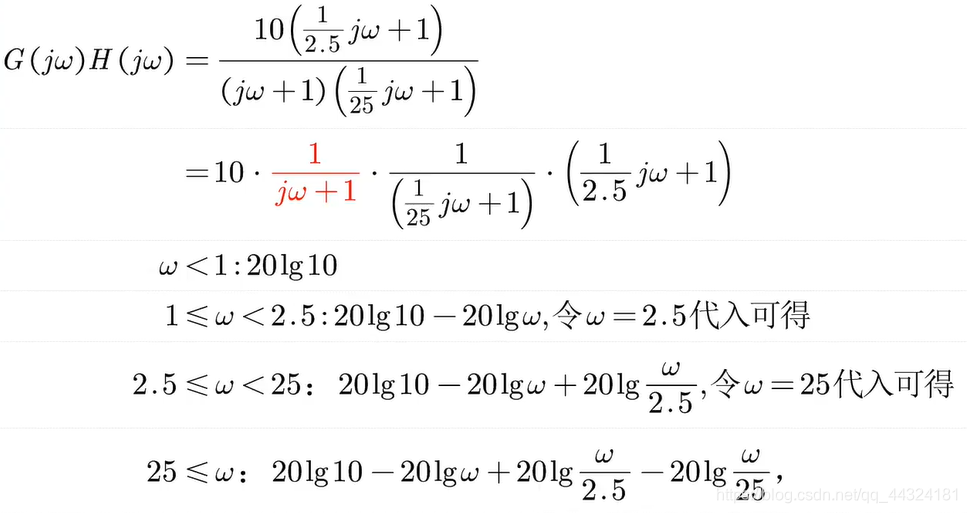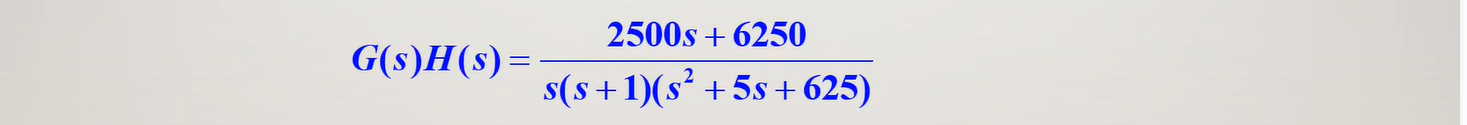B站网课——Bode曲线的绘制

2020-4-21-5.2开环系统Bode曲线绘制

---

1. 叠加法

  由于Bode图中，对数幅频特性绘制的是$20lg|G(j\omega )H(j\omega )|$，而幅值可以化成典型环节幅值的乘积，因此对数幅频特性可以看成是典型环节对数幅频特性的叠加。对数相频特性本身就是叠加关系（环节相乘，相角相加）。
注意：典型环节是尾一多项式形式！
  按转折频率分段进行，斜率是叠加关系。

例5

---

解：

• 开环传递函数典型环节分解形式：
  
• 叠加法Bode图如下：
  

2. 按转折频率（交接频率）分段计算法

2.1 开环对数幅频特性曲线绘制

• 无转折频率的环节：比例、积分、微分
• 有转折频率的环节：一阶惯性、一阶微分、二阶振荡、二阶微分
  • 转折频率之前，是 $0dB$，无需考虑；
  • 转折频率之后，要考虑在内，每遇到一个转折频率，就会多加入一个环节。
• 对数幅频特性曲线的斜率只会随转折频率的出现而发生变化，相邻两个转折频率之间的曲线斜率不变。

---

• 最小的转折频率记为${\omega }_{min}$；
• 在$\omega <{\omega }_{min}$范围内，有转折频率的环节（一阶惯性、一阶微分、二阶振荡、二阶微分）对数幅频特性均为$0dB$，均不用考虑在内，只需要考虑比例、积分和微分，表达式为$\frac{K}{s^{\nu }}$，其对数幅频特性的直线方程为：$$L(\omega )=20lgK-\nu \times lg\omega$$，斜率为$\nu \times (-20dB/dec)$，过$(1,20lgK)$的直线，也会过$(K^{\frac{1}{\nu }},0)$。
• 在$\omega >{\omega }_{min}$范围内，每遇到一个转折频率，就会加上一个典型环节；
• 最终会得出一个分段函数，绘制其曲线即可。

2.2 开环对数相频特性曲线绘制

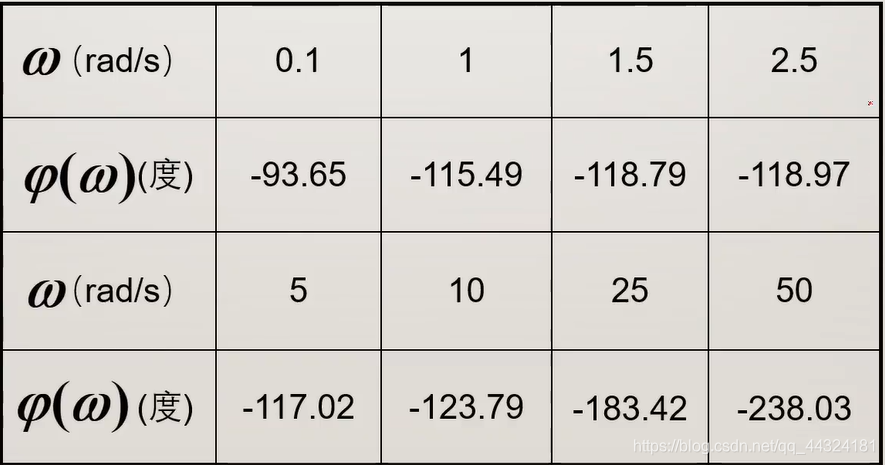
• 把每一个环节的相频特性表达式相加，取不同的 $\omega$ 值，列表、描点、连线即可。

例5

已知系统频率特性如下，试绘制其对数频率特性曲线
$$G(j\omega )=\frac{100(j\omega +2.5)}{(j\omega +1)(j\omega +25)}$$
解：

---

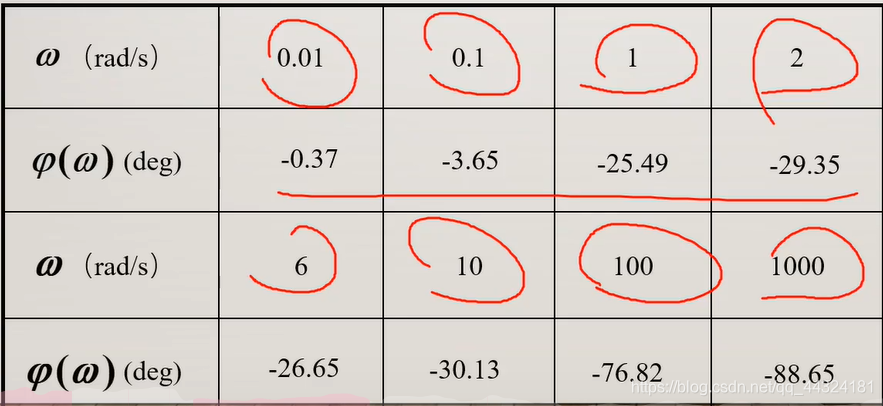
• 取几个点计算：
  
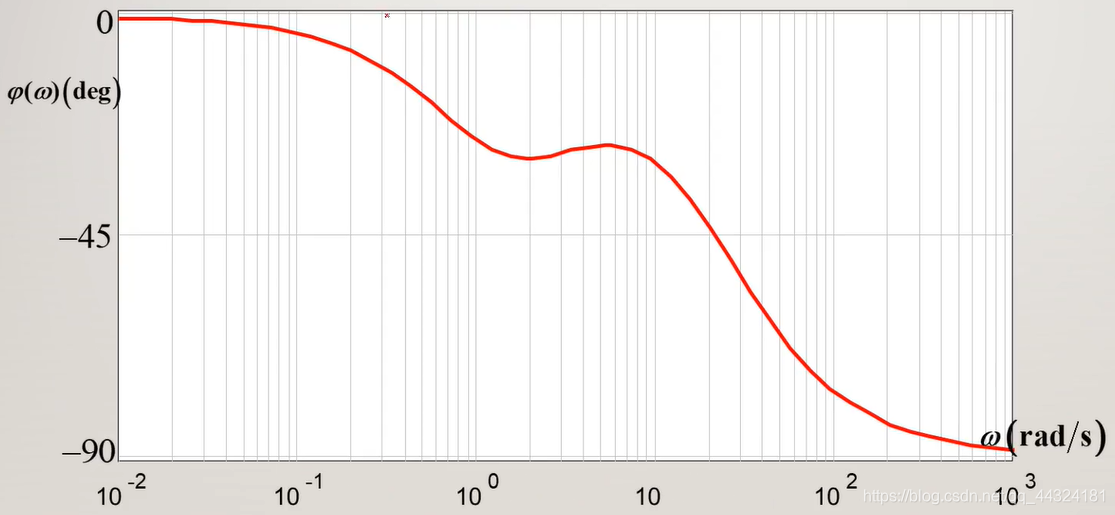
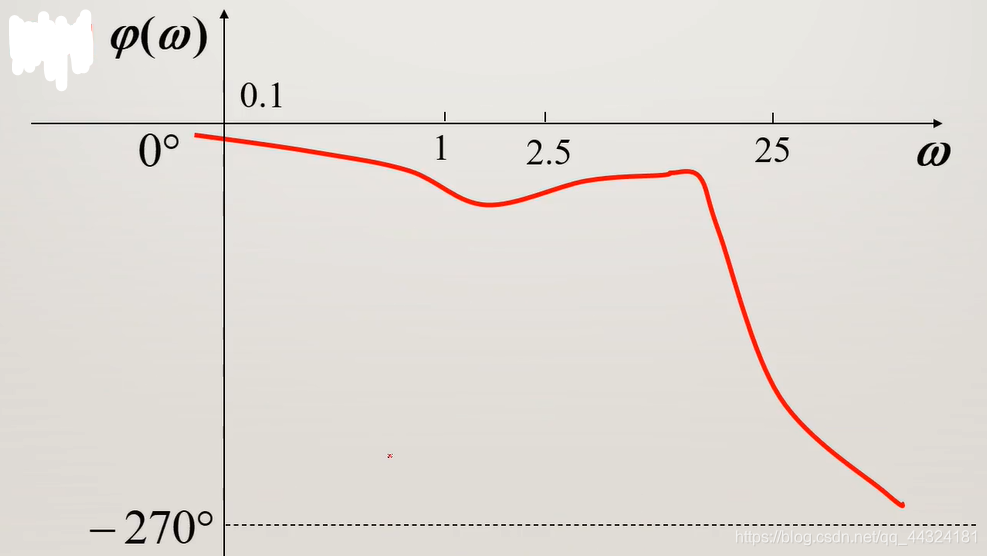
• 描点得：
  

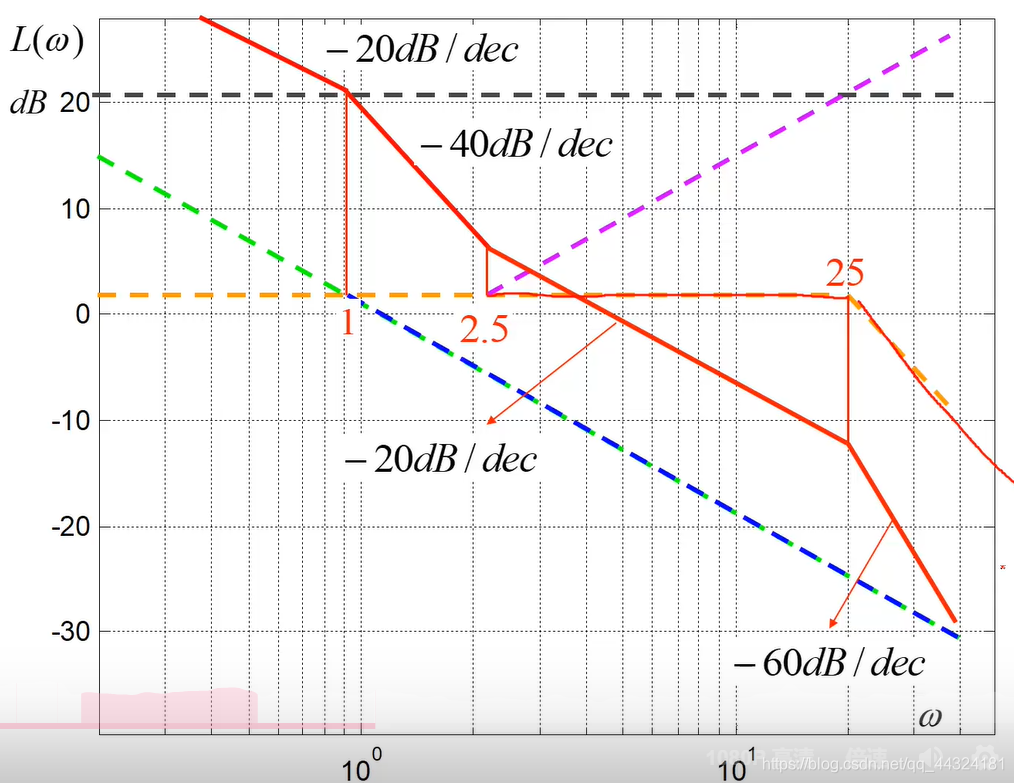
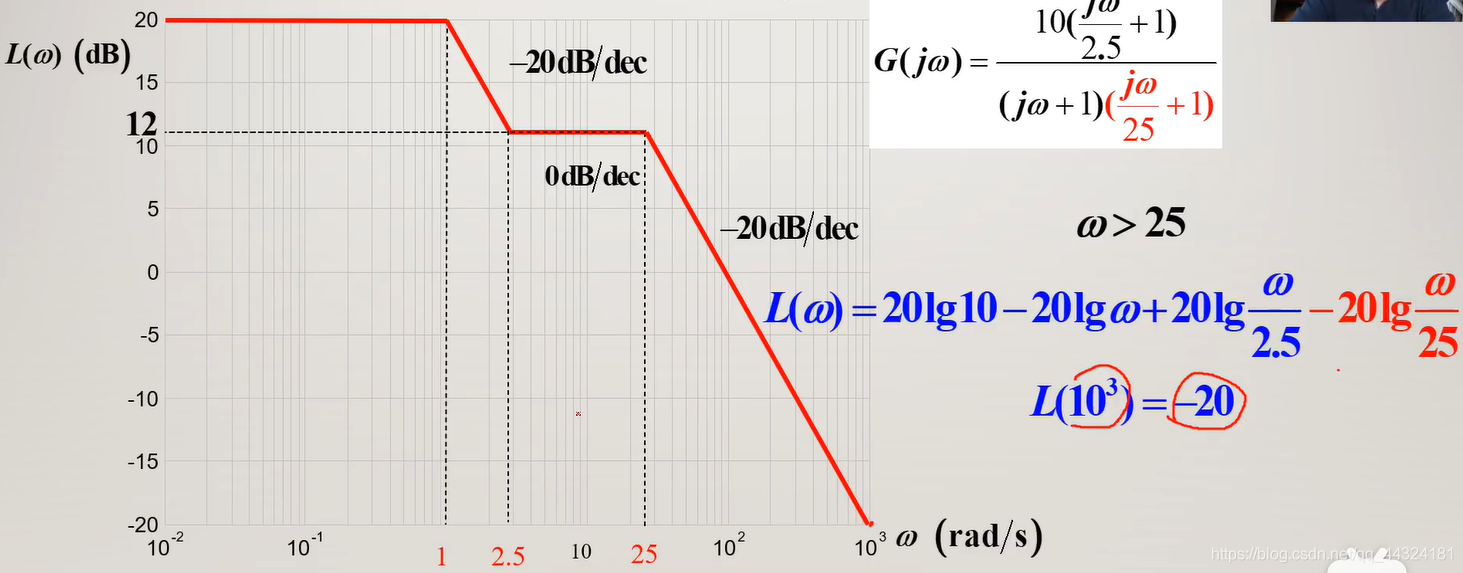
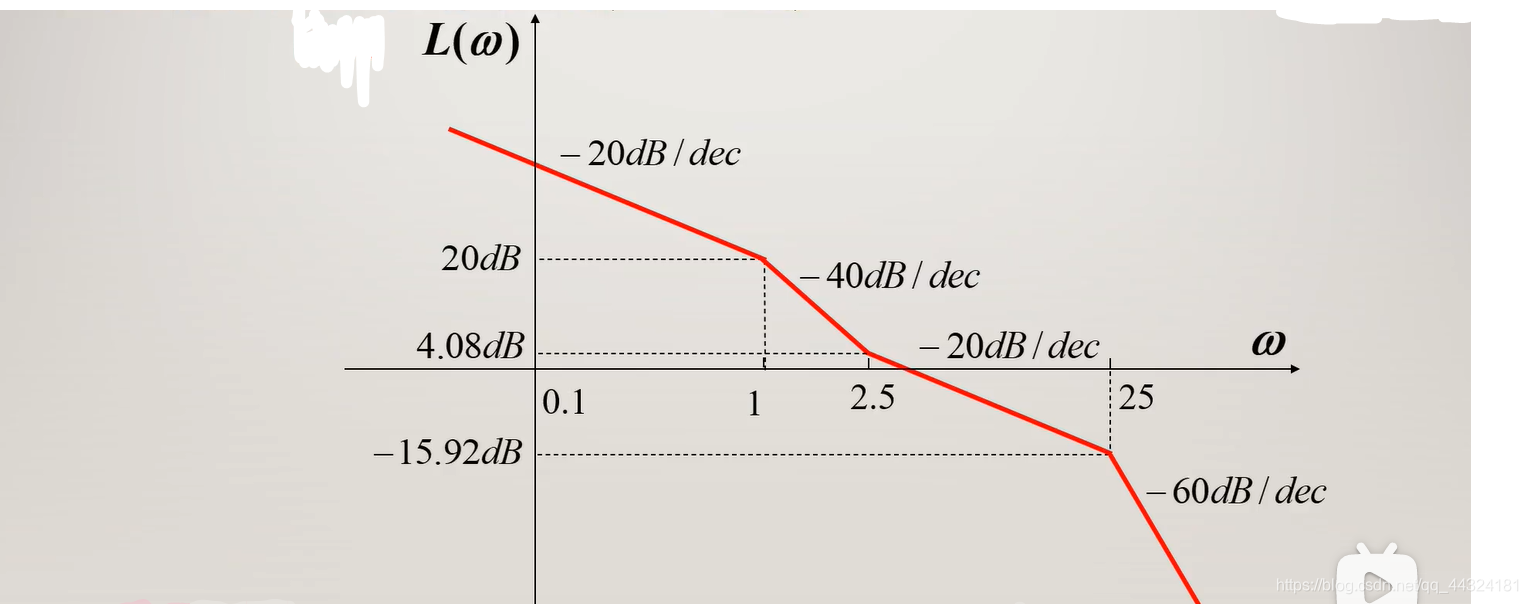
例6

已知系统频率特性如下，试绘制其对数频率特性曲线。

解：

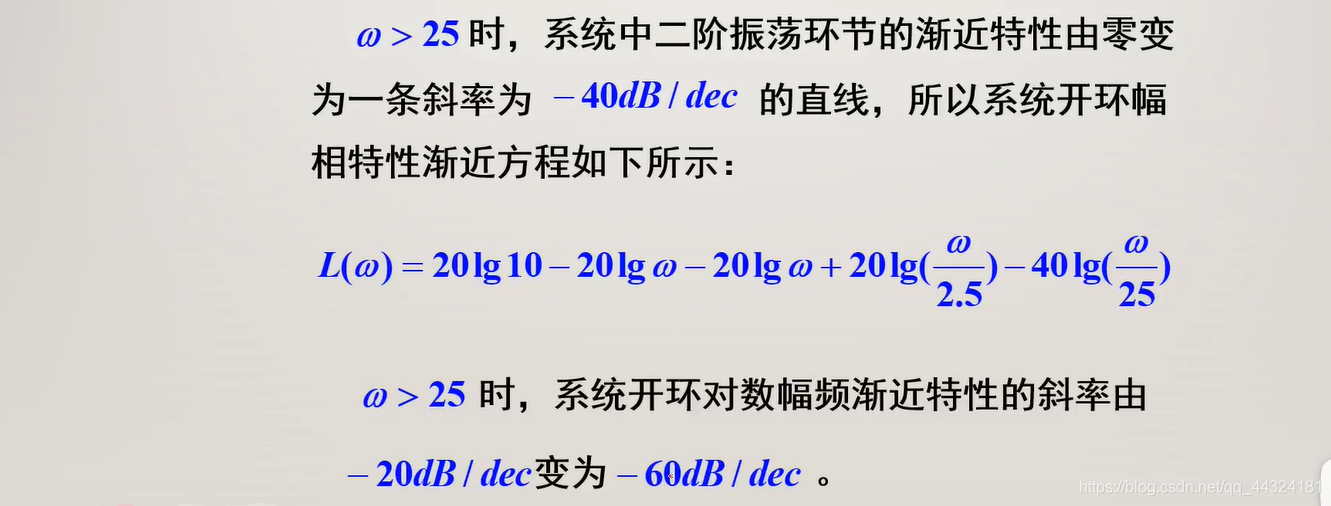
• 绘制系统的开环对数幅频特性曲线
  
  
  
  
  
• 绘制系统的开环对数相频特性曲线
  
  
  

3. Bode图的应用——模型辨识

• 以下是博主自己凝练的几句话：
  • 加不同频率的正弦信号；
  • 绘制处曲线；
  • MATLAB工具箱拟合曲线成折线；
  • 根据频率和幅值求解未知数。

下一篇：奈氏稳定判据