记录一下,方便以后翻阅~
下图是基本的PID算法实现方式,以及实现PID控制器所需的假设和转换。为实现PID控制器,LabVIEW要求算法对输入信号进行采样并离散积分和微分操作。
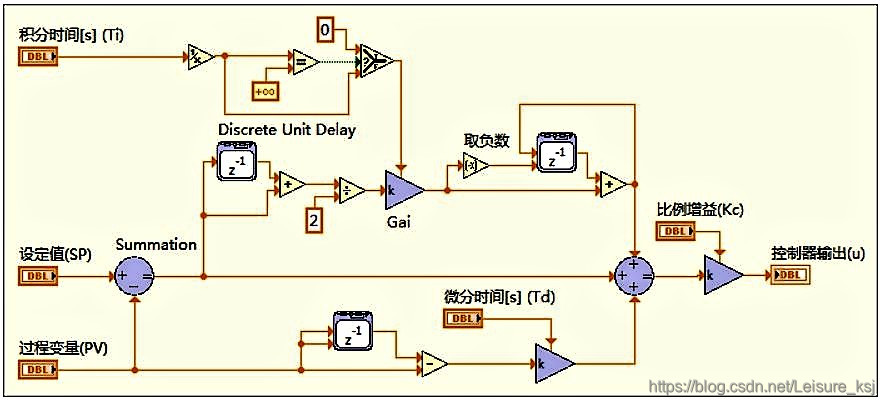
一、误差计算
二、比例操作
三、积分操作(梯形积分)
离散积分操作有几种方式,如前向差分、后向差分和梯形逼近(也称突斯汀或双线性变换)。本PID算法使用梯形积分避免PV或SP的突然改变引起积分操作的剧烈变动,等式如下所示:
四、微分操作
SP的突然变化会引起误差e的微分操作,因而会造成控制器输出振荡。这些振荡被称为微分冲击。为避免微分冲击,可仅向PV应用微分操作,不要向误差e应用微分操作。下列等式表示本PID算法实现的避免微分冲击的微分操作:
五、控制器输出
控制器输出是比例、积分和微分操作的总和,公式如下:
六、输出限制和抗饱和算法
实际控制器输出限制在控制器输出指定的范围内。
如:
七、案例分享
在LabVIEW的Examples库里,有一个名为General PID Simulator.vi文件,前面板大致如下图所示:

程序框图本人进行了简单修改,前面介绍的那些PID公式,其实都封装在了下图红圈的那个VI里:
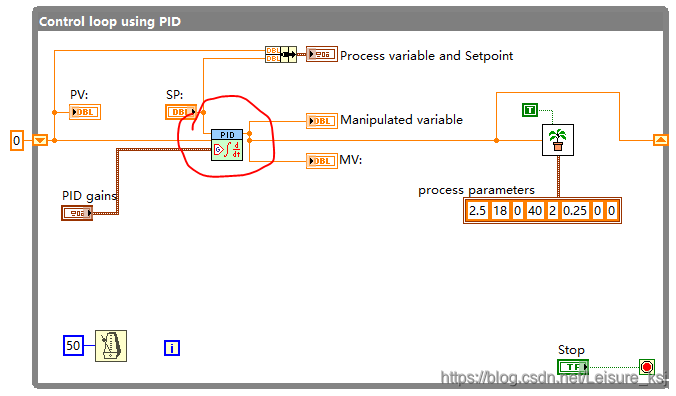
仿真运行时,PV值(过程变量)会不断逼近SP值(设定值),效果如下图所示:
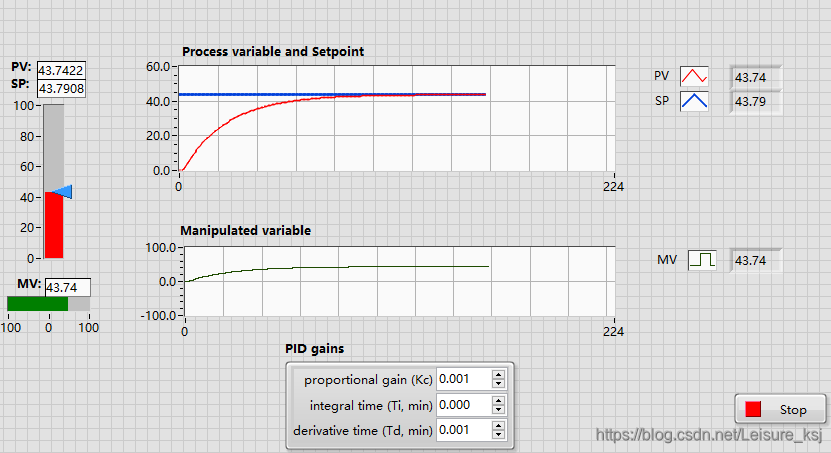
这时,如果改变SP值,那么PV值会朝的新的SP值方向逼近。
八、经验分享
从上面的案例可以发现,当PV值与SP值差值大时,收敛速度很快,并随着PV值与SP值接近而放慢收敛速度。利用这种思想,可以实时追踪一些变化的目标。不过,PID的性能与时间间隔长度有关,ANC(主动降噪)恐怕是不适用了。
