一、简介
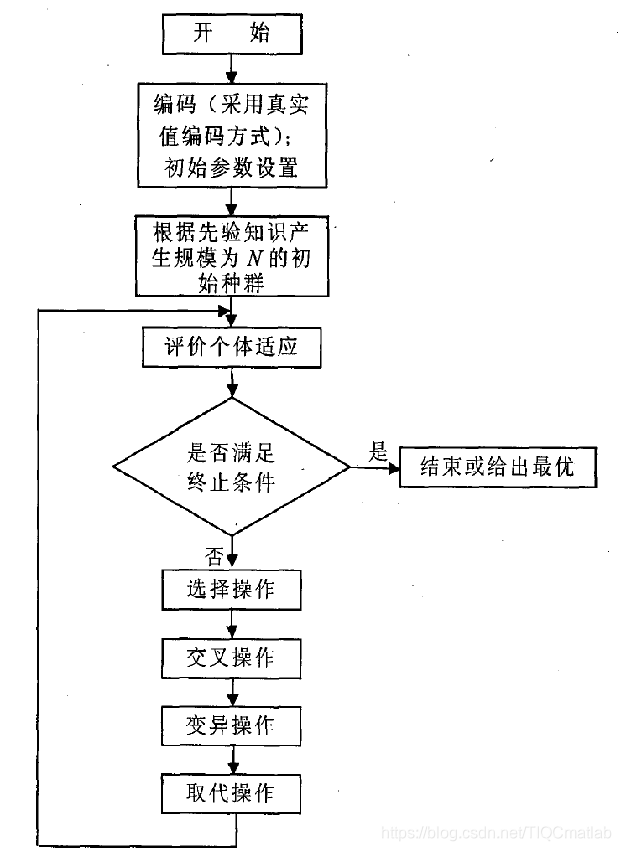
遗传算法的应用步骤
遗传算法GA是基于进化和遗传理论而提出来的全局寻优方法。
简单遗传算法解决问题的基本步骤如下:
(1)初始化:随机生成N个个体作为初始群体P(0),该种群就是目标函数可行解的一个集合。设置进化代数计数器归零,设置最大进化代数iter_max;
(2)个体评价:将初始种群代入目标函数中,根据适应度函数计算当前群体中各个种群的适应度;
(3)终止条件判断:给出终止条件,判断算法是否满足终止条件,若满足则转到(8);
(4)选择运算:对初始群体执行选择操作,优良的个体被大量复制,劣质的个体复制的少甚至被淘汰;
(5)交叉运算:以交叉概率来进行交叉运算;
(6)变异运算:以变异概率来进行交叉运算;
(7)群体P(t)经过选择运算、交叉运算、变异运算之后,得到由N个新个体构成的下一代群体P(t+1),则转(2),否则转(4);
(8)不断的进化,最终会得到目标函数中,适应度最高的个体,将其作为问题的最优解或满意解输出,终止计算。

二、源代码
%%%%遗传算法%%%%
clc;
clear;
close all;
T=[ 46 52 79 45 97 10 44 24 85 75 66 49 95 61 19 47 84 13 11 19 98 2 85 44 7 73 19 69 12 73 85 23 53 16 88 8 26 42 58 63 7 2 44 38 24 76 85 61 32 90
61 87 51 25 73 93 28 90 94 59 64 2 16 35 53 40 81 26 85 4 4 10 63 96 55 71 66 94 7 15 11 99 37 50 56 69 22 56 67 63 96 74 4 42 40 30 93 36 25 87
3 1 58 85 33 71 58 56 64 43 48 69 96 35 82 53 64 11 61 36 53 87 88 10 32 38 25 24 90 7 11 49 2 76 17 32 39 9 83 69 67 28 88 23 91 71 3 26 41 96
51 24 21 57 69 51 50 51 21 19 63 91 11 6 31 63 36 39 57 47 56 65 59 4 10 12 62 43 49 54 87 29 2 18 75 39 77 69 15 78 68 37 22 41 92 67 24 87 91 31
37 16 42 47 94 14 94 34 72 36 88 51 41 71 94 99 11 97 44 77 69 91 38 25 87 7 66 54 86 49 3 48 44 93 37 82 31 59 78 33 36 3 58 10 98 6 44 62 24 94
79 93 68 75 37 44 34 39 76 62 74 28 78 43 98 83 91 27 6 82 60 44 43 76 99 66 11 35 52 8 40 62 25 24 30 1 73 27 16 91 33 11 99 2 60 90 36 62 15 3
83 87 38 38 86 67 23 19 97 78 66 67 7 23 67 8 77 71 85 29 49 3 94 76 95 48 4 37 82 57 61 6 97 5 27 95 46 92 46 52 8 11 7 54 72 57 85 22 87 65
22 29 99 25 98 55 80 82 33 68 47 74 26 61 95 55 11 42 72 14 8 98 90 36 75 69 26 24 55 98 86 30 92 94 66 47 3 41 41 47 89 28 39 80 47 57 74 38 59 5
27 92 75 94 18 41 37 58 56 20 2 39 91 81 33 14 88 22 36 65 79 23 66 5 15 51 2 81 12 40 59 32 16 87 78 41 43 94 1 93 22 93 62 53 30 34 27 30 54 77
24 47 39 66 41 46 24 23 68 50 93 22 64 81 94 97 54 82 11 91 23 32 26 22 12 23 34 87 59 2 38 84 62 10 11 93 57 81 10 40 62 49 90 34 11 81 51 21 39 2];
N=50;%种群大小
PRECI=size(T,1);%个体进制
gmax=100;%最大迭代次数
Ne=50;
trial=1;
paretof=[];
Pc=0.95;
Pm=0.05;
NPOP=ga_InitPop(N,PRECI);
EPOP=[];Epa=[];
it=0;
while it<gmax
twoPOP=[NPOP;EPOP];
[Objv,Total]=ga_caltime(NPOP,T);%compute objective values
Npa=[Objv,Total];
twopa=[Npa;Epa];
[Fit,FASPEA2t]=FASPEA2f(twopa);%fitness assignment
%--------------------------------------------------------------------------
[EPOP,Epa,APESPEA2t]=APESPEA2f(twoPOP,twopa,Fit,Ne);%enviromental selection
%--------------------------------------------------------------------------
[EFit,FASPEA2t2]=FASPEA2f(Epa);
[NPOP,BTSt]=BTSf(EPOP,EFit,N);
NPOP=LoxRecombin(NPOP,Pc);
NPOP=ga_Mutate(NPOP,Pm);
it=it+1;
disp(sprintf('time: %d generation: %d ',trial,it));
end
twoPOP=[NPOP;EPOP];
[Objv,Total]=ga_caltime(NPOP,T);%compute objective values
Npa=[Objv,Total];
twopa=[Npa;Epa];
[Fit,FASPEA2t]=FASPEA2f(twopa);
[er,ec]=size(Epa);
for i=1:er
pp=Epa(i,:);
for j=i+1:er
if pp==Epa(j,:)
Epa(j,:)=zeros(1,ec);
end
end
end
function pa=OVcom(v,NO)
% OVcom: define the test problems,compute the objective values to v
% usage:
% pa=OVcom(v,NO);
% where
% NO: the serial number of test problem
% v: the solutions in decision space
% pa: the solutions in objective space
switch NO
%%1-3 are MISA's problems
case 1 %% MISA's Example 1 %DEB
x=v(:,1);y=v(:,2);
f1=x;
f2=(1+10*y).*(1-(x./(1+10*y)).^2-(x./(1+10*y)).*sin(2*pi*4*x));
pa=[f1,f2];
case 2%% MISA's Example 2 %SCH
x=v;
f1=zeros(size(v,1),1);
f2=(x-5).^2;
sx1=find(x<=1);x1=x(sx1);f1(sx1)=-x1;
sx2=find(x>1&x<=3);x2=x(sx2);f1(sx2)=-2+x2;
sx3=find(x>3&x<=4);x3=x(sx3);f1(sx3)=4-x3;
sx4=find(x>4);x4=x(sx4);f1(sx4)=x4-4;
pa=[f1,f2];
case 3 %% MISA's Example 5 %KUR
x=v(:,1);y=v(:,2);z=v(:,3);
f1=-10*exp(-0.2*sqrt(x.^2+y.^2))-10*exp(-0.2*sqrt(y.^2+z.^2));
f2=((abs(x)).^0.8+5*sin((x).^3))+((abs(y)).^0.8+5*sin((y).^3))+((abs(z)).^0.8+5*sin((z).^3));
pa=[f1,f2];
%%4-18 are Veldhuizen's probems
case 4 %% Binh (1)
x=v(:,1);y=v(:,2);
f1=x.^2+y.^2;
f2=(x-5).^2+(y-5).^2;
pa=[f1,f2];
case 5 %% Binh (3)
x=v(:,1);y=v(:,2);
f1=x-10.^6;
f2=y-2*10.^(-6);
f3=x.*y-2;
pa=[f1,f2,f3];
case 6 %% Fonseca
x=v(:,1);y=v(:,2);
f1=1-exp(-(x-1).^2-(y+1).^2);
f2=1-exp(-(x+1).^2-(y-1).^2);
pa=[f1,f2];
case 7 %% Fonseca (2)
x=v(:,1);y=v(:,2);z=v(:,3);
f1=1-exp(-(x-1/sqrt(3)).^2-(y-1/sqrt(3)).^2-(z-1/sqrt(3)).^2);
f2=1-exp(-(x+1/sqrt(3)).^2-(y+1/sqrt(3)).^2-(z+1/sqrt(3)).^2);
pa=[f1,f2];
case 8 %% Laumanns
x=v(:,1);y=v(:,2);
f1=x.^2+y.^2;
f2=(x+2).^2+y.^2;
pa=[f1,f2];
case 9 %% Lis
x=v(:,1);y=v(:,2);
f1=(x.^2+y.^2).^(1/8);
f2=((x-0.5).^2+(y-0.5).^2).^(1/4);
pa=[f1,f2];
case 10 %% Murata
x=v(:,1);y=v(:,2);
f1=2* sqrt(x);
f2=x.*(1-y)+5;
pa=[f1,f2];
case 11 %% Poloni
x=v(:,1);y=v(:,2);
A1=0.5*sin(1)-2*cos(1)+sin(2)-1.5*cos(2);
A2=1.5*sin(1)-cos(1)+2*sin(2)-0.5*cos(2);
B1=0.5*sin(x)-2*cos(x)+sin(y)-1.5*cos(y);
B2=1.5*sin(x)-cos(x)+2*sin(y)-0.5*cos(y);
f1=(1+(A1-B1).^2+(A2-B2).^2);
f2=((x+3).^2+(y+1).^2);
pa=[f1,f2];
case 12 %% Quagliarella
A1=(v(:,1).^2-10*cos(2*pi*v(:,1))+10)+(v(:,2).^2-10*cos(2*pi*v(:,2))+10)+(v(:,3).^2-10*cos(2*pi*v(:,3))+10);
A2=((v(:,1)-1.5).^2-10*cos(2*pi*(v(:,1)-1.5))+10)+((v(:,2)-1.5).^2-10*cos(2*pi*(v(:,2)-1.5))+10)+((v(:,3)-1.5).^2-10*cos(2*pi*(v(:,3)-1.5))+10);
f1=sqrt(A1/3);
f2=sqrt(A2/3);
pa=[f1,f2];
case 13 %% Rendon
x=v(:,1);y=v(:,2);
f1=1./(x.^2+y.^2+1);
f2=x.^2+3*y.^2+1;
pa=[f1,f2];
case 14 %% Rendon (2)
x=v(:,1);y=v(:,2);
f1=x+y+1;
f2=x.^2+2*y-1;
pa=[f1,f2];
case 15 %% Schaffer
x=v;
f1=x.^2;
f2=(x-2).^2;
pa=[f1,f2];
case 16 %% Viennet
x=v(:,1);y=v(:,2);
f1=x.^2+(y-1).^2;
f2=x.^2+(y+1).^2+1;
f3=(x-1).^2+y.^2+2;
pa=[f1,f2,f3];
case 18 %% Viennet (3)
x=v(:,1);y=v(:,2);
f1=0.5*(x.^2+y.^2)/2+sin(x.^2+y.^2);
f2=(3*x-2*y+4).^2/8+(x-y+1).^2/27+15;
f3=1./(x.^2+y.^2+1)-1.1*exp(-x.^2-y.^2);
pa=[f1,f2,f3];
%DTLZ
case 19 %%DTLZ1
vg=v(:,3:5);
gx=100*(3+sum((vg-0.5).^2-cos(20*pi*(vg-0.5)),2));
f1=0.5*v(:,1).*v(:,2).*(1+gx);
f2=0.5*v(:,1).*(1-v(:,2)).*(1+gx);
f3=0.5*(1-v(:,1)).*(1+gx);
pa=[f1,f2,f3];
case 20 %%DTLZ2
vg=v(:,3:12);
gx=sum((vg-0.5).^2,2);
f1=(1+gx).*cos(v(:,1)*0.5*pi).*cos(v(:,2)*0.5*pi);
f2=(1+gx).*cos(v(:,1)*0.5*pi).*sin(v(:,2)*0.5*pi);
f3=(1+gx).*sin(v(:,1)*0.5*pi);
pa=[f1,f2,f3];
case 21%%DTLZ3
vg=v(:,3:12);
gx=100*(10+sum((vg-0.5).^2-cos(20*pi*(vg-0.5)),2));
f1=(1+gx).*cos(v(:,1)*0.5*pi).*cos(v(:,2)*0.5*pi);
f2=(1+gx).*cos(v(:,1)*0.5*pi).*sin(v(:,2)*0.5*pi);
f3=(1+gx).*sin(v(:,1)*0.5*pi);
pa=[f1,f2,f3];
case 22%%DTLZ4
vg=v(:,3:12);
gx=sum((vg-0.5).^2,2);
f1=(1+gx).*cos((v(:,1).^100)*0.5*pi).*cos((v(:,2).^100)*0.5*pi);
f2=(1+gx).*cos((v(:,1).^100)*0.5*pi).*sin((v(:,2).^100)*0.5*pi);
f3=(1+gx).*sin((v(:,1).^100)*0.5*pi);
pa=[f1,f2,f3];
% case 23%DTLZ5
% vg=v(:,3:12);
% gx=sum((vg-0.5).^2,2);
% Q1=(1./(2*(1+gx))).*(1+2*gx.*v(:,1));
% Q2=(1./(2*(1+gx))).*(1+2*gx.*v(:,2));
% f1=(1+gx).*cos(Q1*0.5*pi).*cos(Q2*0.5*pi);
% f2=(1+gx).*cos(Q1*0.5*pi).*sin(Q2*0.5*pi);
% f3=(1+gx).*sin(Q1*0.5*pi);
% pa=[f1,f2,f3];
三、运行结果
四、备注
完整代码或者代写添加QQ 912100926
往期回顾>>>>>>
【车间调度】粒子群优化算法之车间调度【Matlab 001期】
【车间调度】遗传算法之基于GUI的车间调度模型【Matlab 002期】
【车间调度】遗传算法之求解车间调度【Matlab 003期】
【车间调度】nsgaII算法之求解车间调度【Matlab 004期】
【车间调度】改进蛙跳算法之求解车间调度问题【Matlab 071期】
【车间调度】置换流水车间调度【Matalb 210期】
【车间调度】PSO求解6X6的车间调度问题【Matlab 305期】
【车间调度】粒子群的生产调度【Matlab 306期】
