网上一搜全是公式,公式很好懂,然后直接贴代码,简直都是一个模子刻的题解。
当然确实代码很简单,能看懂,但没有图我自己要画半天啊??
洛谷3865【模板】ST表
如果不知道公式以及边界条件判断可以参考这篇题解。或者这篇英文讲解
简单介绍下公式:
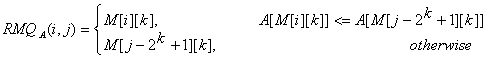
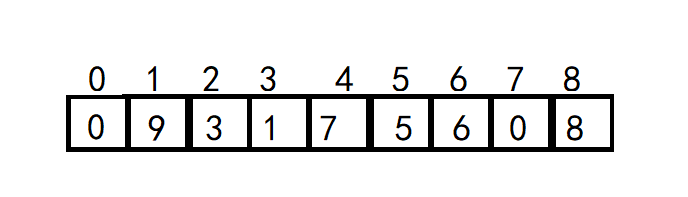
我先给出洛谷样例数组方便观察:9 3 1 7 5 6 0 8
(注意我们数组从1开始存)好像画的有点丑 o( ̄ε ̄*)
我们用数组M[i][j]表示以i为起点,区间长度为2^j的区间最值。比如M[2][2]就是从第2个数开始长度为为4的最大值,3,1,7,5中显然7为最大值,所以M[2][2]=7。
那么对M[i][j]一个第i个数为起点,i+2j-1为终点的连续2^j个数里面最大的,而这个区间可以分为两个相等小区间 ,每份长度均为2^(j - 1)。即[i, i+2j-1 -1] 和 [i+2j-1, i+2j-1]这两个区间。
借一下上面链接大佬的图:把下面蓝色长度划分为红绿两个子区间。

比如M[1][1]是从角标1开始的4个数中最大值,可以理解为从1开始的2个数最大值与从3开始的2个数中最大值的最大值。
那么显然M[i][0]=a[i],从i个数长度为1的区间就是最大值就是自己本身啊。
初始化M[i][j]
for (int i = 1; i <= n; i++) f[i][0] = a[i];
得到的数据是这样的:注意角标从1开始所以第0行为0;
0 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
然后开始算第一列,什么意思呢,M[i][1]表示从第i个数字长度为2的最大值。
对于样例 9 3 1 7 5 6 0 8来说,M[1][[1]是9-3的最大值,为3,M[2][1]是3-1的最大值,是1,1-7的最大值为7……

然后M数组变成(第0行不画了)
9 9 0 0 0 0 0 0 0
3 3 0 0 0 0 0 0 0
1 7 0 0 0 0 0 0 0
7 7 0 0 0 0 0 0 0
5 6 0 0 0 0 0 0 0
6 6 0 0 0 0 0 0 0
0 8 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
依次类推,当j=2时可以从j=1来过渡出最大值,这样比如M[1][2]就是9和7中最大的9(M[1][1]与M[3][1]中最大的)

M数组变成
9 9 9 0 0 0 0 0 0
3 3 7 0 0 0 0 0 0
1 7 7 0 0 0 0 0 0
7 7 7 0 0 0 0 0 0
5 6 8 0 0 0 0 0 0
6 6 0 0 0 0 0 0 0
0 8 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
最后一步类似,i=1,j=3时2^3=8已经到了n了就结束dp;
M数组:M[1][3]=max(9,8)=9;
9 9 9 9 0 0 0 0 0
3 3 7 0 0 0 0 0 0
1 7 7 0 0 0 0 0 0
7 7 7 0 0 0 0 0 0
5 6 8 0 0 0 0 0 0
6 6 0 0 0 0 0 0 0
0 8 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
现在懂了吧,画个图就能解决的事非要我百度半天看公式。 哪个白学家还不会st表拖出去打死。
当然上面是怎么求M数组,求区间的话看下上面发的链接很好懂的。即从左边和右边查最大值覆盖所查区间即可。
附上洛谷ac代码
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 5;
int n, m;
int a[maxn];
int M[maxn][20];
inline int read()
{
int x = 0, f = 1; char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) {
x = x * 10 + ch - 48; ch = getchar(); }
return x * f;
}
void st() {
int lc = log2(n);
for (int i = 1; i <= n; i++)M[i][0] = a[i];
for (int i = 1; i <= lc; i++) {
for (int j = 1; j + (1<<i)- 1<=n; j++) {
M[j][i] = max(M[j][i-1],M[j+(1<<i-1)][i-1]);
}
}
}
int query(int l,int r) {
int k = log2(r - l + 1);
return max(M[l][k], M[r- (1 << k)+1][k]);
}
int main() {
n = read();
m = read();
for (int i = 1; i <= n; i++) a[i] = read();
st();
while (m--)
{
int l, r, ans;
l = read();
r = read();
ans = query(l, r);
printf("%d\n", ans);//行末多打换行洛谷好像可以过
}
return 0;
}