2. 解救小哈
任务:
迷宫由n行m列的单元格组成(n和m都小于等于50),每个单元格要么是空地,要么是障碍物。
任务是帮助小哼找到一条从迷宫的起点通往小哈所在位置的最短路径。注意障碍物是不能走的,当然小哼也不能走到迷宫之外。
解答:
首先可以用一个二维数组来存储这个迷宫。
只能一个一个地去尝试。可以先让小哼往右边走,直到走不通的时候再回到这里,再去试另外一个方向。
这里规定一个顺序,按照顺时针的方向来尝试(即按照右、下、左、上的顺序去尝试)。
例如下图就是一种可行的搜索路径:
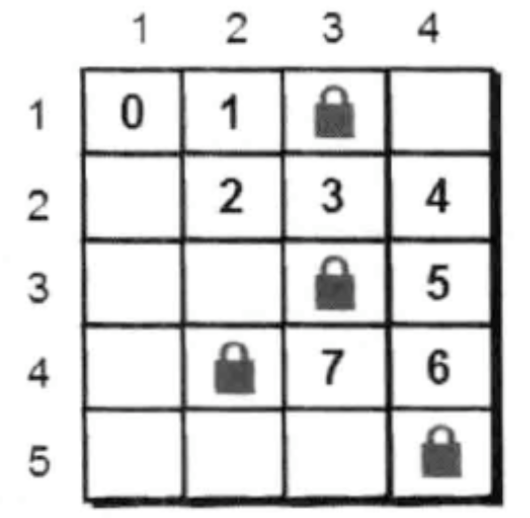
现在尝试用深度优先搜索来实现这个方法。
先来看dfs() 函数如何写。dfs() 函数的功能是解决当前应该怎么办。而小哼处在某个点的时候需要处理的是:先检查小哼是否已经到
达小哈的位置,如果没有到达则找出下一步可以走的地方。
为了解决这个问题, 此处dfs()函数只需要维护3个参数,分别是当前这个点的x坐标、y坐标以及当前已经走过的步数step。
dfs() 函数定义如下:
void dfs(int x, int y, int step) {
return 0;
}
判断是否已经到达小哈的位置,只需要判断当前的坐标和小哈的坐标是否相等就可以了,如果相等则表明已经到达小哈的位置,如下:
void dfs(int x, int y, int step) {
//判断是否到达小哈的位置
if (x==p && y==q) {
//更新最小值
if (step < min) {
min = step;
}
return;//注意返回
}
return 0;
}
如果没有到达小哈的位置,则找出下一步可以走的地方。
因为有四个方向可以走,根据之前的约定,按照顺时针的方向来尝试(即按照右、下、左、上的顺序尝试)。
这里定义了一个方向数组next,如下:
int next[4][2] = {
{
0, 1},//向右走
{
1, 0},//向下走
{
0, -1},//向左走
{
-1, 0}};//向上走
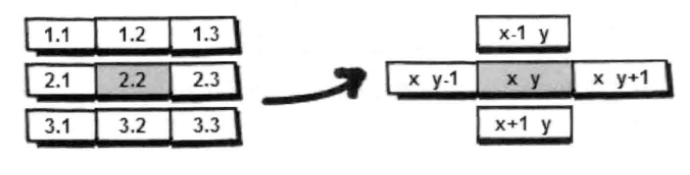
通过这个方向数组,使用循环就很容易获得下一步的坐标。
这里将下一步的横坐标用tx存储,纵坐标用ty存储:
for (k=0; k<=3; k++) {
tx = x+next[k][0];
ty = y+next[k][1];
}
接下来就要对下一个点(tx,ty)进行一些判断。包括是否越界,是否为障碍物,以及这个点是否已经在路径中(即避免重复访问一个点)。
需要用book[tx][ty] 来记录格子(tx, ty)是否已经在路径中。
如果这个点符合所有的要求,就对这个点进行下一步的扩展,即dfs(tx, ty, step+1):
for (k=0; k<=3; k++) {
tx = x + next[k][x];
ty = y + next[k][y];
if (tx<1 || tx>n || ty<1 || ty>m) {
if (a[tx][ty]==0 && book[tx][ty]==0) {
book[tx][ty] = 1;
dfs(tx,ty,step+1);
book[tx][ty] = 0;
}
}
}
完整代码如下:
#include <stdio.h>
int n, m, p, q, min=99999999;
int a[51][51], book[51][51];
void dfs(int x, int y, int step) {
int next[4][2] = {
{
0,1}, //向右走
{
1,0},//向下走
{
0,-1}, //向左走
{
-1,0}};//向上走
int tx, ty, k;
//判断是否到达小哈的位置
if (x==p && y==q) {
//更新最小值
if (step<min) {
min = step;
}
return;//注意返回
}
//枚举4种走法
for (k=0; k<=3; k++) {
//计算下一个点的坐标
tx = x + next[k][0];
ty = y + next[k][1];
//判断是否越界
if (tx<1 || tx>n || ty<1 || ty>n) {
continue;
}
//判断该点是否为障碍物或已经在路径中
if (a[tx][ty]==0 && book[tx][ty]==0) {
book[tx][ty] = 1;//标记这个点已经走过
dfs(tx, ty, step+1);//开始尝试下一个点
book[tx][ty] = 0;//尝试结束,取消这个点的标记
}
}
return;
}
int main() {
int i, j, startx, starty;
//读入n和m,n为行,m为列
scanf("%d %d", &n, &m);
//读入迷宫
for (i=1; i<=n; i++) {
for (j=1; j<=m; j++) {
scanf("%d", &a[i][j]);
}
}
//读入起点和终点坐标
scanf("%d %d %d %d", &startx, &starty, &p, &q);
//从起点开始搜索
book[startx][starty] = 1;//标记起点已经在路径中,方式后面重复走
//第一个参数是起点的x坐标,第二个参数是起点的y坐标,第三个参数是初始步数0
dfs(startx, starty, 0);
//输出最短步数
printf("%d", min);
getchar();getchar();
return 0;
}
数据验证:
第一行有两个数 n m。n 表示迷宫的行,m 表示迷宫的列。
n 行 m 列为迷宫,0表示空地,1表示障碍物。
最后一行4个数,前两个数为迷宫入口的x和y坐标。后两个为小哈的x和y坐标。
5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
返回值:
7
参考
《啊哈!算法》 —— 第4章 万能的搜索