《MATLAB 神经网络43个案例分析》：第16章 基于SVM的回归预测分析——上证指数开盘指数预测

企业开发 2022-06-15 13:14:27 阅读次数: 0

《MATLAB 神经网络43个案例分析》：第16章 基于SVM的回归预测分析——上证指数开盘指数预测

1. 前言

《MATLAB 神经网络43个案例分析》是MATLAB技术论坛（www.matlabsky.com）策划，由王小川老师主导，2013年北京航空航天大学出版社出版的关于MATLAB为工具的一本MATLAB实例教学书籍，是在《MATLAB神经网络30个案例分析》的基础上修改、补充而成的，秉承着“理论讲解—案例分析—应用扩展”这一特色，帮助读者更加直观、生动地学习神经网络。

《MATLAB神经网络43个案例分析》共有43章，内容涵盖常见的神经网络（BP、RBF、SOM、Hopfield、Elman、LVQ、Kohonen、GRNN、NARX等）以及相关智能算法（SVM、决策树、随机森林、极限学习机等）。同时，部分章节也涉及了常见的优化算法（遗传算法、蚁群算法等）与神经网络的结合问题。此外，《MATLAB神经网络43个案例分析》还介绍了MATLAB R2012b中神经网络工具箱的新增功能与特性，如神经网络并行计算、定制神经网络、神经网络高效编程等。

近年来随着人工智能研究的兴起，神经网络这个相关方向也迎来了又一阵研究热潮，由于其在信号处理领域中的不俗表现，神经网络方法也在不断深入应用到语音和图像方向的各种应用当中，本文结合书中案例，对其进行仿真实现，也算是进行一次重新学习，希望可以温故知新，加强并提升自己对神经网络这一方法在各领域中应用的理解与实践。自己正好在多抓鱼上入手了这本书，下面开始进行仿真示例，主要以介绍各章节中源码应用示例为主，本文主要基于MATLAB2015b(32位)平台仿真实现，这是本书第十六章基于SVM的回归预测分析实例，话不多说，开始！

2. MATLAB 仿真示例

打开MATLAB，点击“主页”，点击“打开”，找到示例文件
在这里插入图片描述

选中chapter_sh.m，点击“打开”，chapter_sh.m源码如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能：基于SVM的回归预测分析——上证指数开盘指数预测
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-06-14
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% Matlab神经网络43个案例分析

% 基于SVM的回归预测分析——上证指数开盘指数预测
% by 李洋(faruto)
% http://www.matlabsky.com
% Email:faruto@163.com
% http://weibo.com/faruto 
% http://blog.sina.com.cn/faruto
% 2013.01.01
%% 清空环境变量
function chapter_sh
tic;
close all;
clear;
clc;
format compact;
%% 数据的提取和预处理
tic
% 载入测试数据上证指数(1990.12.19-2009.08.19)
% 数据是一个4579*6的double型的矩阵,每一行表示每一天的上证指数
% 6列分别表示当天上证指数的开盘指数,指数最高值,指数最低值,收盘指数,当日交易量,当日交易额.
load chapter_sh.mat;

% 提取数据
[m,n] = size(sh);
ts = sh(2:m,1);
tsx = sh(1:m-1,:);

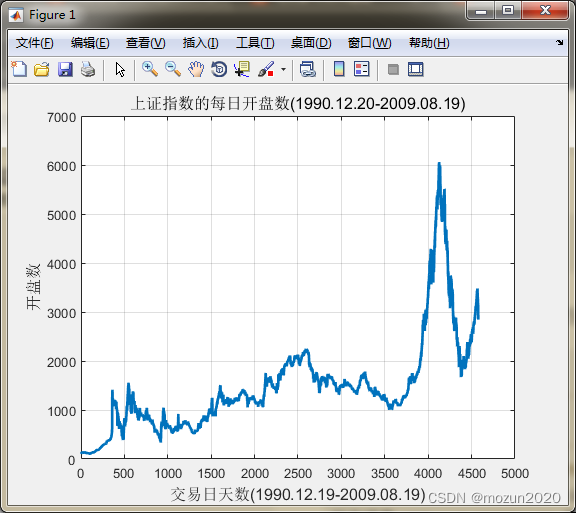
% 画出原始上证指数的每日开盘数
figure;
plot(ts,'LineWidth',2);
title('上证指数的每日开盘数(1990.12.20-2009.08.19)','FontSize',12);
xlabel('交易日天数(1990.12.19-2009.08.19)','FontSize',12);
ylabel('开盘数','FontSize',12);
grid on;

% 数据预处理,将原始数据进行归一化
ts = ts';
tsx = tsx';

% mapminmax为matlab自带的映射函数	
% 对ts进行归一化
[TS,TSps] = mapminmax(ts,1,2);	

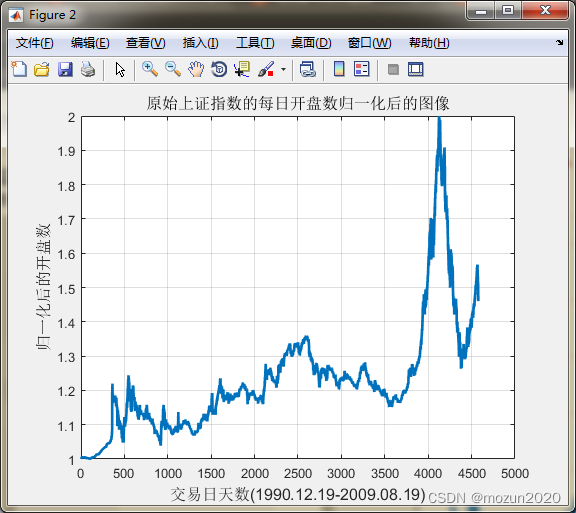
% 画出原始上证指数的每日开盘数归一化后的图像
figure;
plot(TS,'LineWidth',2);
title('原始上证指数的每日开盘数归一化后的图像','FontSize',12);
xlabel('交易日天数(1990.12.19-2009.08.19)','FontSize',12);
ylabel('归一化后的开盘数','FontSize',12);
grid on;
% 对TS进行转置,以符合libsvm工具箱的数据格式要求
TS = TS';

% mapminmax为matlab自带的映射函数
% 对tsx进行归一化
[TSX,TSXps] = mapminmax(tsx,1,2);	
% 对TSX进行转置,以符合libsvm工具箱的数据格式要求
TSX = TSX';

%% 选择回归预测分析最佳的SVM参数c&g

% 首先进行粗略选择: 
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-8,8,-8,8);

% 打印粗略选择结果
disp('打印粗略选择结果');
str = sprintf( 'Best Cross Validation MSE = %g Best c = %g Best g = %g',bestmse,bestc,bestg);
disp(str);

% 根据粗略选择的结果图再进行精细选择: 
[bestmse,bestc,bestg] = SVMcgForRegress(TS,TSX,-4,4,-4,4,3,0.5,0.5,0.05);

% 打印精细选择结果
disp('打印精细选择结果');
str = sprintf( 'Best Cross Validation MSE = %g Best c = %g Best g = %g',bestmse,bestc,bestg);
disp(str);

%% 利用回归预测分析最佳的参数进行SVM网络训练
cmd = ['-c ', num2str(bestc), ' -g ', num2str(bestg) , ' -s 3 -p 0.01'];
model = svmtrain(TS,TSX,cmd);

%% SVM网络回归预测
[predict,mse] = svmpredict(TS,TSX,model);
predict = mapminmax('reverse',predict',TSps);
predict = predict';

% 打印回归结果
str = sprintf( '均方误差 MSE = %g 相关系数 R = %g%%',mse(2),mse(3)*100);
disp(str);

%% 结果分析
figure;
hold on;
plot(ts,'-o');
plot(predict,'r-^');
legend('原始数据','回归预测数据');
hold off;
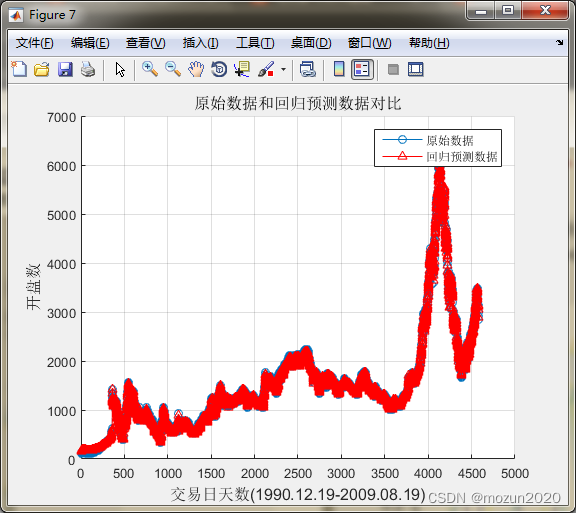
title('原始数据和回归预测数据对比','FontSize',12);
xlabel('交易日天数(1990.12.19-2009.08.19)','FontSize',12);
ylabel('开盘数','FontSize',12);
grid on;

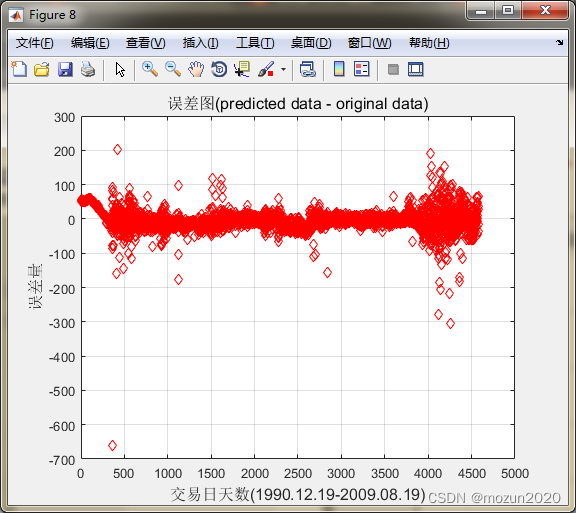
figure;
error = predict - ts';
plot(error,'rd');
title('误差图(predicted data - original data)','FontSize',12);
xlabel('交易日天数(1990.12.19-2009.08.19)','FontSize',12);
ylabel('误差量','FontSize',12);
grid on;

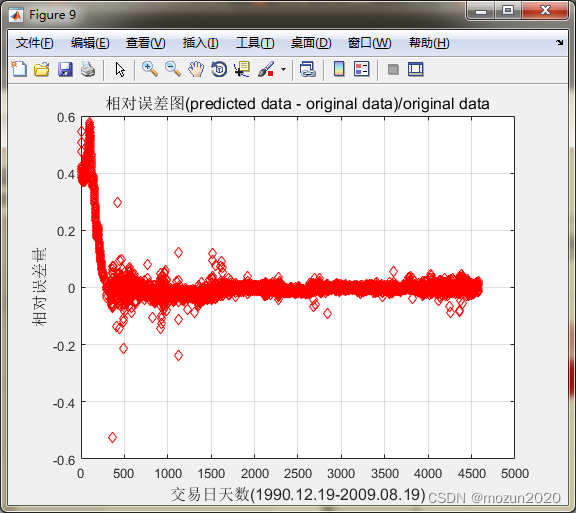
figure;
error = (predict - ts')./ts';
plot(error,'rd');
title('相对误差图(predicted data - original data)/original data','FontSize',12);
xlabel('交易日天数(1990.12.19-2009.08.19)','FontSize',12);
ylabel('相对误差量','FontSize',12);
grid on;
snapnow;
toc;

%% 子函数 SVMcgForRegress.m
function [mse,bestc,bestg] = SVMcgForRegress(train_label,train,cmin,cmax,gmin,gmax,v,cstep,gstep,msestep)
%SVMcg cross validation by faruto

%
% by faruto
%Email:patrick.lee@foxmail.com QQ:516667408 http://blog.sina.com.cn/faruto BNU
%last modified 2010.01.17
%Super Moderator @ www.ilovematlab.cn

% 若转载请注明：
% faruto and liyang , LIBSVM-farutoUltimateVersion 
% a toolbox with implements for support vector machines based on libsvm, 2009. 
% Software available at http://www.ilovematlab.cn
% 
% Chih-Chung Chang and Chih-Jen Lin, LIBSVM : a library for
% support vector machines, 2001. Software available at
% http://www.csie.ntu.edu.tw/~cjlin/libsvm

% about the parameters of SVMcg 
if nargin < 10
    msestep = 0.06;
end
if nargin < 8
    cstep = 0.8;
    gstep = 0.8;
end
if nargin < 7
    v = 5;
end
if nargin < 5
    gmax = 8;
    gmin = -8;
end
if nargin < 3
    cmax = 8;
    cmin = -8;
end
% X:c Y:g cg:acc
[X,Y] = meshgrid(cmin:cstep:cmax,gmin:gstep:gmax);
[m,n] = size(X);
cg = zeros(m,n);

eps = 10^(-4);

bestc = 0;
bestg = 0;
mse = Inf;
basenum = 2;
for i = 1:m
    for j = 1:n
        cmd = ['-v ',num2str(v),' -c ',num2str( basenum^X(i,j) ),' -g ',num2str( basenum^Y(i,j) ),' -s 3 -p 0.1'];
        cg(i,j) = svmtrain(train_label, train, cmd);
        
        if cg(i,j) < mse
            mse = cg(i,j);
            bestc = basenum^X(i,j);
            bestg = basenum^Y(i,j);
        end
        
        if abs( cg(i,j)-mse )<=eps && bestc > basenum^X(i,j)
            mse = cg(i,j);
            bestc = basenum^X(i,j);
            bestg = basenum^Y(i,j);
        end
        
    end
end
% to draw the acc with different c & g
[cg,ps] = mapminmax(cg,0,1);
figure;
[C,h] = contour(X,Y,cg,0:msestep:0.5);
clabel(C,h,'FontSize',10,'Color','r');
xlabel('log2c','FontSize',12);
ylabel('log2g','FontSize',12);
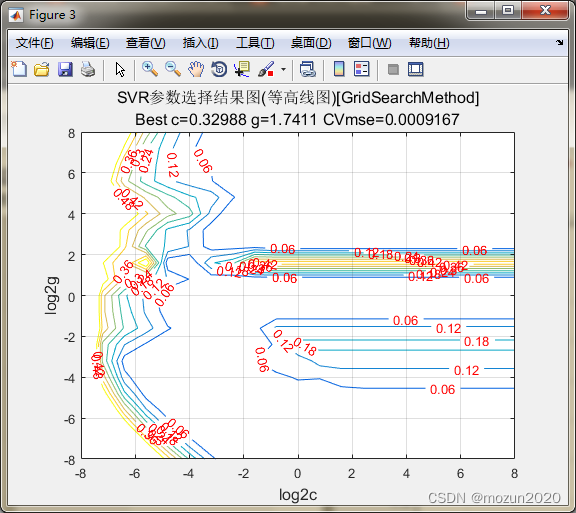
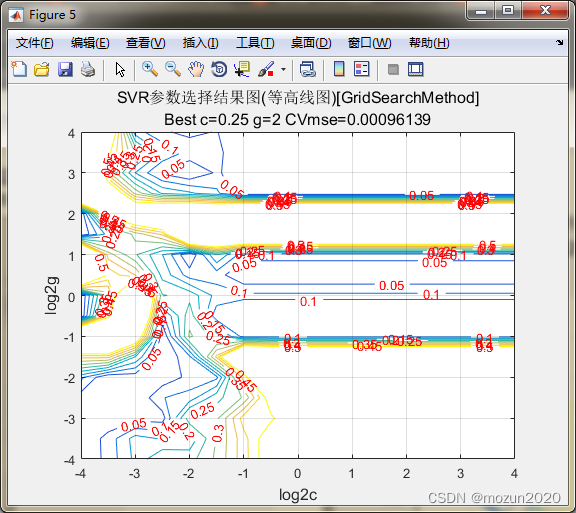
firstline = 'SVR参数选择结果图(等高线图)[GridSearchMethod]'; 
secondline = ['Best c=',num2str(bestc),' g=',num2str(bestg), ...
    ' CVmse=',num2str(mse)];
title({
    
    firstline;secondline},'Fontsize',12);
grid on;

figure;
meshc(X,Y,cg);
% mesh(X,Y,cg);
% surf(X,Y,cg);
axis([cmin,cmax,gmin,gmax,0,1]);
xlabel('log2c','FontSize',12);
ylabel('log2g','FontSize',12);
zlabel('MSE','FontSize',12);
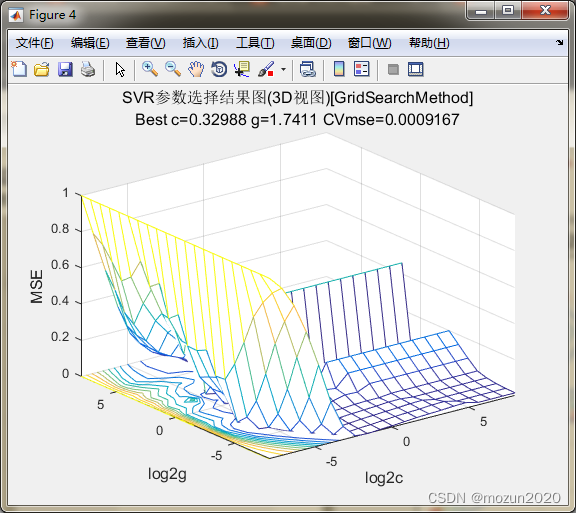
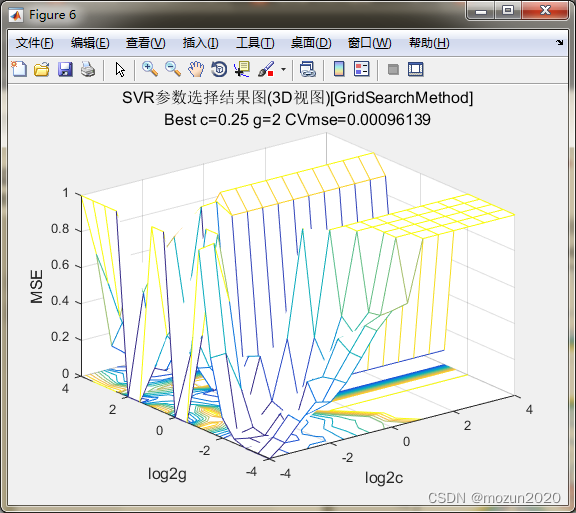
firstline = 'SVR参数选择结果图(3D视图)[GridSearchMethod]'; 
secondline = ['Best c=',num2str(bestc),' g=',num2str(bestg), ...
    ' CVmse=',num2str(mse)];
title({
    
    firstline;secondline},'Fontsize',12);
toc

添加完毕，点击“运行”，开始仿真，输出仿真结果如下：

打印粗略选择结果
Best Cross Validation MSE = 0.000916702 Best c = 0.329877 Best g = 1.7411
打印精细选择结果
Best Cross Validation MSE = 0.000961388 Best c = 0.25 Best g = 2
Mean squared error = 2.35705e-05 (regression)
Squared correlation coefficient = 0.999195 (regression)
均方误差 MSE = 2.35705e-05 相关系数 R = 99.9195%
时间已过 177.247405 秒。

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3. 小结

首先温馨提示股市有风险，投资需谨慎。利用数据模型对股市进行预测分析应该早就有人进行尝试了，但仅仅作为参考就可以了，不建议入戏太深，因为实时指数更多的是受到经济形势，行业动态，公司业绩等等多重因素影响而产生的，并不是根据历史数据建一个模型进行分析就可以掐指一算的。当然从另一个角度来说，如果能够将越来越多的因素都考虑进来，那样进行预测的结果理论上确实应该更加准确一些，但事实是我们都不是上帝，至少目前基本上都是信息孤岛，因此作出的预测与分析不可避免的会存在偏差，也许未来我们挣得会创造出一个接近于上帝的存在，只是这个未来目前来说还是十分遥远的。对本章内容感兴趣或者想充分学习了解的，建议去研习书中第十六章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充，欢迎大家一起学习交流。

猜你喜欢

转载自blog.csdn.net/sinat_34897952/article/details/125213689
今日推荐
周排行
横竖屏切换问题
STM32（十）- SPI
Zookeeper和正则表达式
Codeforces 1325 C. Ehab and Path-etic MEXs (思维) /详解
textarea限制每行可输入固定个数的字符
BGP聚合路由 执行最苛刻的条件
家庭主夫怎么在今年3月27号的市场中利用金叉死叉进行波段操作
FWT+线性基 -- 牛客网暑期ACM多校训练营（第八场）H——Playing games FWT优化dp
XML名命空间
Oracle根据年份获取月份
每日归档
更多
2024-12-22(0)
2024-12-21(0)
2024-12-20(0)
2024-12-19(0)
2024-12-18(0)
2024-12-17(0)
2024-12-16(0)
2024-12-15(0)
2024-12-14(0)
2024-12-13(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022