1.软件版本
matlab2013b
2.系统概述
建立如下被测信号:

被测信号中包含四个振荡模态,在数据窗宽度同样为10s的前提下,利用不同的采样频率做普罗尼计算。结果如表1所示。根据公式的基本表达式:

所以最后,进行估计得到的参数为:
![]()
![]()
![]()
![]()
我们的程序设计中,按照论文中的说明进行设计,对于非连续时间的函数方程式:





3.部分源码
clc;
clear;
close all;
warning off;
pack;
%%
%原始的模拟信号
%原始的模拟信号
Sel = 1; %选择测试信号
n = 0:1:50;
ts = 1:0.0001:length(n)-1;
%你的测试序列
X1 = 10*exp(-0.003.*ts).*cos(0.8*pi.*ts+11*pi/18) +...
1*exp(-0.3.*ts) .*cos(4.5*pi.*ts+1*pi/3) +...
2*exp(-0.3) .*cos(0.9*pi.*ts+1*pi/10) +...
1*exp(-45.*ts).*cos(3*pi.*ts+1*pi/18);
%你的测试序列
X2 = 10*exp(-0.25*ts*0.05).*cos(2*pi*1.5*ts*0.05+pi) + 6*exp(-0.5*ts*0.1).*cos(2*pi*3*ts*0.2+pi/2);
if Sel == 1
Xo = X1;
end
if Sel == 2
Xo = X2;
end
%%
%参数初始化
%参数初始化
Fs = 5;
Time = 100; %模拟时间
Delta = 1/Fs;
dt = 1/Fs;
t = 1:dt:length(n)-1;
%你的测试序列
X1 = 10*exp(-0.003.*t).*cos(0.8*pi.*t+11*pi/18) +...
1*exp(-0.3.*t) .*cos(4.5*pi.*t+1*pi/3) +...
2*exp(-0.3) .*cos(0.9*pi.*t+1*pi/10) +...
1*exp(-45.*t).*cos(3*pi.*t+1*pi/18);
%你的测试序列
X2 = 10*exp(-0.25*t*0.05).*cos(2*pi*1.5*t*0.05+pi) + 6*exp(-0.5*t*0.1).*cos(2*pi*3*t*0.2+pi/2);
if Sel == 1
X = X1;
end
if Sel == 2
X = X2;
end
%%
%普罗尼计算
%普罗尼计算
Xs = func_Prony(X,dt);
figure;
plot(ts,Xo,'r-','LineWidth',2);
hold on;
plot(t,Xs,'k-','LineWidth',1);
hold off;
grid on;
legend('原始数据','Prony预测估计后信号');
xlabel('X');
ylabel('Y');
4.仿真结论
注意,这里论文中你所给的那个公式,貌似有点小错误,这里我们使用了两组公式进行计算,一组是你所提供的公式,一组是我们给的测试数据。
仿真结果如下所示:
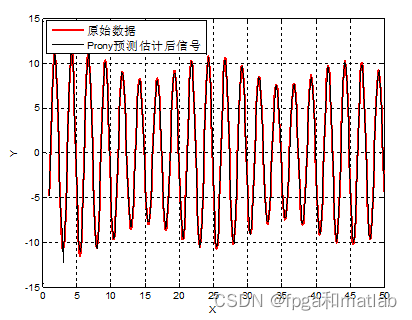
注意,这里我们还用了自己的测试数据进行测试:

参数估计结果如下所示:

对于第一部分的结果,其余你自己修改下参数分布进行测试即可。
5.参考文献
[1]张俊峰, 陈珉, 杨婷,等. 低频振荡参数Prony辨识中的数字滤波器设计[J]. 电力系统及其自动化学报, 2018, 030(012):99-104.A27-6