粒子滤波 particle filter —从贝叶斯滤波到 粒子滤波—Part-III（重要性采样&序贯重要性采样SIS）

粒子滤波 particle filter —从贝叶斯滤波到粒子滤波—Part-III（重要性采样&序贯重要性采样SIS）

原创不易，路过的各位大佬请点个赞

机动目标跟踪/非线性滤波/传感器融合/导航等探讨代码联系WX: ZB823618313

在非线性条件下，贝叶斯滤波面临一个重要问题是状态分布的表达和积分式的求解，由前面章节中的分析可知,对于一般的非线性/非高斯系统,解析求解的途径是行不通的。在数值近似方法中，蒙特卡罗仿真是一种最为通用、有效的手段，粒子滤波就是建立在蒙特卡罗仿真基础之上的，它通过利用一组带权值的系统状态采样来近似状态的统计分布。由于蒙特卡罗仿真方法具有广泛的适用性，由此得到的粒子滤波算法也能适用于一般的非线性/非高斯系统。但是，这种滤波方法也面临几个重要问题，如有效采样(粒子)如何产生、粒子如何传递以及系统状态的序贯估计如何得到等。

简单的理解，粒子滤波就是使用了大量的随机样本，采用蒙特卡洛(MonteCarlo，MC)仿真技术完成贝叶斯递推滤波(Recursive Bayesian Filter)过程。因此本博客从贝叶斯滤波出发，简单介绍粒子滤波PF的出生、即应用

核心思想：是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样，得到一些带有相应权值的随机样本后，在状态观测的基础上调节权值的大小。和粒子的位置，再使用这些样本来逼近状态后验分布，最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束，采用样本形式而不是函数形式对状态概率密度进行描述，使其不需要对状态变量的概率分布进行过多的约束，因而在非线性非高斯动态系统中广泛应用。尽管如此，粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破。

1、贝叶斯滤波

**贝叶斯滤波细节 见Part-I**

考虑离散时间非线性系统动态模型，
$$\begin{gathered} x_k=f(x_{k-1},w_{k-1}) \\ {z}_k=h(x_k,v_k)\text{\hspace{1em}(1)} \end{gathered}$$
其中$x_k$为$k$时刻的目标状态向量，$z_k$为$k$时刻量测向量（传感器数据）。这里不考虑控制器$u_k$。$w_k$和$v_k$分别是过程噪声序列和量测噪声序列。$w_k$和$v_k$为零均值高斯白噪声。

定义$1$ ~ $k$时刻对状态$x_k$的所有测量数据为
$$z^k=[z_1^T,z_2^T,\cdots ,z_k^T{]}^T$$

根据Part-I，$k$时刻状态$x_k$的后验概率密度函数:
$$p(x_k|z^k)=\frac{p(z_k|x_k)p(x_k|z^{k-1})}{p(z_k|z^{k-1})}$$

通过后验分布$p(x_k|z^k)$可以得到$x_k$的最小均方误差(MMSE)估计为
$${\hat{x}}_k=E[x_k|z_k]=\int x_{k}p(x_k|z^k)d{x}_k\text{\hspace{1em}(2)}$$

2、 蒙特卡洛方法MC

**蒙特卡洛近似方法细节 见Part-I**

根据Part-II蒙特卡洛方法，$x_k^{(i)},i=1,2,\cdots ,N$表示从后验概率分布函数$p(x_k|z^k)$采样得到的$N$个独立同分布的样本，则状态的后验概率密度可以通过如下经验公式近似得到:
$$p(x_k|z^k)=\frac{1}{N}\sum _{i=1}^N\delta (x_k-x_k^{(i)})$$
同时后验条件期望可近似表示为
$$\begin{gathered} {\hat{x}}_k=E[x_k|z^k]\approx \hat{E}[x_k|z^k]\approx \frac{1}{N}\sum _{i=1}^N{x}_k^{(i)}, \\ E[g(x_k)|z^k]\approx \hat{E}[g(x_k)|z^k]\approx \frac{1}{N}\sum _{i=1}^{N}g(x_k^{(i)})\text{\hspace{1em}(3)} \end{gathered}$$
蒙特卡洛方法是实现的贝叶斯滤波，得到粒子滤波的桥梁。

3、 重要性采样

需要指出的是，从后验滤波分布$p(x_k|z^k)$进行采样近似只是蒙特卡罗仿真技术的一种特殊形式，实际上更一般的情况是从完整的后验分布$p(x_{1:k}|z_{1:k})$中进行采样、即全状态采样。（这里，$z_{1:k}$和$z^k$等价）

如果我们能够对后验概率密度函数$p(x_{0:k}|z_{1:k})$进行随机采样，便可通过对样本进行加权求和来近似随机变量 $x_k$以及$g(x_k)$的数学期望。

然而通常情况下，对于一般化的非线性系统，无法从后验概率密度函数$p(x_{0:k}|z_{1:k})$中直接进行采样，常规的解决方法是从某一已知的、 容易采样的函数$q(x_{0:k}|z_{1:k})$中间接采样，这种函数称为重要性密度函数(Importance DensityFunction,IDF)， 而这种采样方法称为重要性采样(Importance Sampling, IS)。 为此可以得到

其中$w(x_{0:k})$称之为重要性权值，
$$w(x_{0:k})=\frac{p(z_{1:k}|x_{0:k})p(x_{0:k})}{q(x_{0:k}|z_{1:k})}$$
由于$p(z_{1:k})$是未知的，$E[g(x_{0:k})]$可以进一步表示为

即从概率分布$q(x_{0:k}|z_{1:k})$中采样，得到一组粒子$x_{0:k}^{(i)},i=1,2,\cdots ,N$。将重要性权值$w(x_{0:k})$简记为$w_k$，则后验期望的估计表示为：
$$E[g(x_{0:k})|z^k]\approx \hat{E}[g(x_{0:k})|z^k]\approx \frac{\frac{1}{N}{\sum }_{i=1}^{N}g(x_{0:k}^{(i)})w_k^{(i)}}{\frac{1}{N}{\sum }_{i=1}^N{w}_k^{(i)}}=\sum _{i=1}^{N}g(x_{0:k}^{(i)}){\tilde{w}}_k^{(i)}$$
其中KaTeX parse error: Expected '}', got 'EOF' at end of input: …tilde{w}_k^{(i)为归一化重要性权值：
$${\tilde{w}}_k^{(i)}=\frac{w_k^{(i)}}{{\sum }_{j=1}^N{w}_k^{(j)}}\text{\hspace{1em}(4)}$$

式(4)的估计结果是有偏的，因为其包括-部分估计值。但可以通过以下两个假设获得近收敛和$\hat{E}[g(x_{0:k})|z^k]$的中心极限定理。

• $x_{0:k}^{(i)}$是一组从建议分布中采样得到的粒子， $\hat{E}[g(x_{0:k})|z^k]$存在并且有限。
• 通过后验分布得到的$w_k$和$w_k{g}^2(x_{0:k})$的期望存在且有限。
• 验证第二个假设成立的一一个充分条件是$g(x_{0:k})$的方差和重要性权值有界。因此, 随着$N$趋于无穷大，后验密度函数可以用点估计近似，即
  $$p(x_{0:k}|z_{1:k})=\frac{1}{N}\sum _{i=1}^N\delta (x_{0:k}-x_{0:k}^{(i)}){\tilde{w}}_k^{(i)}$$
  其中$\delta$为狄克里函数。

只要得到了粒子$x_{0:k}^{(i)}$ 及其对应的归一化的重要性权重${\tilde{w}}_k^{(i)}$，便可通过上式近似估计期望$E[g(x_{0:k})|z^k]$。简言之，重要性采样要解决的是原分布难以采样甚至无法采样的问题。不同的粒子都有它们相应的权重，如果粒子权重大，说明信任该粒子比较多。

到这里已经解决了不能从后验概率直接采样的问题，但是上面这种每个粒子的权重都直接计算的方法，效率低，因为每增加一个采样，$p(x_{0:k}|z_{1:k})$都得重新计算，并且还不好计算这个式子。每次计算过程都需要从$1$到$k$时刻的多有测量，不仅时间靠前的测量数据被重复利用，而且随着时间测量增多计算复杂度会急剧上升。

所以求权重时能否避开计算$p(x_{0:k}|z_{1:k})$？而最佳的形式是能够以递推的方式去计算权重，这就是所谓的序贯重要性采样（SIS），粒子滤波的原型。

4、 序贯重要性采样SIS

前面的贝叶斯重要性采样是一种常用的蒙特卡洛积分方法，但其不能直接用来进行递推估计，主要因为估计$p(x_{0:k}|z_{1:k})$的过程需要用到所有的量测信息$k$,然而每次在$k+1$时刻更新量测信息$z_{k+1}$时，则需要重新计算整个状态序列的重要性权值，所以其计算量将随时间的推移而大量增加。为了解决这一问题， 序贯重要性采样( Sequential Importance Sampling，SIS) 方法得以提出。这种方法在$k$时刻采样时不会改动过去的状态序列xx_，而重要性密度函数分解为
$$q(x_{0:k}|z_{1:k})=q(x_k|x_{0:k-1},z_{1:k})q(x_{0:k-1}|z_{1:k-1})\text{\hspace{1em}(5)}$$

系统模型满足以下假设。

• (1)系统状态符合- -阶马尔可夫过程。
• (2)在给定状态下，不同量测值是相互条件独立的。
• (3)初始的先验密度为$p(x_0)$.
  即满足
  $$\begin{gathered} p(x_{0:k})=p(x_0)\prod _{j=1}^{k}p(x_j|x_{j-1}) \\ p(z_{1:k}|x_{0:k})=\prod _{j=1}^{k}p(z_j|x_j) \end{gathered}$$

将上式代入到(5)中，得到重要性权值的递推形式

在给定合适的重要性密度函数$q(x_k|x_{0:k-1},z_{1:k})$的条件下，利用上式可以通.
过递归方法简化重要性权值的计算。

此外，如果重要性密度函数满足
$$q(x_k|x_{0:k-1},z_{1:k})=q(x_k|x_{k-1},z_k)$$
只依赖$x_{k-1},z_k$。

实际上上式很容易满足：因为这是马尔科过程的基本性质。而贝叶斯滤波的非线性系统就为马尔可夫过程。因此他是满足的。

由该函数采样得到粒子：
$$x_k^{(i)}\sim q(x_k|x_{k-1},z_{1:k})$$
并得到归一化重要性权值为：
$${\tilde{w}}_k^{(i)}={\tilde{w}}_{k-1}^{(i)}\frac{p(x_k^{(i)}|x_{k-1}^{(i)})p(z_k|x_k^{(i)})}{q(x_k^{(i)}|x_{k-1}^{(i)},z_k)}\text{\hspace{1em}(6)}$$
其中归一化权值可表示为
$${\tilde{w}}_k^{(i)}=\frac{w_k^{(i)}}{{\sum }_{j=1}^N{w}_k^{(j)}}$$

从而得到后验密度函数的估计为
$$p(x_k|z_{1:k})=\frac{1}{N}\sum _{i=1}^N\delta (x_k-x_k^{(i)}){\tilde{w}}_k^{(i)}$$
其中$\delta$为狄克里函数。

序贯重要性采样算法根据每一步接收到新的量测信息，逐次进行采样粒子和重要性权值的递推，算法步骤如下：

算法：序贯重要性采样SIS
For $i=1:N$
  Step 1: 初始时刻粒子重要性采样 $x_0^{(i)}\sim p(x_0)$
  Step 2: 计算初始时刻重要性权值 ${\tilde{w}}_0^{(i)}=\frac{1}{N}$
End For
SIS核心步骤START：
For $i=1:N$
  Step 3: 采样粒子 $x_k^{(i)}\sim q(x_k|x_{k-1},z_{1:k})$
  Step 4: 根据 $${\tilde{w}}_k^{(i)}={\tilde{w}}_{k-1}^{(i)}\frac{p(x_k^{(i)}|x_{k-1}^{(i)})p(z_k|x_k^{(i)})}{q(x_k^{(i)}|x_{k-1}^{(i)},z_k)}$$
  计算立在的权值${\tilde{w}}_k^{(i)}$
End For
Step 5: 粒子重要性权重归一化
$${\tilde{w}}_k^{(i)}=\frac{w_k^{(i)}}{{\sum }_{j=1}^N{w}_k^{(j)}}$$
SIS核心步骤END.
Step 6: 后验期望估计
$$E[g(x_k)|z^k]\approx \sum _{i=1}^{N}g(x_k^{(i)}){\tilde{w}}_k^{(i)}$$

5. PF的目标跟踪应用：

5.1. 仿真参数

**一、目标模型：CV（细节见另一个博客） **

$$X_{k+1}=\left[\begin{array}{cccc}1& T& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& T\\ 0& 0& 0& 1\end{array}\right]X_k+\left[\begin{array}{cc}{T}^2/2& 0\\ T& 0\\ 0& T^2/2\\ 0& T\end{array}\right]W_k$$

CV CT 模型的具体方程形式见另一个博客

二、测量模型：2D主动雷达
在二维情况下，雷达量测为距离和角度
$$\begin{gathered} r_k^m=r_k+{\tilde{r}}_k \\ {b}_k^m=b_k+{\tilde{b}}_k \end{gathered}$$
其中
$$\begin{gathered} r_k=\sqrt{(x_k-x_0{)}^{+}(y_k-y_0{)}^2)} \\ {b}_k={\tan }^{-1}\frac{y_k-y_0}{x_k-x_0} \end{gathered}$$
$[x_0,y_0]$为雷达坐标，一般情况为0。雷达量测为$z_k=[r_k,b_k{]}^{\prime }$。雷达量测方差为
$$R_k=\text{cov}(v_k)=\left[\begin{array}{cc}{\sigma }_r^2& 0\\ 0& {\sigma }_b^2\end{array}\right]$$

5.2. 跟踪轨迹

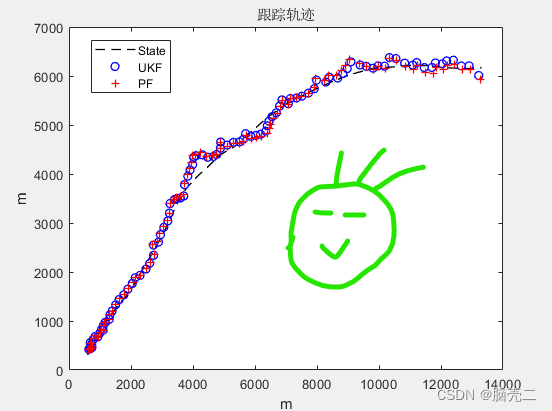
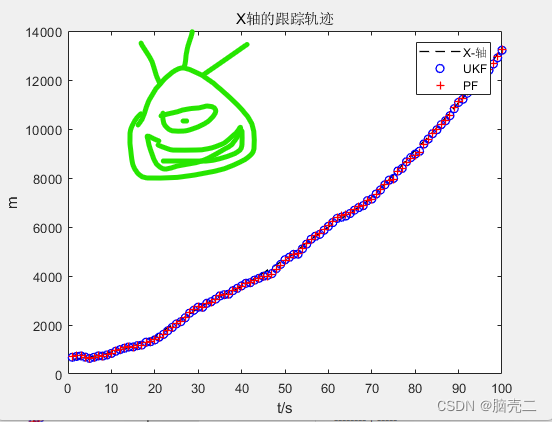
5.3. 跟踪误差（RMSE）

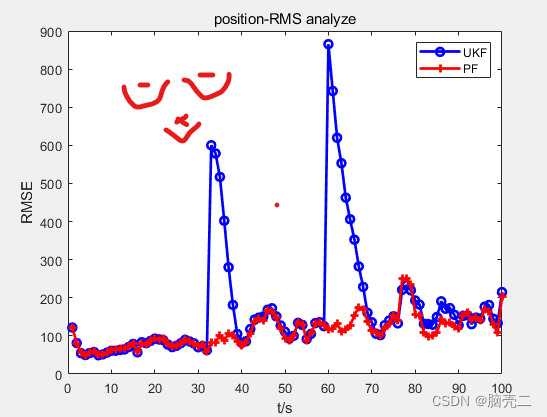
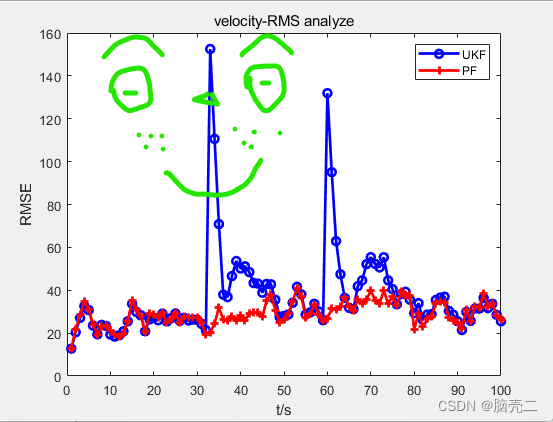
PF的妈妈贝叶斯滤波、基于标准的粒子滤波见Part-I和Part-V

原创不易，路过的各位大佬请点个赞