《MATLAB 神经网络43个案例分析》:第43章 神经网络高效编程技巧——基于MATLAB R2012b新版本特性的探讨
1. 前言
《MATLAB 神经网络43个案例分析》是MATLAB技术论坛(www.matlabsky.com)策划,由王小川老师主导,2013年北京航空航天大学出版社出版的关于MATLAB为工具的一本MATLAB实例教学书籍,是在《MATLAB神经网络30个案例分析》的基础上修改、补充而成的,秉承着“理论讲解—案例分析—应用扩展”这一特色,帮助读者更加直观、生动地学习神经网络。
《MATLAB神经网络43个案例分析》共有43章,内容涵盖常见的神经网络(BP、RBF、SOM、Hopfield、Elman、LVQ、Kohonen、GRNN、NARX等)以及相关智能算法(SVM、决策树、随机森林、极限学习机等)。同时,部分章节也涉及了常见的优化算法(遗传算法、蚁群算法等)与神经网络的结合问题。此外,《MATLAB神经网络43个案例分析》还介绍了MATLAB R2012b中神经网络工具箱的新增功能与特性,如神经网络并行计算、定制神经网络、神经网络高效编程等。
近年来随着人工智能研究的兴起,神经网络这个相关方向也迎来了又一阵研究热潮,由于其在信号处理领域中的不俗表现,神经网络方法也在不断深入应用到语音和图像方向的各种应用当中,本文结合书中案例,对其进行仿真实现,也算是进行一次重新学习,希望可以温故知新,加强并提升自己对神经网络这一方法在各领域中应用的理解与实践。自己正好在多抓鱼上入手了这本书,下面开始进行仿真示例,主要以介绍各章节中源码应用示例为主,本文主要基于MATLAB2015b(32位)平台仿真实现,这是本书第四十三章神经网络高效编程技巧实例,话不多说,开始!
2. MATLAB 仿真示例
打开MATLAB,点击“主页”,点击“打开”,找到示例文件

选中chapter43.m,点击“打开”
chapter43.m源码如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:神经网络高效编程技巧-基于MATLAB R2012b新版本特性的探讨
%环境:Win7,Matlab2015b
%Modi: C.S
%时间:2022-06-21
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Matlab神经网络43个案例分析
% 神经网络高效编程技巧-基于MATLAB R2012b新版本特性的探讨
% by 王小川(@王小川_matlab)
% http://www.matlabsky.com
% Email:sina363@163.com
% http://weibo.com/hgsz2003
% 注意代码为演示脚本,请根据备注分块运行
close all;
clear all
clc
tic
%% 典型的前向神经网络
[x,t]=house_dataset;
net1=feedforwardnet(10);
net2=train(net1,x,t);
y=net2(x);
%% 设置reduction
net=train(net1,x,t,'reduction',10);
y=net(x,'reduction',10);
%% 神经网络并行运算
% CPU并行
% matlabpool open
delete(gcp('nocreate'))
numWorkers = parpool(2)
[x,t]=house_dataset;
net=feedforwardnet(10);
net=train(net,x,t,'useparallel','yes')
y=sim(net,x,'useparallel','yes')
% GPU并行
net=train(net,x,t,'useGPU','yes')
y=sim(net,x,'useGPU','yes')
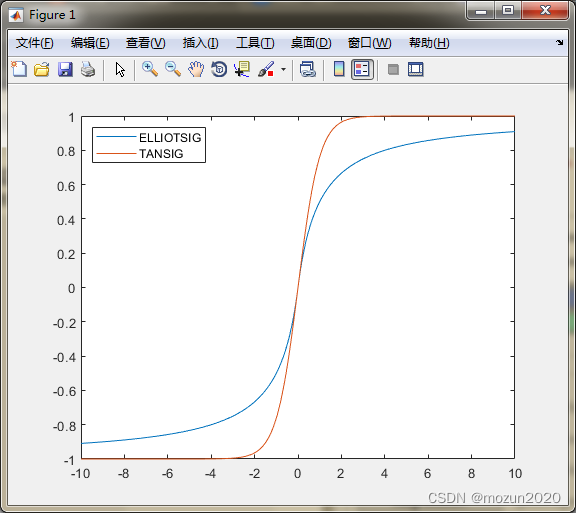
%% Elliot S函数的使用
n=-10:0.01:10;
a1=elliotsig(n);
a2=tansig(n);
h=plot(n,a1,n,a2);
legend(h,'ELLIOTSIG','TANSIG','location','NorthWest')
n = rand(1000,1000);
tic, for i=1:100, a = elliotsig(n); end, elliotsigTime = toc
tic, for i=1:100, a = tansig(n); end, tansigTime = toc
speedup = tansigTime / elliotsigTime
%% 神经网络负载均衡
[x,t] = house_dataset;
Xc = Composite;
Tc = Composite;
Xc{
1} = x(:, 1:100); % First 100 samples of x
Tc{
1} = t(:, 1:100); % First 100 samples of t
Xc{
2} = x(:, 101:506); % Rest samples of x
Tc{
2} = t(:, 101:506); % Rest samples of t
%% 代码组织更新
help nnprocess
help nnweight
help nntransfer
help nnnetinput
help nnperformance
help nndistance
toc
添加完毕,点击“运行”,开始仿真,输出仿真结果如下:
Parallel pool using the 'local' profile is shutting down.
Starting parallel pool (parpool) using the 'local' profile ...
connected to 2 workers.
numWorkers =
Pool - 属性:
Connected: true
NumWorkers: 2
Cluster: local
AttachedFiles: {
}
AutoAddClientPath: true
IdleTimeout: 30 minutes (30 minutes remaining)
SpmdEnabled: true
net =
Neural Network
name: 'Feed-Forward Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 2
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 151
sampleTime: 1
connections:
biasConnect: [1; 1]
inputConnect: [1; 0]
layerConnect: [0 0; 1 0]
outputConnect: [0 1]
subobjects:
input: Equivalent to inputs{
1}
output: Equivalent to outputs{
2}
inputs: {
1x1 cell array of 1 input}
layers: {
2x1 cell array of 2 layers}
outputs: {
1x2 cell array of 1 output}
biases: {
2x1 cell array of 2 biases}
inputWeights: {
2x1 cell array of 1 weight}
layerWeights: {
2x2 cell array of 1 weight}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: 'dividerand'
divideParam: .trainRatio, .valRatio, .testRatio
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mse'
performParam: .regularization, .normalization
plotFcns: {
'plotperform', plottrainstate, ploterrhist,
plotregression}
plotParams: {
1x4 cell array of 4 params}
trainFcn: 'trainlm'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .min_grad, .max_fail, .mu, .mu_dec,
.mu_inc, .mu_max
weight and bias values:
IW: {
2x1 cell} containing 1 input weight matrix
LW: {
2x2 cell} containing 1 layer weight matrix
b: {
2x1 cell} containing 2 bias vectors
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
y =
1 至 11 列
26.5649 23.8963 35.3167 34.0331 33.2050 26.6177 19.4666 17.6496 16.9333 17.5074 17.8289
12 至 22 列
18.4232 20.2884 19.2130 18.1789 19.2407 21.1541 17.4378 18.4759 18.1597 15.8114 17.2226
23 至 33 列
17.2158 16.0054 16.4798 15.9178 16.3531 16.5772 18.5624 19.9107 15.7658 17.0476 16.2111
34 至 44 列
16.0783 16.2199 20.9717 21.3573 22.4374 24.5116 31.6593 37.3553 30.6522 23.5682 23.8258
45 至 55 列
22.8457 21.6117 22.9742 18.7009 17.5504 19.2179 20.7874 22.4802 26.8306 21.2091 23.8159
56 至 66 列
37.3504 25.1582 31.1299 23.4489 21.9053 19.0342 17.4677 23.4439 25.3006 30.9247 28.1945
67 至 77 列
22.5599 22.0387 19.7366 21.3109 26.9079 22.4068 24.9839 25.2604 29.6492 22.1388 18.9827
78 至 88 列
21.7213 19.7240 21.6383 28.7301 23.4959 25.2390 22.9466 24.8965 27.2614 24.2773 24.2914
89 至 99 列
28.2512 31.0355 25.2934 24.2401 24.7488 27.3502 20.3813 26.9904 23.1447 40.5675 44.5740
100 至 110 列
34.1028 22.8109 23.9780 21.2773 19.9033 20.0861 18.9174 19.4450 20.6953 20.5032 19.9361
111 至 121 列
23.8382 21.7507 18.5984 18.5463 20.1065 17.7629 20.5600 18.9054 18.9263 20.2244 21.2653
122 至 132 列
21.9477 19.2307 16.7994 19.0573 21.2896 16.4173 16.8229 19.1419 16.0063 20.3104 19.8476
133 至 143 列
20.7054 16.9056 15.5118 17.6302 17.1318 19.5664 15.9773 17.4037 15.7664 13.6104 14.2766
144 至 154 列
16.8868 15.0215 7.7864 15.7275 14.3187 13.1964 16.7919 20.9003 18.7391 14.3712 17.3107
155 至 165 列
17.2587 17.5046 13.5260 38.6815 28.2783 25.5819 29.7610 49.1533 47.4279 51.0366 22.1065
166 至 176 列
23.6777 50.0421 20.4957 23.4337 23.8454 18.4839 20.5531 23.6133 25.1760 24.7953 29.9514
177 至 187 列
25.4153 24.4943 28.8963 37.5006 41.4320 29.9014 35.9078 29.6126 23.4604 27.7544 46.9291
188 至 198 列
32.0717 29.8403 34.1304 30.3110 27.6823 33.9577 32.6796 29.8632 48.0170 37.3538 31.3165
199 至 209 列
35.0443 34.7285 35.7639 24.4859 42.1004 48.5204 51.6130 22.4677 21.9444 18.1892 21.9470
210 至 220 列
17.7342 20.7005 18.0920 20.6546 24.4089 27.7455 22.6432 24.4801 25.0930 18.9495 28.9056
221 至 231 列
26.7565 21.5714 26.1969 24.7401 43.4779 47.2852 40.4343 29.2835 45.7140 32.3809 22.4439
232 至 242 列
32.2503 44.9441 43.2386 26.8292 23.5077 25.0582 32.1496 25.7791 25.4367 25.2751 20.2267
243 至 253 列
21.5403 24.3852 17.0162 16.6969 21.7378 19.2453 22.6710 26.1453 25.8987 26.7321 26.9997
254 至 264 列
36.8934 22.9069 19.3476 41.6412 54.1393 36.7100 32.0374 34.7428 39.4294 48.8169 34.8423
265 至 275 列
35.5150 23.1172 29.9240 50.3426 47.1693 18.7587 22.1208 25.4768 26.0070 37.2942 32.9633
276 至 286 列
32.1191 34.1121 33.0264 28.0307 37.2538 46.2947 37.4417 43.9732 53.1790 32.5625 25.4412
287 至 297 列
20.5018 23.1884 23.1355 25.3114 35.6611 38.2709 33.5755 24.2597 22.5439 30.9491 28.5340
298 至 308 列
19.2980 24.7290 32.5504 27.3564 26.2345 27.5806 33.5211 36.9534 30.7142 36.4146 30.9553
309 至 319 列
24.2694 18.6600 18.0868 22.5957 18.1427 19.9788 20.6990 17.0862 17.2648 17.7313 20.5753
320 至 330 列
19.4429 23.5494 23.1678 21.3442 17.7827 24.5917 24.7210 23.4610 20.6296 22.4372 24.7429
331 至 341 列
20.9764 19.2289 21.0957 23.3897 22.7596 20.7233 20.4455 19.6999 22.2372 21.5693 20.8254
342 至 352 列
33.8562 19.6238 25.9744 31.4417 18.3665 17.4625 29.1199 28.0675 29.4162 24.9090 25.7243
353 至 363 列
19.7282 31.0909 18.9530 24.5006 19.2800 18.3343 15.2951 22.6964 23.9613 21.6809 22.9029
364 至 374 列
20.4064 23.7425 34.3384 24.2606 33.7902 50.6635 57.1621 57.2010 36.1846 46.4003 9.5275
375 至 385 列
5.6477 20.9966 15.0029 15.6707 11.8745 11.9566 10.6016 12.5754 9.9299 9.9765 8.4788
386 至 396 列
7.5003 3.5342 9.7833 5.1151 11.7370 16.1919 19.0900 7.0987 20.7425 16.6463 16.9238
397 至 407 列
16.7475 14.1719 4.5413 17.2885 6.7930 12.2707 13.4259 8.8577 11.2502 3.1350 12.0974
408 至 418 列
28.4709 19.2913 19.4778 18.4398 18.9188 15.3099 17.9595 3.5736 8.9826 9.7391 8.9614
419 至 429 列
5.4574 11.0193 17.9750 19.4023 22.6472 13.3676 16.3755 10.2455 14.7707 10.0486 12.2779
430 至 440 列
10.8847 18.6243 17.2836 21.6089 16.2555 14.8827 10.0539 12.3158 8.2350 7.8187 12.0014
441 至 451 列
10.8312 13.7364 16.6852 13.6024 9.7569 9.5413 16.7027 16.0780 12.0619 13.1249 13.2298
452 至 462 列
14.6964 17.0095 15.1535 11.4741 13.7664 12.2353 12.9877 17.3928 19.7702 17.3746 20.4944
463 至 473 列
21.1293 22.6934 23.5661 23.5699 13.5559 15.4246 14.6432 22.0109 16.3024 23.3346 20.9164
474 至 484 列
26.2760 18.4605 15.4811 15.5182 10.0277 15.1480 22.2057 23.2604 26.9101 26.8724 24.2792
485 至 495 列
23.7287 23.7627 14.8351 25.5489 13.2138 5.5286 -0.9328 12.9850 16.7500 21.8281 24.9077
496 至 506 列
23.7792 19.6660 18.9583 21.3667 19.2257 19.5222 21.4640 18.9323 25.4267 23.4556 18.7017
NOTICE: Jacobian training not supported on GPU. Training function set to TRAINSCG.
net =
Neural Network
name: 'Feed-Forward Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 2
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 151
sampleTime: 1
connections:
biasConnect: [1; 1]
inputConnect: [1; 0]
layerConnect: [0 0; 1 0]
outputConnect: [0 1]
subobjects:
input: Equivalent to inputs{
1}
output: Equivalent to outputs{
2}
inputs: {
1x1 cell array of 1 input}
layers: {
2x1 cell array of 2 layers}
outputs: {
1x2 cell array of 1 output}
biases: {
2x1 cell array of 2 biases}
inputWeights: {
2x1 cell array of 1 weight}
layerWeights: {
2x2 cell array of 1 weight}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: 'dividerand'
divideParam: .trainRatio, .valRatio, .testRatio
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mse'
performParam: .regularization, .normalization
plotFcns: {
'plotperform', plottrainstate, ploterrhist,
plotregression}
plotParams: {
1x4 cell array of 4 params}
trainFcn: 'trainscg'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .min_grad, .max_fail, .sigma,
.lambda
weight and bias values:
IW: {
2x1 cell} containing 1 input weight matrix
LW: {
2x2 cell} containing 1 layer weight matrix
b: {
2x1 cell} containing 2 bias vectors
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
y =
1 至 11 列
26.1052 23.9302 35.3771 33.8291 33.0630 26.3830 19.0359 17.5569 16.8636 17.2882 17.7174
12 至 22 列
18.2294 19.6969 18.9601 18.1081 18.8878 20.4445 17.3256 17.8212 17.9337 15.7446 17.1369
23 至 33 列
17.1539 15.9448 16.4072 15.7874 16.2701 16.4893 18.5389 19.8947 15.6949 16.9973 16.0209
34 至 44 列
15.9942 16.1378 20.6872 20.9464 21.7688 23.8159 29.7893 35.4520 30.0925 22.9551 23.2047
45 至 55 列
22.3536 21.0165 22.4210 18.4536 17.3079 18.6898 20.1176 22.0121 26.0986 20.4135 22.7862
56 至 66 列
35.7018 23.5710 29.4466 22.6233 21.1450 18.4573 17.2552 23.0774 24.6646 30.6855 26.2513
67 至 77 列
21.0169 21.1902 18.9905 20.5382 26.1687 21.6999 24.1548 24.5064 28.6841 21.8397 18.9234
78 至 88 列
21.3944 19.5442 21.1502 27.8482 23.1162 24.2972 22.1583 24.4150 26.9827 23.7395 23.8799
89 至 99 列
28.5188 30.9379 25.0518 24.1241 24.1114 26.0978 20.1648 26.7065 22.8512 40.9028 44.2740
100 至 110 列
34.0684 22.8012 23.9517 21.2881 19.8664 20.0481 18.9029 19.4613 20.6748 20.4826 19.9206
111 至 121 列
23.6942 21.7098 18.6340 18.5892 20.0501 17.7523 20.4816 18.8208 18.8787 20.1178 21.0919
122 至 132 列
21.9772 19.2721 16.8112 19.0977 21.3317 16.4186 17.0111 19.3549 16.2832 20.4699 20.0176
133 至 143 列
20.8380 17.1623 15.7846 17.9559 17.4110 19.7630 16.2902 17.6726 16.3440 14.2640 14.0424
144 至 154 列
17.3563 15.7702 8.2714 15.2524 15.1402 13.9131 16.7177 20.2764 17.9912 13.7273 16.7480
155 至 165 列
16.6946 16.9625 13.1041 38.2405 27.8189 24.7960 29.1962 48.5739 47.1319 50.8078 21.7652
166 至 176 列
23.4894 49.6868 20.1898 23.2567 23.6505 18.3392 20.3294 23.7072 25.2985 24.6221 29.4758
177 至 187 列
24.9921 24.4312 28.9922 37.4922 41.8402 29.7498 36.3731 29.9761 23.3787 27.5658 46.8859
188 至 198 列
30.8714 28.3625 32.8117 28.7918 26.3096 32.4524 31.1045 28.4310 46.4336 35.7800 29.8718
199 至 209 列
33.5372 32.8610 33.9137 22.8331 40.0832 46.7982 49.8822 21.7295 21.5281 17.9203 21.9977
210 至 220 列
17.8236 20.8489 18.2242 20.6413 23.7560 27.8925 22.0683 23.9388 25.2703 19.2414 28.8964
221 至 231 列
27.0582 21.9844 26.4298 24.8221 43.9769 47.8780 40.9457 29.5095 45.1444 31.6332 22.2249
232 至 242 列
32.5266 45.3645 43.6243 26.8567 23.2040 25.2528 32.3439 24.7259 24.6634 24.6140 19.6113
243 至 253 列
20.8490 23.2388 16.6810 16.2319 21.0220 19.0348 22.0843 25.3862 24.9961 25.7506 26.3620
254 至 264 列
36.5440 21.4507 17.8251 39.9753 54.2588 37.1643 32.4035 34.9698 39.7393 49.0541 35.2641
265 至 275 列
35.8699 23.0767 30.1698 50.3990 46.9021 18.6542 21.3872 24.4769 25.4980 37.2529 31.8644
276 至 286 列
31.1094 33.5341 31.9123 26.8866 37.1073 46.1695 37.1640 43.8987 51.6298 30.7881 24.2471
287 至 297 列
19.1356 22.0448 22.1756 24.0929 33.8793 36.5313 31.7265 23.6091 22.0843 30.5687 28.4142
298 至 308 列
18.8895 23.1113 30.7386 26.0831 25.3413 26.4507 32.2505 36.1615 30.0673 36.0605 30.4683
309 至 319 列
24.3732 18.5362 17.4719 22.0675 18.1226 19.9667 20.7546 16.9316 17.1622 17.5083 20.3804
320 至 330 列
19.0718 23.1399 22.7882 20.8261 17.5458 24.0109 23.9426 22.7860 20.0667 21.6882 23.8885
331 至 341 列
20.2886 18.2118 20.0401 22.8820 22.2405 20.0701 19.8085 19.1981 21.5486 20.9327 20.3238
342 至 352 列
33.1751 19.2608 24.8264 29.7636 17.9061 17.0023 27.4173 26.4054 28.2609 23.8518 24.5448
353 至 363 列
18.5078 29.8888 17.7396 23.1480 18.1294 16.9033 13.7941 21.0323 22.1927 20.2551 21.7974
364 至 374 列
18.9514 21.6398 33.1362 23.2493 32.6777 49.5711 54.8847 54.9243 35.6095 44.3276 12.2624
375 至 385 列
8.7500 20.5041 15.3502 16.2838 12.8156 12.9389 11.0646 13.2939 11.1418 11.3080 9.3977
386 至 396 列
9.4044 5.5720 11.4089 7.0473 12.6022 16.2866 18.3116 8.5392 20.2570 16.5592 16.8953
397 至 407 列
16.8658 14.8100 6.4503 17.4849 8.1966 12.8346 13.7658 9.5697 11.7624 4.4385 14.0421
408 至 418 列
28.0355 20.5128 18.8668 16.7771 17.7931 14.9449 17.9058 3.7976 8.3035 8.8910 8.4500
419 至 429 列
4.7895 9.8625 17.1620 18.5163 21.9529 12.3248 14.9401 9.3703 13.2836 8.7765 11.1714
430 至 440 列
10.0530 17.4321 16.2562 19.9220 14.7849 13.5412 9.1382 11.0436 7.4455 7.2669 12.2955
441 至 451 列
10.9708 13.4480 16.3358 13.3781 9.3123 8.6123 15.8215 15.4831 12.0833 12.6201 11.9444
452 至 462 列
14.1960 16.3897 14.5162 10.3416 12.4374 11.0103 11.5851 16.0108 18.6785 16.0854 19.4676
463 至 473 列
19.8734 21.4142 22.0120 21.6229 12.3140 16.0234 14.2611 20.8949 16.3751 23.6808 20.2390
474 至 484 列
24.7399 19.2356 16.1301 16.0267 11.3811 15.7718 21.8281 22.2273 25.8419 25.7634 22.5569
485 至 495 列
21.9501 22.0320 14.5170 23.9251 15.4170 8.1912 2.2122 15.2351 18.8811 21.5379 24.5755
496 至 506 列
23.7203 19.7834 18.8922 21.2567 19.1922 19.5051 21.3002 18.7973 25.5533 23.5363 18.6050
elliotsigTime =
0.4284
tansigTime =
0.8825
speedup =
2.0603
Neural Network Toolbox Processing Functions.
General Data Preprocessing
fixunknowns - Processes matrix rows with unknown values.
mapminmax - Map matrix row minimum and maximum values to [-1 1].
mapstd - Map matrix row means and deviations to standard values.
processpca - Processes rows of matrix with principal component analysis.
removeconstantrows - Remove matrix rows with constant values.
removerows - Remove matrix rows with specified indices.
Data Preprocessing for Specific Algorithms
lvqoutputs - Define settings for LVQ outputs, without changing values.
Main nnet function list.
Neural Network Toolbox Weight Functions.
Weight functions
convwf - Convolution weight function.
dotprod - Dot product weight function.
negdist - Negative distance weight function.
normprod - Normalized dot product weight function.
scalprod - Scalar product weight function.
Distance functions can be used as weight functions
boxdist - Box distance function.
dist - Euclidean distance weight function.
linkdist - Link distance function.
mandist - Manhattan distance function.
Main nnet function list.
Neural Network Toolbox Transfer Functions.
compet - Competitive transfer function.
elliotsig - Elliot sigmoid transfer function.
hardlim - Positive hard limit transfer function.
hardlims - Symmetric hard limit transfer function.
logsig - Logarithmic sigmoid transfer function.
netinv - Inverse transfer function.
poslin - Positive linear transfer function.
purelin - Linear transfer function.
radbas - Radial basis transfer function.
radbasn - Radial basis normalized transfer function.
satlin - Positive saturating linear transfer function.
satlins - Symmetric saturating linear transfer function.
softmax - Soft max transfer function.
tansig - Symmetric sigmoid transfer function.
tribas - Triangular basis transfer function.
Main nnet function list.
Neural Network Toolbox Net Input Functions.
netprod - Product net input function.
netsum - Sum net input function.
Main nnet function list.
Neural Network Toolbox Performance Functions.
mae - Mean absolute error performance function.
mse - Mean squared error performance function.
sae - Sum absolute error performance function.
sse - Sum squared error performance function.
crossentropy - Cross-entropy performance.
msesparse - Mean squared error performance function with L2 weight and sparsity regularizers.
Main nnet function list.
Neural Network Toolbox Distance Functions.
boxdist - Box distance function.
dist - Euclidean distance weight function.
linkdist - Link distance function.
mandist - Manhattan distance function.
Main nnet function list.
时间已过 3.748946 秒。
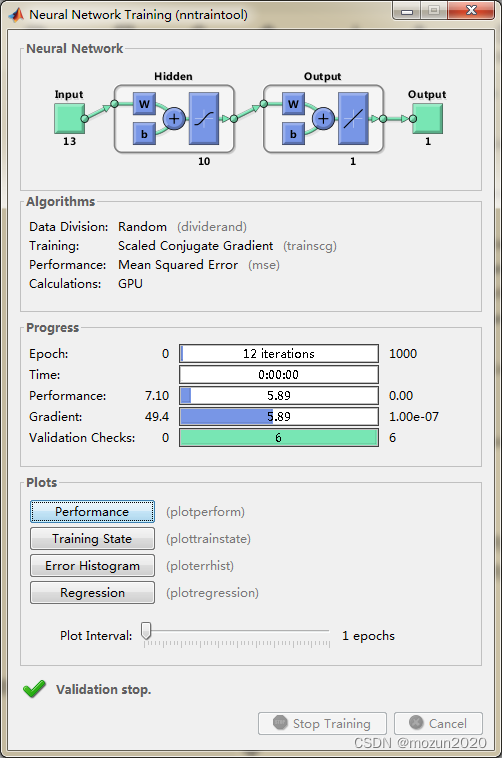
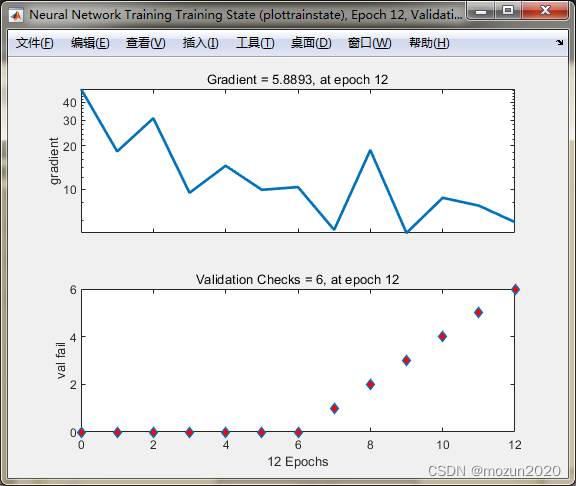
依次点击Plots框下的Performance,Training State,Error Histogram,Regression可得到以下图示:

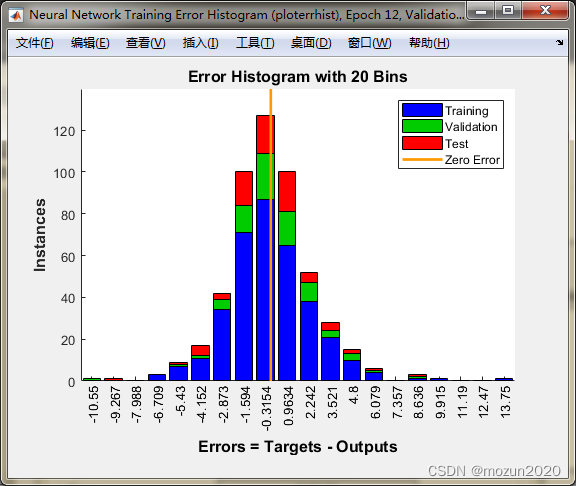
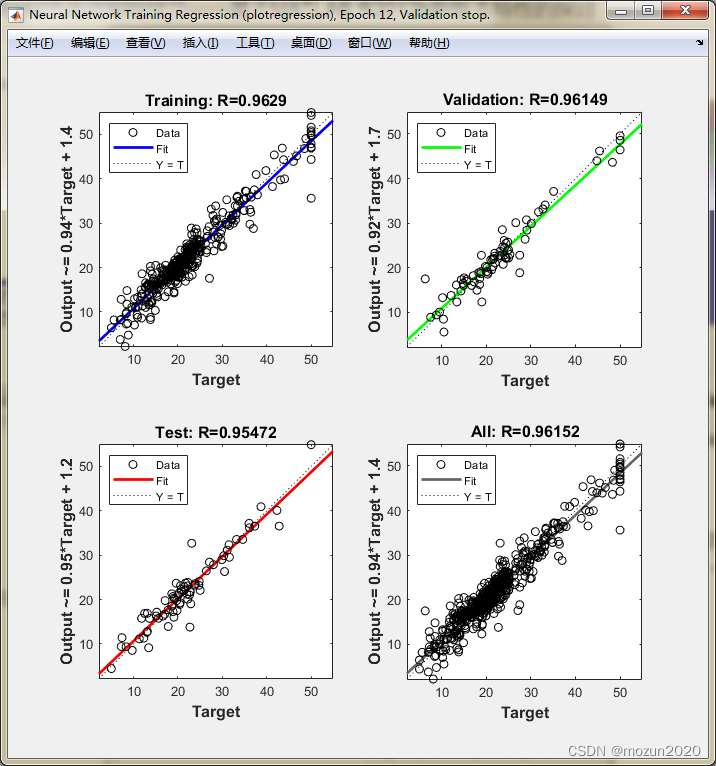
3. 小结
并行计算相关函数与数据调用在MATLAB2015版本之后都有升级,所以需要对源码进行调整再进行仿真,本文示例均根据机器情况与MATLAB版本进行适配。对本章内容感兴趣或者想充分学习了解的,建议去研习书中第四十三章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充,欢迎大家一起学习交流。