2020 年第十届MathorCup高校数学建模挑战赛
B题养老服务床位需求预测与运营模式研究
原题再现:
家家都有老人,人人都会变老。随着时间的推移,我国老龄人口逐渐增多,老龄化的社会问题越来越突出。由于我国人口基数大,养老需求的层次也不相同,解决养老服务问题已是迫在眉睫。解决这个社会问题的一个有效途径是通过政府和各方面的努力,来尽可能的不断满足老年人的养老服务需求。我国目前的养老模式主要以家庭养老、社区养老、机构养老为主,其中机构养老的类型有公办养老院、民办养老院、公建民营养老院等,都对养老服务事业做出了不同的贡献。但是现有的养老服务床位供给还远远不能满足社会的需求,增加养老服务床位是一个急待解决的现实问题。从政府角度来说,合理估计养老服务中床位的需求,制定合理的养老服务床位发展规划,是构建和谐社会、幸福社会的重要组成部分。从企业角度出发,养老服务床位的增加也为企业提供了一个“商机”。
请你通过数学建模和数据分析,对上述背景进行量化建模,解答以下问题:
问题 1:根据我国的人口数量、结构和消费水平等多种因素,预测养老服务床位数量的市场需求规模及其分类。
问题 2:从企业角度出发,结合现有养老服务床位的数量和结构,分析、建立合适的模型,来发现并分析养老服务床位增加中的“商机”。
问题 3:建立一个合适的数学模型,从政府的角度出发,设计一个既能基本满足社会需求,又能持续发展养老服务事业,同时还能促进社会就业的养老服务床位运营的商业模式(养老服务的收入来源目前主要有经营收入、政府补贴、社会捐赠等)。
问题 4:试用精炼的数学语言归纳总结本题中最关键的数学建模问题及其算法。以你们的模型及其结论为科学依据,对政府管理部门针对养老床位规划问题提出合理的建议。以下附件数据仅供参考,可以在这些数据的基础上根据需要查阅更多数据。
模型的建立与求解
模型假设
1.假设在本文多元回归模型中,其它因素不会对养老服务床位产生显著影响;
2.假设老年人口中低保人数比例与全国总人口中低保人数比例相同;.
3.假设各类型床位建设造价相同;
4.假设养老服务市场不会出现突变情况;
5.假设对于养老服务市场,社会捐赠的收入来源对与总收入而言无显著影响; .
问题一要求预测未来养老服务床位数量的市场需求规模及其分类情况。
本文首先考虑确定影响养老服务床位市场变动的主要因素,并从人口数量与结构、居民观念、社会投入(重视程度)三方面进行因素分析,初步确定以下因素: (a)城乡人口比、65岁及以上人口(万人)、老年抚养比;(b)参加养老保险人数、居民人均可支配收入;©社会服务组织职工人数、社会服务机构组织数。对于未来养老服务床位数量的市场需求规模,由于它为连续型数值变量并受多因素影响,本文尝试采用基于最小二乘法的多元线性回归模型进行预测。通过模型诊断以及检验,确定最终影响变量与多重线性回归方程,并以此进行未来(2021年)养老服务床位数量预测。考虑到缺少未来各影响因素的具体数据,本文将通过时间序列模型进行相关数据预测。对于未来养老服务床位分类,本文选取消费水平为主要分类依据,将养老服务床位分为公办保障型、公办普通型、民办普通型与民办VIP型。具体而言,本文将利用时间序列模型预测得到2021年老年低保人数,并以此确定公办保障型床位数量,同时,通过查阅资料相关资料,确定合适的民办型床位数量。
根据我国人口数量、消费水平、社会福利等多方面因素,预测养老服务床位数量的需求规模,并对养老服务床位需求状况进行分类。首先,建立了基于 Lasso回归的预测模型,选取多个影响因素指标,分别考虑了人口结构因素:老年抚养比;经济因素:人均可支配收入、恩格尔系数、城镇化率;政策因素:人均养老保险基金支出。
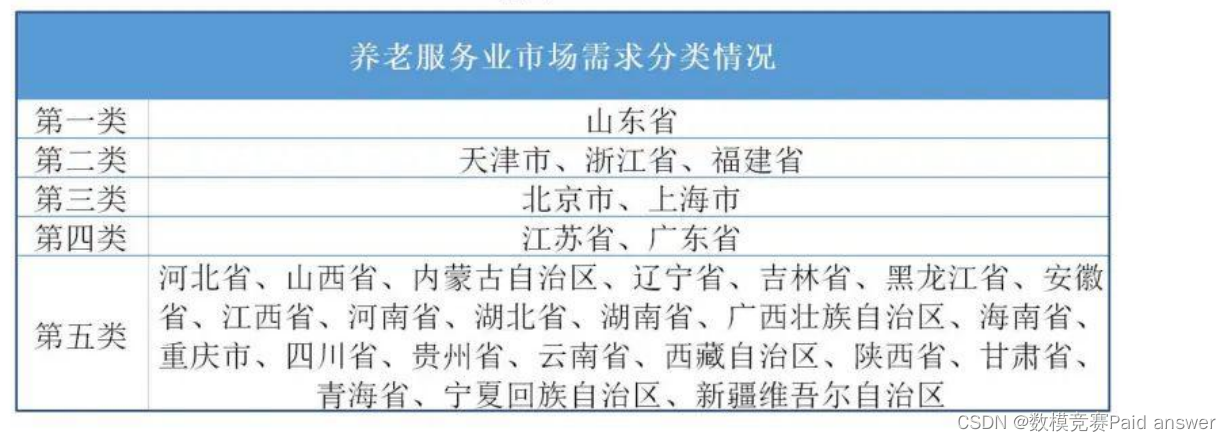
根据 2005年以来这些数据的变化情况,利用时间序列 ARIMA(p,b,q) 模型进行预测。然后,对全国所有省、市、自治区(不含港澳台)根据经济发展状况和老年人口状况进行分类汇总。
影响因素的选择
为了尽可能多地从各个方面综合分析影响养老服务床位数量的因素,根据附件1-3和在线数据,本文选取了养老抚养比、人均可支配收入、恩格尔系数等指标,对近五年城镇化率和人均养老保险基金支出进行分析。各预测指标的意义和计算方法如下:
(1) 老年抚养比
老年抚养比是指人口中老年人数量与工作年龄人口数量的比率,用于反映社会老龄化程度和老年人的抚养程度。老年抚养比越高,意味着年轻人需要抚养更多的老年人,而年轻人的时间有限,老年人更倾向于选择社区养老金或机构养老金。
(2) 人均可支配收入
人均可支配收入反映了经济发展水平,被认为是消费支出的最重要决定因素。当人们有更多的可支配收入时,老年人对养老金服务有更多的需求,并能够支付与养老金相关的服务,这可以促进养老金服务床位的增长。
(3) 恩格尔系数
恩格尔系数是食品总支出占个人消费总支出的比例。随着社会的发展,食品支出在国民平均收入中的比例将越来越大,随着国家的繁荣,这一比例将下降。恩格尔系数越小,选择除食物以外的其他消费的老年人比例越大,倾向于选择更高的生活质量,并选择更好的养老服务机构,从而推动了养老床位的增长。
(4) 城市化率
养老机构通常分布在城市。随着城市化的浪潮,越来越多的老年人居住在城市。中国养老的重点将从农村转移到城市,这将为城市养老服务业带来强大动力。
(5) 人均养恤基金支出
人均养老保险基金通常由经济发展水平和国家宏观政策决定,这间接反映了老年人的平均经济状况,进而影响到是否在养老院和养老床位提供养老服务
随着对老年人需求的不断增加,近年来老年护理行业没有得到迅速的认识和发展。养老专业人才的缺乏已成为制约养老产业发展的重要因素。严峻的就业形势和对养老服务人员的充分需求促使社会培养更多相关人才。养老服务发展需求强劲,需求巨大自然意味着其劳动力吸收能力强。养老服务业的发展也会带来强大的外部驱动效应,不仅是指对养老服务业、老年食品、老年医疗等产业的推动,还进一步带动老年旅游业、金融产品、保险业等产业的发展,以促进就业的发展。
多目标规划模型:

单篇论文缩略图:

程序代码
def regression_diagnostics(reg,lm):
'''
reg: 回归数据
lm: 拟合模型
'''
results = pd.DataFrame({
'index': reg['log'], # y实际值
'resids': lm.resid, # 残差
'std_resids':lm.resid_pearson, # 方差标准化的残差
'fitted': lm.predict() # y预测值
})
print(results.head())
# 1. 图表分别显示
## raw residuals vs. fitted
# 残差拟合图:横坐标是拟合值,纵坐标是残差。
residsvfitted = plt.plot(results['fitted'], results['resids'], 'o')
l = plt.axhline(y = 0, color = 'grey', linestyle = 'dashed') # 绘制y=0水平线
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted')
plt.show(residsvfitted)
## q-q plot
# 残差QQ图:用来描述残差是否符合正态分布。
qqplot = sm.qqplot(results['std_resids'], line='s')
plt.xlabel('Theoretical quantiles')
plt.ylabel('Sample quantiles')
plt.title('Normal Q-Q')
plt.show(qqplot)
## scale-location
# 标准化的残差对拟合值:对标准化残差平方根和拟合值作图,横坐标是拟合值,纵坐标是标准化后的残差平方根。
scalelocplot = plt.plot(results['fitted'], abs(results['std_resids'])**.5, 'o')
plt.xlabel('Fitted values')
plt.ylabel('Square Root of |standardized residuals|')
plt.title('Scale-Location')
plt.show(scalelocplot)
## residuals vs. leverage
# 标准化残差对杠杆值:通常用Cook距离度量的回归影响点。
residsvlevplot = sm.graphics.influence_plot(lm, criterion = 'Cooks', size = 2)
plt.xlabel('Obs.number')
plt.ylabel("Cook's distance")
plt.title("Cook's distance")
plt.show(residsvlevplot)
plt.close()
# 2 绘制在一张画布
fig = plt.figure(figsize = (10, 10), dpi = 100)
ax1 = fig.add_subplot(2, 2, 1)
ax1.plot(results['fitted'], results['resids'], 'o')
l = plt.axhline(y = 0, color = 'grey', linestyle = 'dashed')
ax1.set_xlabel('Fitted values')
ax1.set_ylabel('Residuals')
ax1.set_title('Residuals vs Fitted')
ax2 = fig.add_subplot(2, 2, 2)
sm.qqplot(results['std_resids'], line='s', ax = ax2)
ax2.set_title('Normal Q-Q')
ax3 = fig.add_subplot(2, 2, 3)
ax3.plot(results['fitted'], abs(results['std_resids'])**.5, 'o')
ax3.set_xlabel('Fitted values')
ax3.set_ylabel('Sqrt(|standardized residuals|)')
ax3.set_title('Scale-Location')
ax4 = fig.add_subplot(2, 2, 4)
sm.graphics.influence_plot(lm, criterion = 'Cooks', size = 2, ax = ax4)
plt.tight_layout()