邮递员问题
旅行商问题:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。(遍历点,回到起点)
哈密顿路径 哈密顿图
中国邮递员问题:邮差要设法找到一条最短路径,可以走过此地区所有的街道,且最后要回到出发点。 (遍历边,回到起点)
欧拉路径 欧拉图
旅行商问题是不能回头的,一个节点访问过了不能回来了,并不需要走完所有的路,但是中国邮递员问题可以多次访问一个节点,因为中国邮递员问题要求的是要访问所有的街道,即,每条街道必须访问到。
此问题是图遍历问题的一种。
无向图的中国邮路问题是容易解决的,是P问题;
有向图的中国邮路问题是NP完全问题。
欧拉回路
试想,假设每条路都走一次,最终恰好还能返回出发点,这样的拓扑图画出来应该满足怎样的结构呢?
每个节点要进去还要出去,所以,每个点的入度和出度必须相等(起始点也一样)。
每个节点的度应该是偶数个,满足这样的拓扑结构的图就是欧拉回路。
无向图的解决方法
G为欧拉图:
因为欧拉回路通过所有的边,因此任何一个欧拉回路即为此问题的解。
G的任意欧拉回路都是最优回路,从而可利用Floyd算法求解。
G不是欧拉图:
G的任意一个回路必定通过某些边不止一次。
其中必存在有奇数个边的端点,且这类的端点一定大于等于2个。
因此有些边需要再重复一次,使奇数边的端点变为偶数边的端点。
将边e的两个端点再用一条权为w(e)的新边连接时,称边e为重复的。
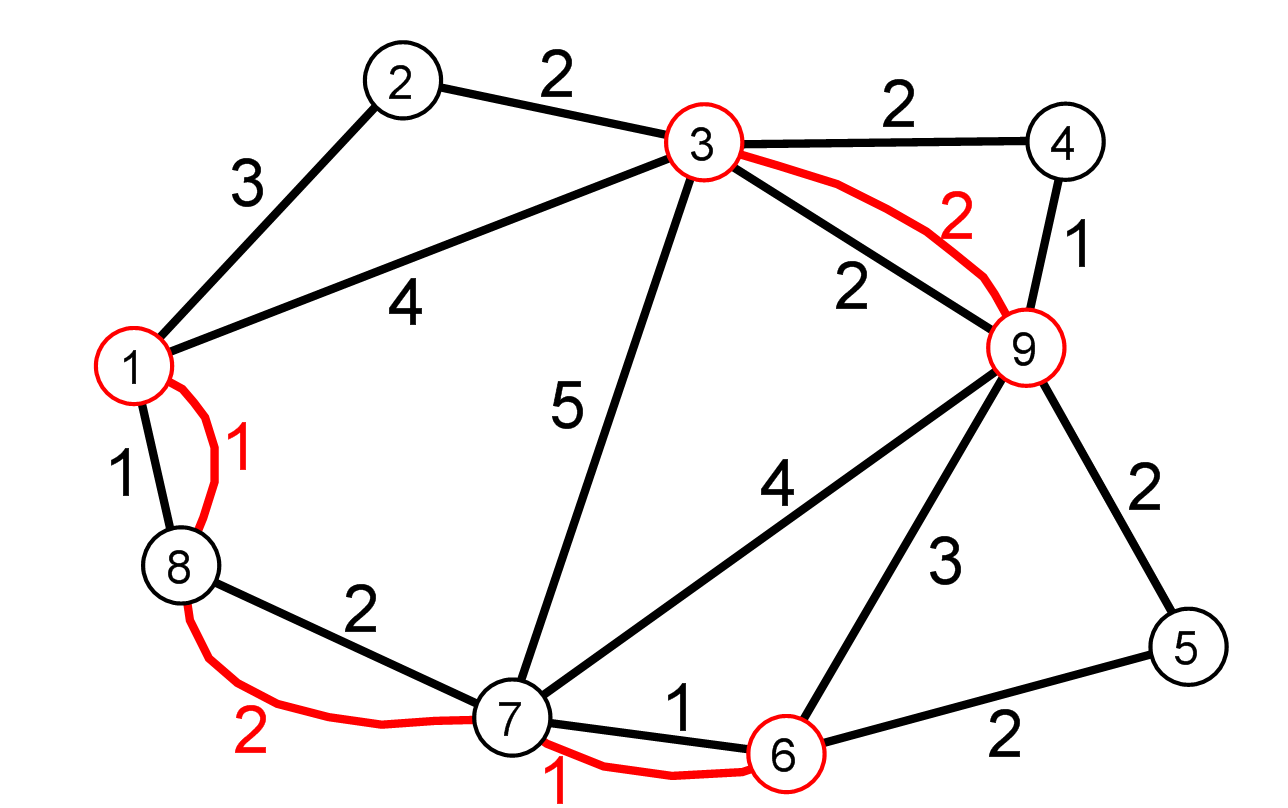
假设有一个镇有14条路及9个路口(路口分别编号为 1,2, …,9),其路和路口对应的图(右边第 1 图,边上的数字是各边的 cost)中有4个端点(编号 1, 3, 6 及9)有奇数个边通过,因此这个图不存在欧拉回路。
后续要作的在图中使几个边重复,使图中所有的端点均有偶数边通过。
例如若图中 {1,3} 及 {6.9} 边重复,所有的端点均有偶数边通过。不过增加的长度不一定最少。
为了要确定重复哪个边可以使原图的端点都有偶数边通过,且增加长度最少。
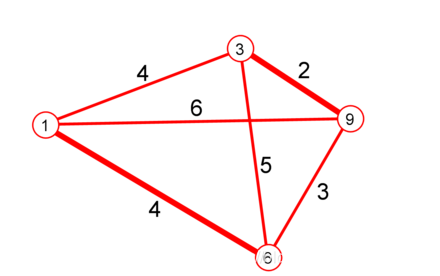
先画出所有奇数边的端点的完全图K4 ,边上的数字是从一端点到另一端点(可以经过其他完全图K4 中省略的点)的最短长度。
奇数度的点为1,3,6,9。 增加边使得奇数度的点变成偶数度,使得增加边的权重和最小。
若选择边 {1,6} 及 {3,9},所有端点都经过一次,而总长度4+2=6最短。
求的最短的路径,而原有的路径一定都是,所以,构造欧拉回路的边决定了最终的结果。
判断是否为欧拉回路,
如果是欧拉回路,直接相加返回结果,
如果不是欧拉回路,那存在奇数度的节点一定有偶数个。
(无向图所有顶点的度之和一定是偶数,且等于2倍的边数。因为握手定理,一条边两个度(出度入度)。)
1、根据统计每个节点度的数目,标记出奇数度的节点。
2、奇数节点一定是有偶数个,因此,最终的距离应该是:两两点之间的最短距离,而两两点之间的最短距离可以用Floyd或者Dijkstra或者bellman-ford算法来得到。
个人建议使用Floyd算法,不容易出错。
3、遍历所有的组合情况,求出最短的组合方式,
例如比较 d(2,8)+d(4,6),d(2,6)+d(4,8), d(2,4)+d(6,8),
然后取最小值即为最终的优化方案:d(2,8)+d(4,6)。
求解该步骤的时候,可以使用DFS来寻找最短路径方案,也可以利用DFS的思想,改为动态规划来实现
构造一个dp表,行值为1,列值表示该集合中所含的元素,
方案步骤:
1、生成邻接矩阵,利用Floyd算法求出每两个点之间的最短距离。(Floyd)
2、判断整个过程是否是欧拉回路,如果不是构造欧拉回路。
3、利用动态规划或者DFS计算构造欧拉回路的最优方案。
4、计算原路径与新构造路径的长度总和即为最终结果。
详细代码见 Floyd算法求最短路径问题