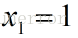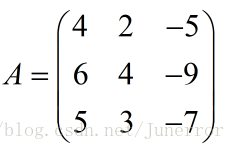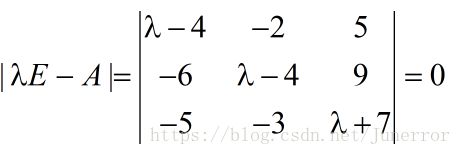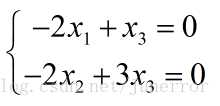一、一些术语
1、线性运算。
是加法和数量乘法, 在实数领域像只包含加法和数量乘法二元一次方程就属于线性运算,如y=3x+5。如果是矩阵的加法和数乘运算,就称为矩阵的线性运算;如果是向量的加法和数乘运算,统称为向量的线性运算。对于不同线性运算一般有不同的形式,它们满足交换律、结合律、分配律等。
二、向量
1、定义。
任取平面上两点,一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标。
2、数量积。
已知两个非零向量a、b,那么a·b=|a||b|cosθ(θ是a与b的夹角)叫做a与b的数量积或内积,记作a·b。零向量与任意向量的数量积为0。数量积a·b的几何意义是:a的长度|a|与b在a的方向上的投影|b|cos θ的乘积。两个向量的数量积等于它们对应坐标的乘积的和。即:若a=(x1,y1),b=(x2,y2),则a·b=x1·x2+y1·y2
3、向量积。
向量a与向量b的夹角:已知两个非零向量,过O点做向量OA=a,向量OB=b,则∠AOB=θ 叫做向量a与b的夹角,记作<a,b>。已知两个非零向量a、b,那么a×b叫做a与b的向量积或外积。向量积几何意义是以a和b为边的平行四边形面积,即S=|a×b|。
三、 矩阵(可以看作是向量)
1、转置。
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程称为矩阵的转置
2、乘法。
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵,它的一个元素:
并将此乘积记为:
例如:
3、行列式(如果是2介矩阵,就是平行四边形的面积)。
一个n×n的正方矩阵A的行列式记为或者
,一个2×2矩阵的行列式可表示如下 [13] :
一个n×n矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即:
代数余子式:在n阶行列式中,把元素aₒₑi所在的第o行和第e列划去后,留下来的n-1阶行列式叫做元素aₒₑi的余子式,记作Mₒₑ,将余子式Mₒₑ再乘以-1的o+e次幂记为Aₒₑ,Aₒₑ叫做元素aₒₑ的代数余子式。一个元素aₒₑi的代数余子式与该元素本身没什么关系,只与该元素的位置有关。
4、特征值和特征向量。
n×n的方块矩阵A的一个特征值和对应特征向量是满足的向量以及非零向量 [13] 。其中v为特征向量,
为特征值A的所有特征值的全体,叫做A的谱,记为
。矩阵的特征值和特征向量可以揭示线性变换的深层特性。式Ax=λx也可写成( A-λE)x=0,并且|λE-A|叫做A 的特征多项式。当特征多项式等于0的时候,称为A的特征方程,是一个齐次线性方程组,求解特征值的过程其实就是求解齐次线性方程组的解。其中
E:是单元矩阵,正对角线为1,其余为0的矩阵。
计算:A的特征值和特征向量。
得到特征值:、
因为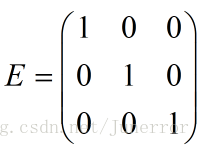
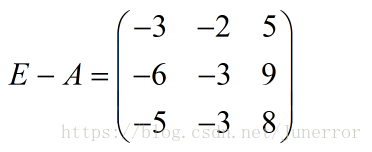
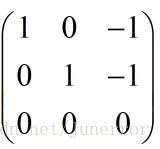
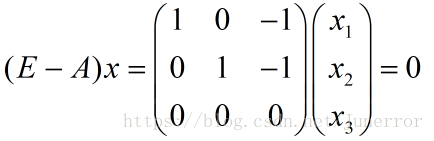
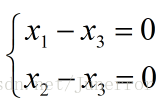
令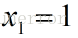
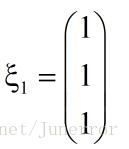
同理,当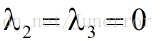
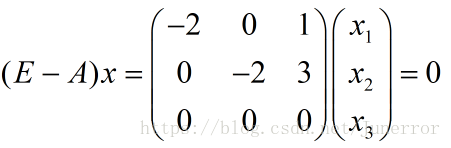
令