综述

　　线段树是一颗二叉搜索树，树的每一个节点均维护着区间信息，线段树根节点的区间信息可通过左子树和右子树的信息计算出（也就是我们说的满足区间加法）。

常见的几种区间加法：总的数字之和=左区间的数字和+右区间的数字和

　　　　　　　　　　总的gcd=gcd（左，右）

　　　　　　　　　　总的数字乘积=左区间乘积*右区间乘积

　　　　　　　　　　总的最大值=max(左区间最大值，右区间最大值）//最小值同理

　　它有什么用呢？它可以解决区间问题，可以在log(n)的时间进行单点查询，区间查询，单点修改等操作，例如题目给你一个长度为n的序列，要求进行k次操作，每次操作可能改动一个点的值，也可以查询区间L到R的和，如果单有查询那么可以用前缀和，加上修改前缀和就不行了，如果暴力做那么复杂度在查询就是O(nk)了，但如果用线段树可以优化到O(klogn)。

它长什么样？怎么存？

　　对于一颗维护长度为8的线段树，它的理念形态是长这样的：

　　总区间自然是1到8，那么左区间为什么是1到4右区间是5到8呢，因为线段树的核心是二分性质，区间【L，R】的左区间为【L，m】右区间为【m+1，R】，m为(L+R)/2。需注意端点m是属于左区间的。

　　那么如果赋予它实际的值，告诉你8个数字分别为1 2 3 4 5 6 7 8，那么它的实际情况是长这样的：

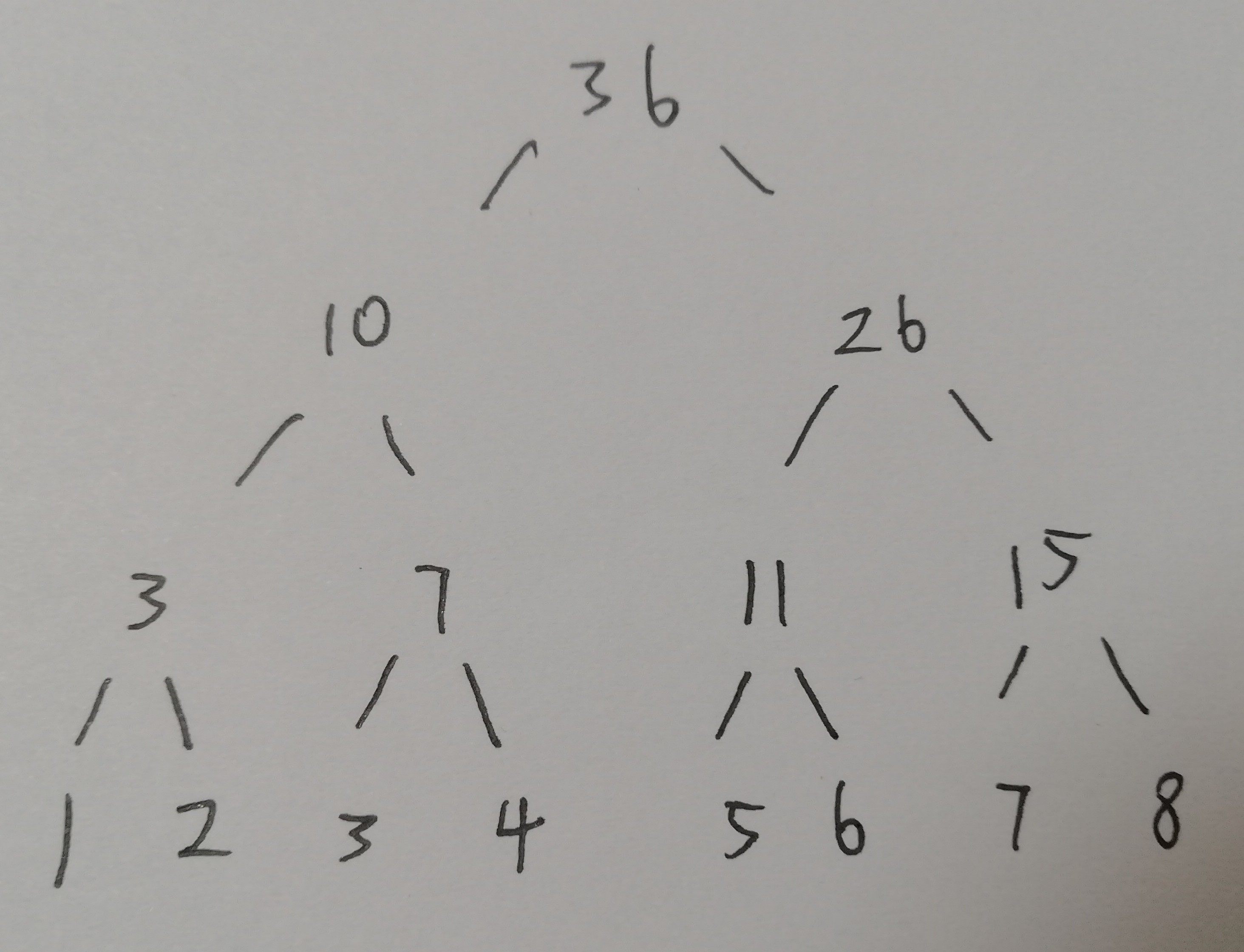
　　如果给它标号，每一层从上到下，从左到右由小到大进行标号，可以看得出来，根节点为n号时，左子树为2*n号，右子树为2*n+1号：

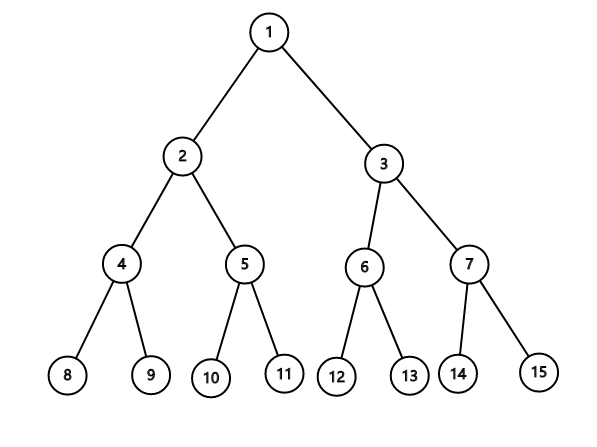
　　那怎么存呢？用数组来存，a[i]代表标号为i的节点信息，那么数组开多大呢？，数组的空间应该为节点的个数+1，那对于长度为n的线段树，节点有多少个呢？

　当n是2的幂时，那么线段树就是满二叉树，它的层数是log₂(n)+1，那么节点数就是2^层数-1也就是2n-1，当n不是2的幂的时候，线段树就会不那么好看，叶子节点的数组空间就不一定是连续的：

例如这个n=10的线段树：

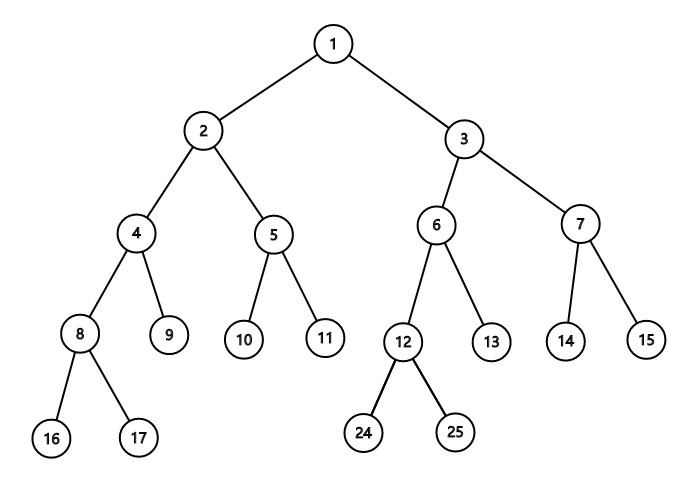
　　可以看到它不是满二叉数，满二叉树的n要达到16，若按照上面的计算公式开2n-1的空间数也就是19而已，而实际最大下标去到了25，不能满足，所以我们得开大一点，对于一个不是2的幂的n来说，我们令开多一层空间，就是是说n=10我们就开n=16的空间， n=17我们就开n=32的空间，log₂(n)+1是对于是2的幂的n的层数，为了方便无论n是不是2的幂，我们都开多一层空间给它，所以层数=log₂(n)+1+1 ，总节点数开到2^{log₂(n)+1+1}-1，也就是4n-1，所以开4倍就行，证毕！

普通线段树代码详解

　　要开的变量：maxn是n的最大范围，A[maxn]存题目的n个值的信息，对应线段树的叶子节点 a[4*maxn]是线段树的空间，节点的标号为i。

对于节点信息的维护

　　注意节点存的是什么信息，此代码存的是区间和：

void pushup(int rt){
    a[rt]=a[rt<<1]+a[rt<<1|1];
}

建树

　　建树的过程就是一直递归到叶子节点，然后把当前编号的空间赋值为对应题目的信息，在递归结束的时候要维护区间信息

 1 void build(int l,int r,int rt){//对于 l 到 r 的一颗线段树建树 
 2     if(l==r){//代表已经递归到叶子节点 
 3         a[rt]=A[l];
 4         return ;
 5     }
 6     int m=l+r>>1;
 7     build(l,m,rt<<1);//建左子树 
 8     build(m+1,r,rt<<1|1);//建右子树 
 9     pushup(rt);//左右子树建好之后维护当前区间的信息 
10 }

单点更新

　　单点更新其实就是一个找叶子节点编号的二分过程，当你找到对应叶子节点的位置，你想干嘛干嘛，这里是对应位置加上val值：

 1 void update(int pos,int val,int l,int r,int rt){//在pos位置加上val
 2     if(l==r){//代表已经递归到叶子节点 
 3         a[rt]+=val;
 4         return;
 5     }
 6     int m=l+r>>1;
 7     if(pos<=m)//目标位置在左边 
 8         update(pos,val,l,m,rt<<1);
 9     else//在右边 
10         update(pos,val,m+1,r,rt<<1|1);
11     pushup(rt);//更新完维护信息 
12 }

单点查询

　　单点查询其实和单点更新本质上相同，就是找到叶子节点，然后想干嘛干嘛

int search(int pos,int l,int r,int rt){
    if(l==r){
        return a[rt];
    }
    int m=l+r>>1;
    if(pos<=m)
        return search(pos,l,m,rt<<1);
    else
        return search(pos,m+1,r,rt<<1|1);
}

区间查询

　　在区间查询中，有两个区间，一个是查询区间我们设为【L，R】，一个是递归区间设为【l，r】。假如我们要查询区间和，设为ans。

 1 int query(int L,int R,int l,int r,int rt){
 2     if(L<=l&&r<=R){
 3         return a[rt];//第一种情况，直接贡献 
 4     }
 5     int m=l+r>>1;
 6     int ans=0;
 7     if(L<=m)//递归区间的左边含有查询 
 8         ans+=query(L,R,l,m,rt<<1);
 9     if(R>m)
10         ans+=query(L,R,m+1,r,rt<<1|1);
11     return ans;//统计二三情况的贡献，返回最终值 
12 }

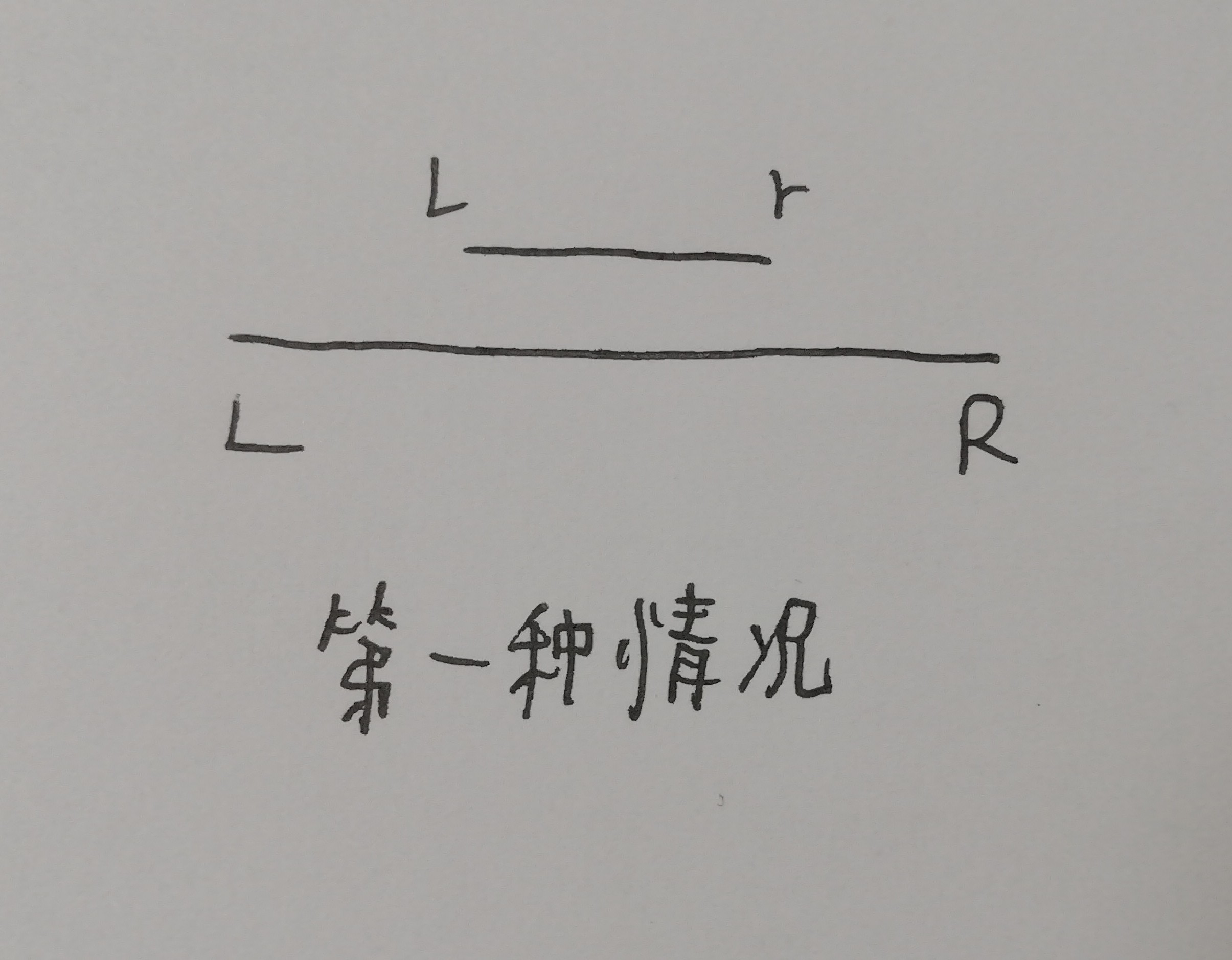
　　分三种情况:

　　一是递归区间属于查询区间，L<=l&&r<=R，就是说本节点所表示的信息你全部都要，那就贡献到ans里。

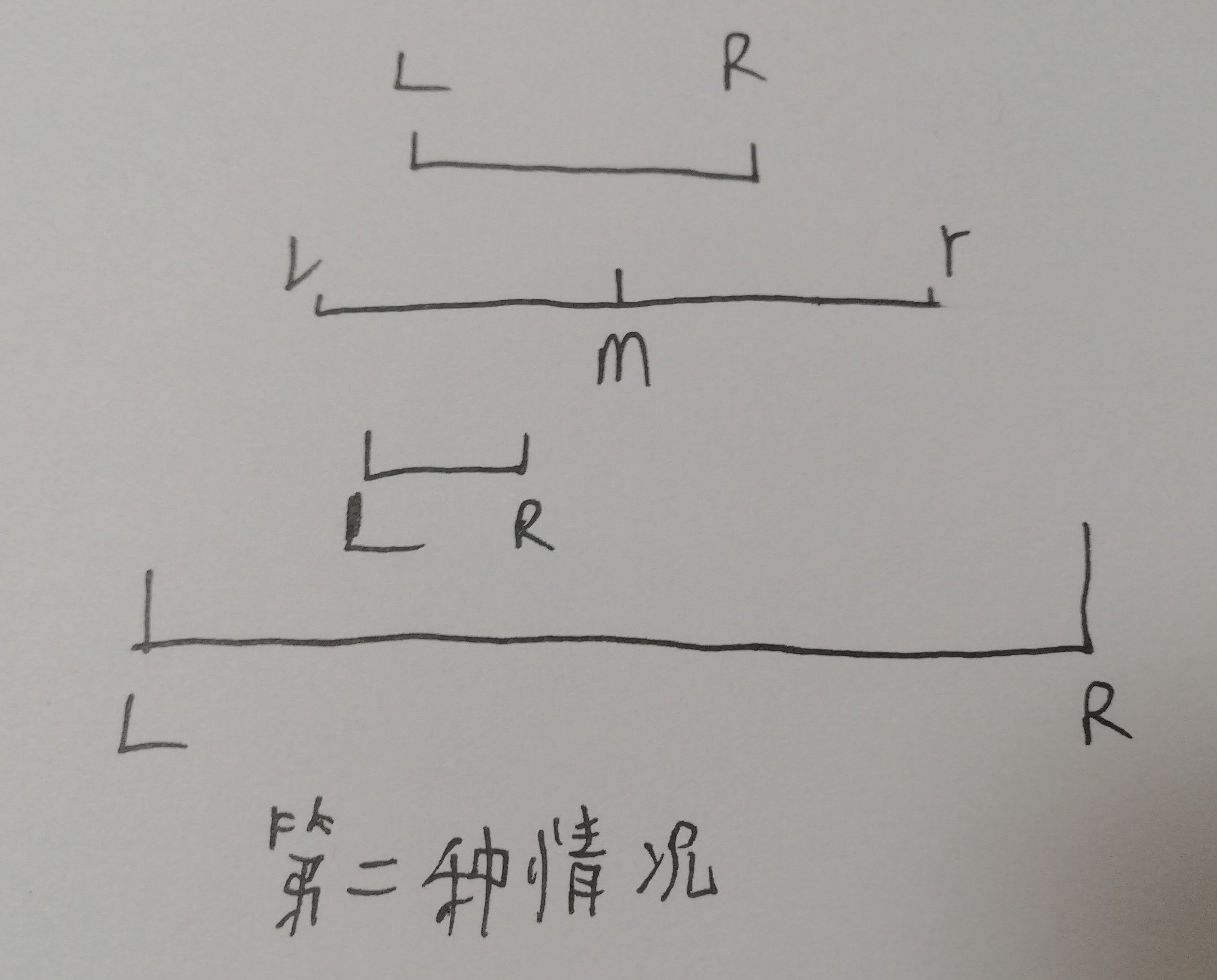
　　二是递归区间的左边有查询区间，L<=m,但本节点信息你不是全部要，得递归深一点，直到满足情况一才贡献ans，遂令下一个递归区间为【l,m】。

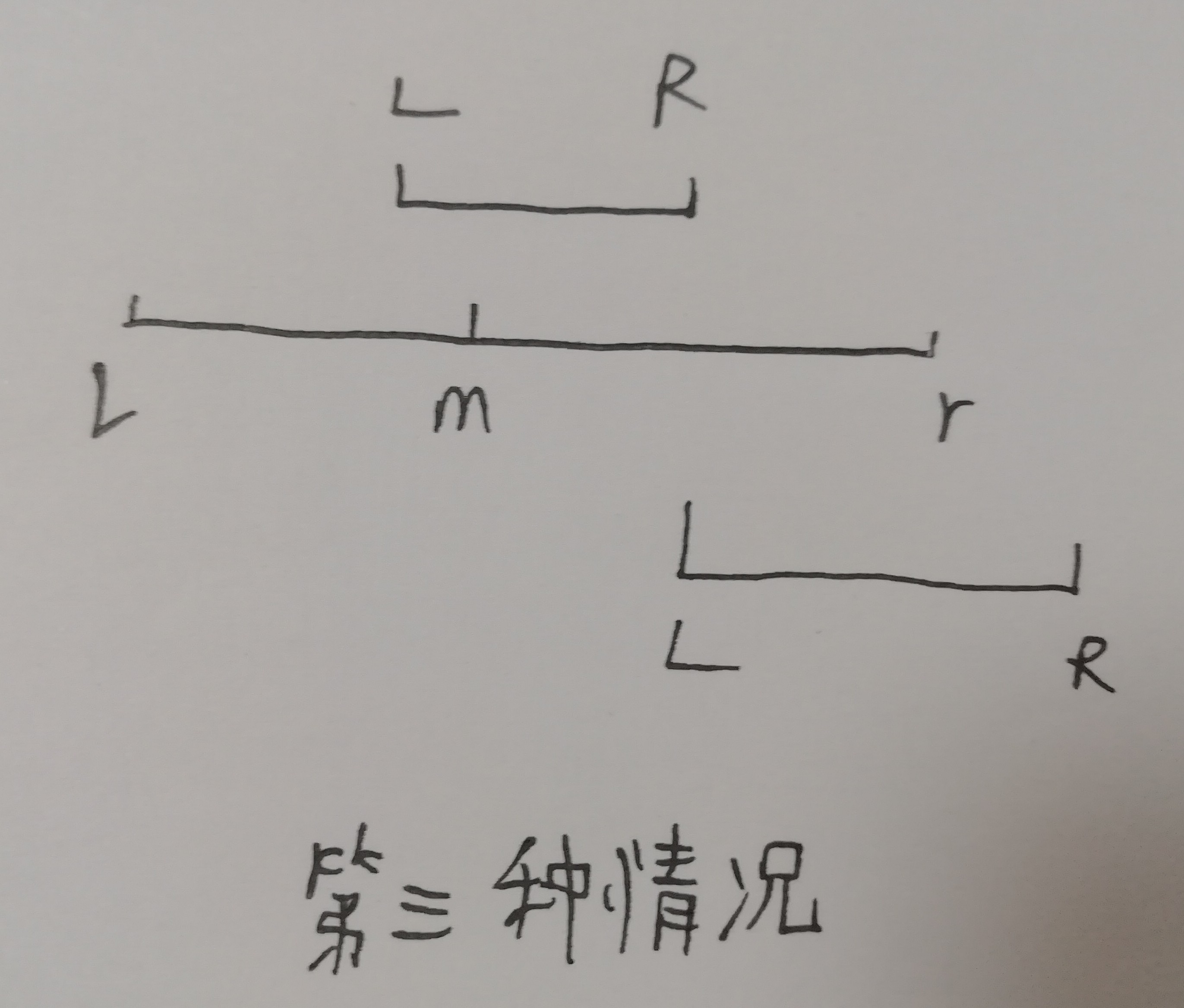
　　三是递归区间的右边有查询区间，R>m,但本节点信息你不是全部要，得递归深一点，直到满足情况一才贡献ans，遂令下一个递归区间为【R,m+1】。

区间更新

　　假如我们要将区间【L，R】中的每一个端点加上一个值val，如果区间更新用R-L+1个单点更新来做，那么复杂度要去到O(长度*logn)，那么最坏长度为整个序列那么长，就是nlogn了。为了降低时间复杂度，我们引入懒标记这一概念。

　　每一个节点都有一个懒标记值，懒标记——表示本节点的左右子树有区间更新需求但尚未更新。懒标记顾名思义就是太懒了，懒得递归下去，打个标记，之后如果要用到就顺便更新了。

　　举个例子，对于n=10，各个端点值为1 2 3 4 5 6 7 8 9 10，

segment tree 详解

综述