考虑一开始价值为1000美金的储蓄存单在月利率为1%的条件下的累计价值，下面的数列表示该储存单逐月的价值：
$A = (1000,1010,1020.10,....)$
我们对这个数列求差分，可以得到它的差分数列为：
$\Delta A = (10,10.10,10.20)$
我们可以很轻易的知道：
$\Delta a_i = a_{i+1}-a{i}=0.01*a_n$
有根据我们之前给出的式子:
$a_{i+1}=a_i+ \Delta a_i=a_{i}+0.01*a_i$
我们就得到了一个从当前项，转移到下一项的转移方程（我个人喜欢这么叫），最终我们得到了一个这样的动力系统模型：
$a_{i+1}=1.01*a_i , i=0,1,2,3,...$
$a_0 = 1000$
然后我们把代码一写，就可以把它变化的过程表示的清楚明了。我使用的是python，python在绘图方面的表现明显强于matlab，从另外一个角度来说，我用python用得顺手（逃）。

import matplotlib.pyplot as plt
A=[1000];#list A  , A[0] is 1000$
for i in range(100):# Calculat A[1],A[2],...,A[100]
    A.append(A[i]+A[i]*0.01);
plt.plot(range(101),A);#X is 0 --> 100 , Y is A[0] --> A[100]
plt.title(u"Bank deposits as a function of year", fontproperties='font')
plt.xlabel(u"year", fontproperties='font')
plt.ylabel(u"deposit", fontproperties='font')
plt.show();# Show the picture

我们可以得到以下关系
Alt
通过观察，我们知道，这个存款的上涨速度是不断地变快的，但是有生之年，还是涨不了多少。

那么，上面给出的方程：
$a_{i+1}=1.01*a_i , i=0,1,2,3,...$
$a_0 = 1000$
我们可以把它拆分成无数个代数方程，我们把它称为一个动力系统，我们可以看出，如果我们一致这个系统中的某一项，我们之恩那个紧接着算出来它的下一项，而不能直接算出特定项的值，所以我们需要进行迭代100次才能算出a₁₀₀的值。
如果我们每个月都要从账户中取走50块钱的话，我们就可以得到新的转移方程：
$\Delta a_i = a_i + 0.01*a_i -50$
我们稍微改一下自己的程序，就可以得到新的变化曲线，如下：
Alt

这时，经过我们的思考——不对啊!钱怎么能是负的呢！我们需要更改一下范围，再更改范围后，我们得到了新的图片:
Alt
这样就非常完美了，我们可以看出，23年后钱会被花光，准确的说是第23年取钱时，账户中不足50元。

一个序列就是定义域为全体非负整数集合上的一个函数，其值域为实数的一个子集，一个动力系统就是序列各项之间的一种关系，数值解就是满足该动力系统的一张数值表。

2、用差分法方程近似描述变化

上一个例子中，我们每个月的利息以及从银行中取走的钱都是固定的，我们的模型准确无比，完全贴合现实，但是现实是残酷的，我们的模型往往不能准确的描述客观世界，所以，我们需要画出现实世界的变化，观察模式，然后用数学术语来近似描述变化。
$change = \Delta a_n = afunction()$

离散变化与连续变化

很明显，在上一小节中，我们的存款每年只会发生一次变化，所以我们说，它的变化是在离散的时间区间上发生的。而正如我们所说，现实很残酷，很多的变化是连续地发生的，比如下面这个例子。

例1 酵母培养物的增长

下面表格中的数据是从测量酵母培养物增长的实验收集来的，图形显示可以假设种群量的变化和当前种群量的大小成比例。即： $\Delta$ p_n = p_n+1 - p_n = k*p,其中p_n表示n小时后种群生物量的多少，而k是一个正常数，k的值依赖于时间测量。

以小时计的时间_n	观察到的酵母生物量_ p_n	生物量的变化_p_n+1 - p _n
0	9.6	8.7
1	18.3	10.7
2	29.0	18.2
3	47.2	23.9
4	71.1	48.0
5	119.1	55.5
6	174.6	82.7
7	257.3	NULL

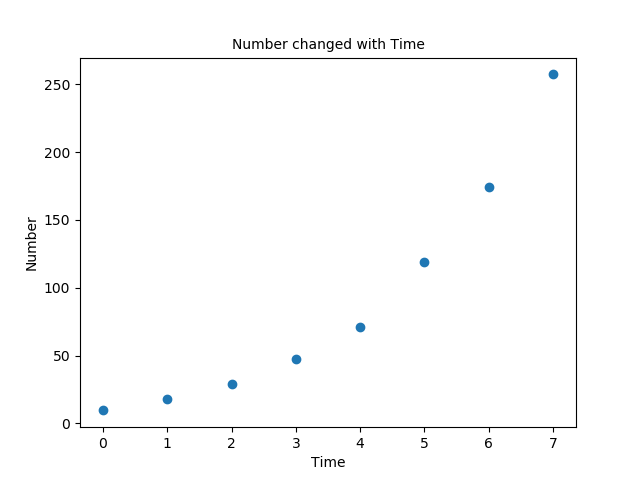
我们先把图画出来，以方便观察（我们以n为X轴，p_n为Y轴，进行绘图）

接下来我们再做出n与 $\Delta p_n$ 之间的关系图：

据书中所说，这个k我们的取值大约是在0.5左右，那么我们可以给出一个假设的比例模型：
$\Delta p_n = p_{n+1}-p_n=0.5*p_n$
我们得到了相邻两项之间的关系： $p_{n+1}=1.5*p_n$
但显然，这是不合理的。

模型存在的问题

食物、空间等资源只能支持某个最大限度的种群量而不能支持无限量的增长，当接近这个最大限度时，增长速度变慢。

例二进一步讨论酵母培养物的增长

我们得到了一张新的表格：

以小时计的时间_n	观察到的酵母生物量_ p_n	生物量的变化_p_n+1 - p _n
0	9.6	8.7
1	18.3	10.7
2	29.0	18.2
3	47.2	23.9
4	71.1	48.0
5	119.1	55.5
6	174.6	82.7
7	257.3	93.4
8	350.7	90.3
9	441.0	72.3
10	513.3	46.4
11	559.7	35.1
12	594.8	34.6
13	629.4	11.4
14	640.8	10.3
15	651.1	4.8
16	655.9	3.7
17	659.6	2.2
18	661.8	NULL

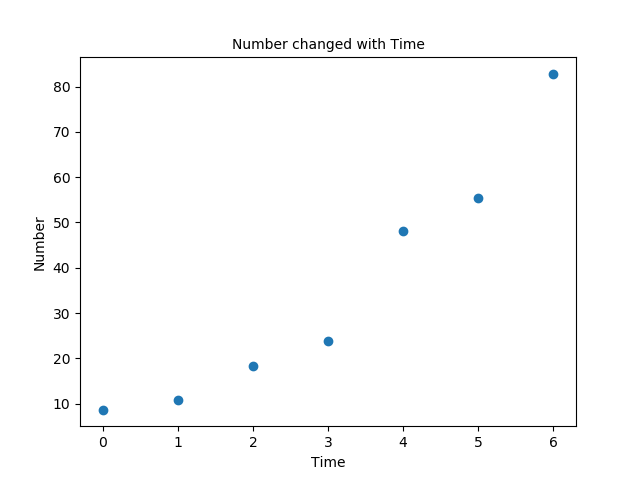
我们还是和刚才一样，把图给他画出来：

我们可以看到，随着时间的增多，微生物的增长趋势逐渐放缓，而且根据图形，我们可以估计出，我们的容纳量是在665左右[因为超过665后，增速很快的降低了]（这可能是因为，在达到容纳量后培养基所提供的营养物质、以及培养皿所提供的空间，都不适宜该微生物的生存了），在知道样本容纳量后我们可以使用这样的模型：
$\Delta p_n = p_{n+1}-p_n = k(Capacity - p_n )*p_n$
其中Capacity代表容纳量，在这个模型中，有：
$Capacity = 665$
这样构建出的模型，随着p_n的增长，变化 $\Delta p$ 逐渐减小
我们可以画出一个(665 - p_n)*p_n与 $\Delta p$ 之间的关系图：

观察到这里，我女朋友找我视频了，我视频完再慢慢写嘿嘿嘿。

好了，视频完了，开始继续写。

我们可以近似地求出，斜率k与等于 0.00082，所以我们可以给出模型：
$p_{n+1}-p_n=0.00082*(665-p_n)*p_n$
通过移项，我们可以得到：
$p_{n+1}=p_n+0.00082*(665-p_n)*p_n$
该方程是二次的，这种动力系统是非线性的，而且一般不能球的解析解，也就是讲，一般不能求得用n来表示的解析解，只能迭代的进行求解，下面我们根据我们的模型来进行预测：
假设我们已知p₀ = 9.6 那么我们可以进行预测：

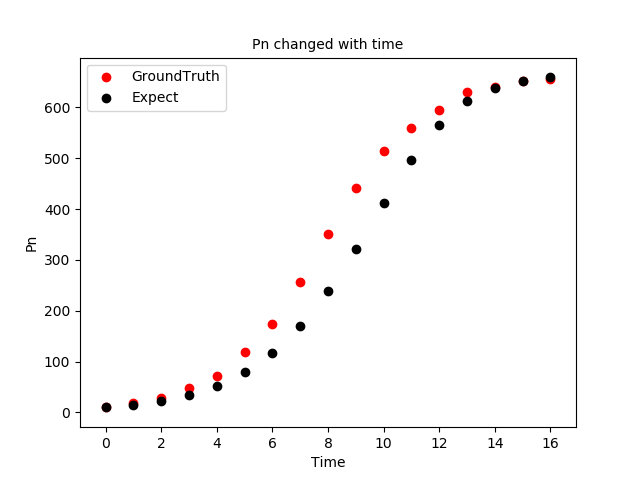
如图中所示，红色的点代表实际情况中的点，而黑色的代表我们预测的值，我们可以看出，虽然中间一段没对上，但是我们的模型已经将它变化的趋势表现得淋漓尽致了。

小结

书上除了这两个例题之外还给出了三个其他例题，在此就不多枚举了。总体来说，当我们发现我们解决的问题的曲线大致是一个S型曲线的时候，就可以使用这种模型进行解决。而且除了这种非线性的，我们也可以构建一个像是 $p_{n+1}=p_n+k(Capacity-p_n)$ 这样的模型.一切根据实际情况而判断.

3、动力系统的解法

猜测法（抄书）

猜测法是强有力的数学方法，先假设动力系统的解的形式，然后再去判断假设是否合理，这种方法要基于探索和观察并据此摸清解的模式，下面我们从一个例子开始。

再论储蓄存单

我们在第一节中讲过储蓄存单的问题，在初始时我们有1000美元，每年有1%的利息，如果既不存款也不付款，那么我们会有如下的动力系统：
$a_{n+1}=1.01*a_n$
$a_0=1000$
很显然，这个数列是无限增长的，而且我们可以说，这个数列的第k项
$a_k=1000*(1.01)^k$ ，emmm，所以我们就可以说，这个动力系统的解为:
$a_k=1000*(1.01)^k ,k=1,2,3,...$

总体的讲，猜测法可以分为以下几个步骤：

观察模式
猜测动力系统解的形式（个人认为这个是最重要的）
用代入法来测试该猜测（我们上面没有写这个部分）
接受或拒绝该猜测取决于再代入和代数运算后结构是否满足该动力系统，为了接受该猜测，带入的结果必须是恒等式

模型一：线性动力系统 $a_{n+1}=r*a_n$

这个线性动力系统就像是我们上面说的这个例子中的一样，总体有：
$a_0=a$
$a_{n+1}=r*a_n$
这个非常简单，我们就不多讲述。

模型一再讨论： $a_{n+1}=r*a_n$ 的长期行为

在这里我们对r进行分类讨论，根据他们的不同图像，来讨论动力系统的长期行为。

$r>0$ 的情况：

$r>1$ 时 $a_n$ 的取值无界，很简单，不谈了
$r<1$ 时 $a_n$ 的取值逐渐趋向于0，也很简单
$r<1$ 时 $a_n$ 的取值不变，更简单

$r<0时：$

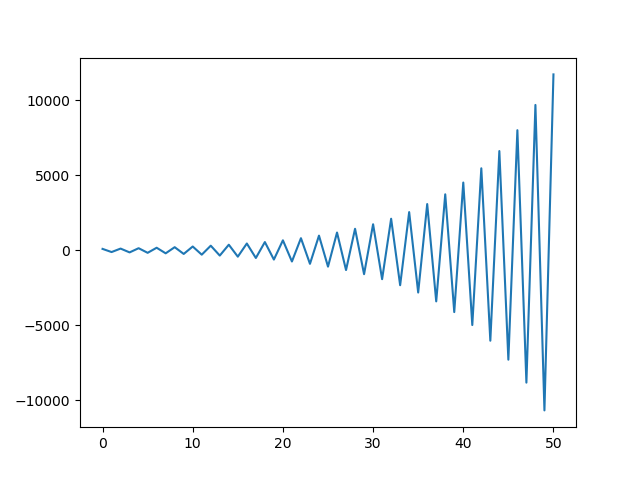
当 $r<-1$ 时，我们假定 $a_0=100$ ， $r=-1.1$ 可以画出这样的图像:
为了实现这个功能，我们可以用python写一个简单的迭代就可以了：

import matplotlib.pyplot as plt
X=[0];
Y=[100];
for i in range (50):
    X.append(i+1);
    Y.append(Y[i]*(-1.1));
plt.plot(X,Y);
plt.show();

可以看出我们的图像震荡幅度越来越大，我们称之为震荡增长的
*当 $r>-1$ 时，我们假定 $a_0=100$ ， $r=-0.9$ 可以画出这样的图像:
可以看出我们的图像震荡幅度越来越小，我们称之为震荡衰减的

$a_{n+1}=r*a_n+b$ 动力系统，r，b为常数

定义当 $a_0=a$ 时,如果对所有的 $k=1,2,3,...$ 有 $a_k=a$ ,则将数a成为动力系统 $f(a_n)$ 的平衡点或不动点，即 $a_k=a$ 是该动力系统的常数解

求平衡点并对其进行分类

我们已知动力系统满足下式：
$a_0 = a$
$a_{n+1}=r*a{n}+b$
又因为该动力系统是平衡的，所以有:
$a_{n+1}=a_n=a_0=a$
所以我们可以知道:
$a=r*a+b$
通过简单的运算，可以得到:
$a=\frac{b}{1-r}, if (r \not= 1)$
所以说， $a = \frac{b}{1-r}$ 为该系统的平衡点

而对于某个(依赖初始条件的)常数c，动力系统 $a_{n+1}=r*a_n+b,r \not =1$ 的解为：
$a_k=r^k*c+\frac{b}{1-r}$

非线性方程组

回想一下我们之前写过的一个式子：
$p_{n+1}=p_n=0.00082(665-p_n)$
我们经过一系列的代数运算后可以把它化简为一个这样的式子:
$a_{n+1}=r*(1-a_n)*a_n$
在这个动力系统中，r非常小的变化会引起解行为发生巨大的变化，像是 $a_0=0.1,r=3.750$ 时,我们编写程序:

import matplotlib.plot as plt
X=[0];
Y=[0.1];
for i in range(100):
	Y.append(3.75*(1-Y[i])*Y[i]);
	X.append(i+1);
plt.scatter(X,Y);
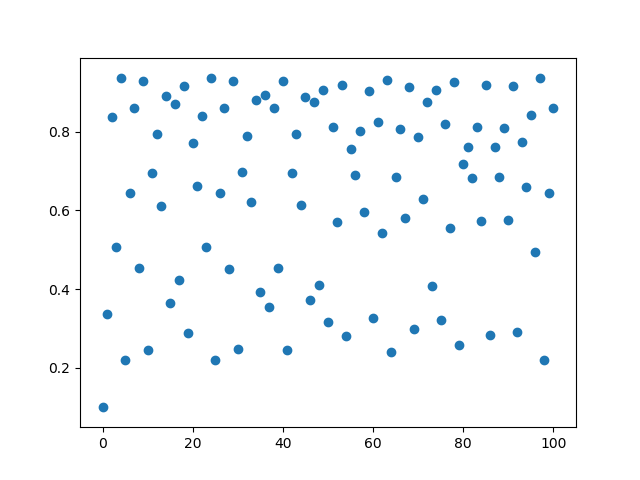
plt.show();

会发现，现在的系统发生了巨大的变化，我们上图中所展示出的行为称为混沌行文，混沌系统展示了他们对系统的常数参数的敏感性，给定的混沌系统对初始条件可以十分敏感。

4、差分方程组

在本节中，我们研究差分方程组，对于所选择的起始值，建立数值解以求当差该系统的长期行为。在第三节中我们知道，平衡点是一种取值，一旦到达了平衡点，系统就不会再有变化了。本节中，我们要求出平衡点，然后对平衡点附近的起始值进行探究，如果从靠近一个平衡点的起始值开始，我们想知道该系统是否：

仍然靠近该平衡点
趋近该平衡点
不再靠近该平衡点
再平衡点附近会发生什么将提供有关该动力系统长期行为的洞察，该动力系统展示周期行为么？有震荡行为么？由数值解描述的长期行为对初始条件、所研究的行为的建模中用到的比例常数的微小变化敏感么？

例1 汽车租赁公司

一家汽车租赁公司在奥兰多和坦帕都有分公司，这家公司是专门为满足在这两个城市开展旅游活动的旅行社的需要而开设的，因此，游客可以在一个城市租车而在另一个城市还车，游客可能在两个城市都有旅行计划。该公司想确定对这种方便的接换车方式的收费应该为多少。因为汽车可以在两个城市归还，每个城市就要有足够的车辆以满足用车需要，如果置放的车辆不够了，那么要从奥兰多运送多少车辆到坦帕运送多少车辆到奥兰多呢？对这些问题的回答将有助于该公司计算出它的期望成本。
历史数据揭示：约有60%在奥兰多出租的车辆还到了奥兰多，另外40%的车辆还到了坦帕。在坦帕分公司出租的车中，有70%仍旧还到了坦帕，另外30%的车辆还到了奥兰多。

动力系统模型 我们来研究该系统的一个模型，令n表示营业天数，有定义：
$O_n = 第n天营业结束时在奥兰多的车辆数$
$T_n = 第n天营业结束时在坦帕的车辆数$
因此历史记录显示该系统应该是
$O_{n+1}=0.6*O_n+0.3*T_n$
$T_{n+1}=0.4*O_n+0.7*T_n$
平衡点 该系统的平衡点就是是系统不再发生变化的O_n和T_n的值。如果它们存在的话，分别称为平衡点O和T，同时有 $O=O_{n+1}=O_n$ 和 $T=T_{n+1}=T_n$ ，带入我们的模型，我们可以得到以下的方程：
$O=0.6*O+0.3*T$
$T=0.4*O+0.7*T$
$\left[ \begin{matrix} -0.4& 0.3\\ 0.4&-0.3 \end{matrix} \right] * \left[ \begin{matrix} O\\T \end{matrix} \right] = \left[ \begin{matrix} 0\\0 \end{matrix} \right]$
我们解这个方程组可以得到， $O=\frac{3}{4}T$ ，如果该公司有7000辆车，而且开始时在奥兰多有3000辆车而在坦帕有4000辆车，那么我们的模型预测：
$O_1=0.6*3000+0.3*4000=3000$
$T_1=0.4*3000+0.7*4000=4000$
因此如果该系统在 $(O,T)=(3000,4000)$ 处开始，将保持不变

接下来我们探究如果从不同于平衡点的值开始会怎么样，我们对以下四个初始条件来迭代该系统：

序号	奥兰多	坦帕
1	7000	0
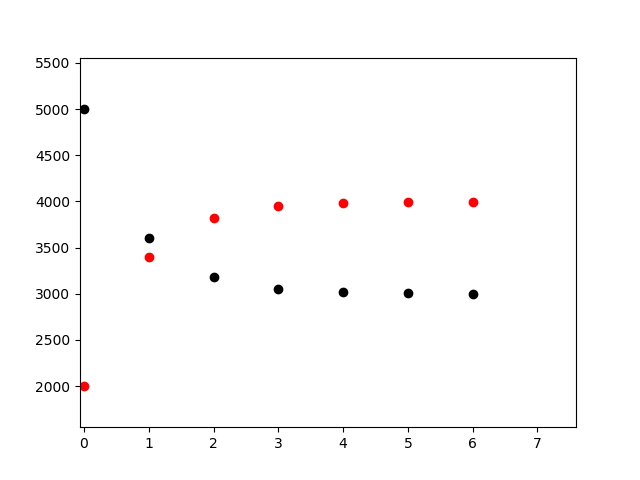
2	5000	2000
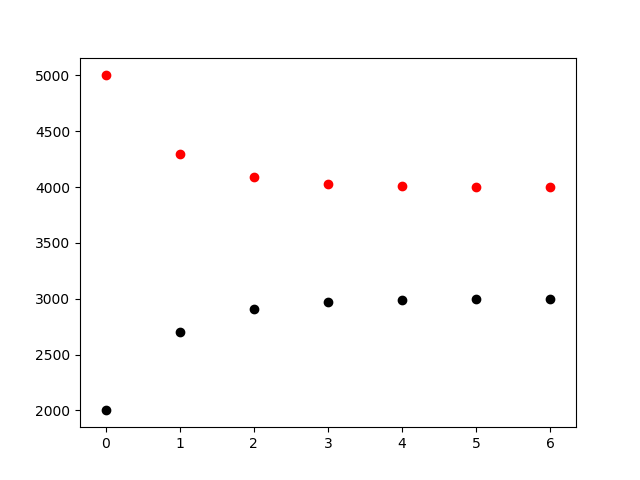
3	2000	5000
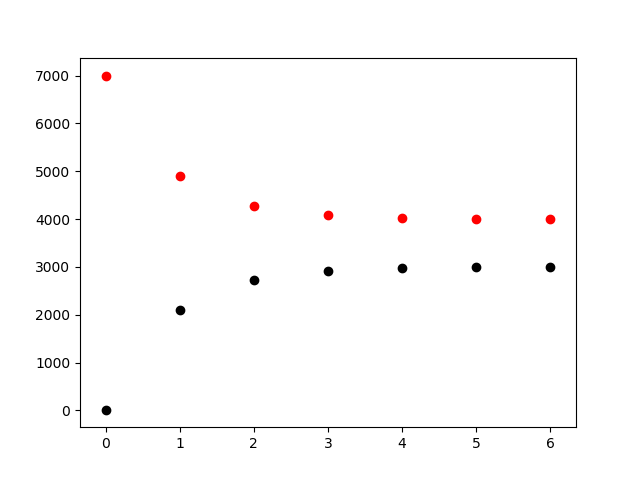
4	0	7000

接下来我们编程，将图像画出
以下四张图片对应序号从1到4的情况：

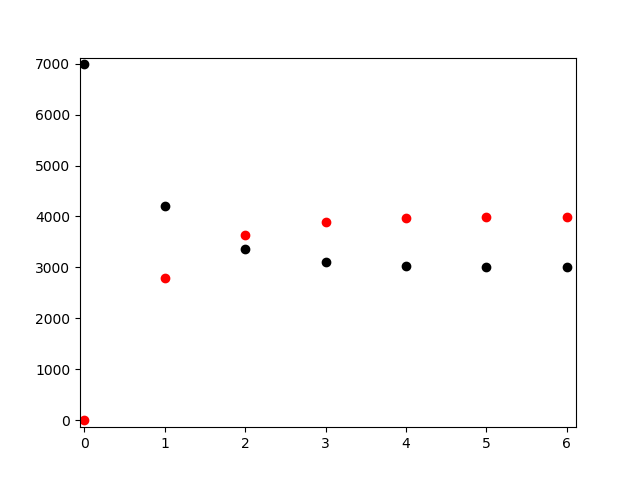
对初始条件的敏感性以及长期行为 四种情况中的每一种情况在第一周内都是和平衡点很接近的，甚至在其中一个城市没有车的情况下也是如此，结果暗示平衡点是稳定的而且对起始值不敏感的。

我是赛赛

发布了21 篇原创文章 · 获赞 8 · 访问量 718

私信关注

《数学建模》笔记（一）—— 第一章对变化进行建模

《数学建模》笔记（一）—— 第一章对变化进行建模

个人简介

0 、预备知识

比例性

对变化进行建模

1、 用差分方程对变化进行建模

1.1 对于一个数列 A = {a0,a1,a2,…} 它的一阶差分是：

1.2 经典问题

2、用差分法方程近似描述变化

离散变化与连续变化

例1 酵母培养物的增长

模型存在的问题

例二 进一步讨论酵母培养物的增长

小结

3、动力系统的解法

猜测法（抄书）

再论储蓄存单

模型一：线性动力系统 a n + 1 = r ∗ a n a_{n+1}=r*a_n an+1​=r∗an​

模型一再讨论： a n + 1 = r ∗ a n a_{n+1}=r*a_n an+1​=r∗an​的长期行为

a n + 1 = r ∗ a n + b a_{n+1}=r*a_n+b an+1​=r∗an​+b动力系统，r，b为常数