本文仅作为《算法》第四版图的相关知识的个人笔记。
几个概念:
1.连通图:
从任意一个顶点都存在一条路径到达另一个任意顶点。非连通图由若干连通图组成,都是极大连通子图。
2.树是一个无环连通图。连通图的生成树是其一个子图,拥有图的所有顶点。
3.二分图
一种能够将所有节点分为两部分的图。简单的说,如果按双色上色,二分图的任意两个相邻的顶点的颜色不同。
4. 两个顶点通过一条边连接,称为相邻的。顶点的度数为与他相连的边的总数。有向图中的度数分为入度和出度,入度为指向该顶点的边的总数,出度为从该顶点指出的边的总数。
5. 自环:一条连接顶点和其自身的边
6. 一对顶点的两条边称为平行边。
PartOne:无向图相关算法
一、无向图
1.1 数据结构
/**
* 顶点数目
*/
private final int V;
/**
* 边的数目
*/
private int E;
/**
* 邻接表,Bag为背包,为一个只入不出的队列,adj[v]即表示与顶点v相连的顶点,因此相邻的两个顶点v和w分别会出现在对方的邻接表中
*/
private Bag<Integer>[] adj;
1.2 构造
public Graph(int v) {
V = v;
this.E=0;
adj=new Bag[V];
for (int i = 0; i < V; i++) {
adj[i]=new Bag<>();
}
}
1.3 相关方法
两顶点是否相邻:
public boolean hasEdge(int v,int w){
//遍历顶点v的邻接表,查找有无顶点w
for(int x:adj(v)){
if (x==w){
return true;
}
}
return false;
}
添加一条边:
public void addEdge(int v,int w){
//也可以通过判断v==w和hasEdge(v,w)决定是否允许自环和平行边
adj[v].add(w);
adj[w].add(v);
E++;
}
//顶点度数
public int degree(int v){
int degree=0;
for (int w:adj(v)){
degree++;
}
return degree;
}
//最大度数
public int maxDegree(){
int max=0;
for (int v = 0; v < V; v++) {
int degree = degree(v);
if (degree>max){
max=degree;
}
}
return max;
}
//自环数
public int numOfSelfLoops(Graph graph){
int loops=0;
for (int i = 0; i < graph.V(); i++) {
for(int w:graph.adj(i)){
if (w==i){
loops++;
}
}
}
return loops/2;
}
二、深度优先搜索
简单的说就是 从给定顶点出发,一直向下走,直到下面没有路了,然后返回上一个顶点,继续进行同样方式遍历,直到遍历完所有的顶点。
因此我们需要如下的数据结构:
/**
* 标记顶点i是否被访问
*/
private boolean[] marked;
/**
* 从起点到一个顶点的已知路径上的最后一个顶点
* 如 v->w->x 则edgeTo[w]=v,edgeTo[x]=w
*/
private int[] edgeTo;
/**
* 遍历的起点
*/
private final int s;
构造函数:
public DepthFirstPaths(Graph G, int s) {
this.s = s;
//初始化两个数组
edgeTo = new int[G.V()];
marked = new boolean[G.V()];
dfs(G, s);
}
深度优先遍历:
private void dfs(Graph G, int v) {
//标记当前顶点为true
marked[v] = true;
//遍历与当前顶点相邻的顶点
for (int w : G.adj(v)) {
//如果没有被访问
if (!marked[w]) {
//标记起点到当前顶点的最后一个路径
edgeTo[w] = v;
//从当前节点继续进行遍历
dfs(G, w);
}
}
}
是否存在从起点到指定顶点的路径:
public boolean hasPathTo(int v) {
validateVertex(v);
return marked[v];
}
返回从起点到指定顶点的路径,如果不存在返回null:
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)){
//没有到达路径,返回null
return null;
}
//因为edgeTo保存的是到达当前节点的父节点,因此使用栈结构,这样从当前节点到起始顶点的顶点依此入栈,遍历的时候便是从起点到该顶点的完整路径
Stack paths=new Stack();
for (int i = v; i !=s ; i=edgeTo[i]) {
paths.push(i);
}
paths.push(s);
return paths;
}
测试:
public static void main(String[] args) {
Graph graph=new Graph(6);
graph.addEdge(0,2);
graph.addEdge(0,1);
graph.addEdge(0,5);
graph.addEdge(2,1);
graph.addEdge(2,3);
graph.addEdge(2,4);
graph.addEdge(3,5);
graph.addEdge(3,4);
DepthFirstPaths dfs=new DepthFirstPaths(graph,0);
Iterable<Integer> paths = dfs.pathTo(4);
for (Integer i:paths){
System.out.println(i.toString());
}
}
结果:
0
5
3
4
三、广度优先搜索:
广度优先搜索的思想是,从当前节点,先遍历与该节点相邻的所有节点,然后再对相邻顶点进行广度优先遍历。
深度优先是纵向遍历,广度优先是横向遍历。
数据结构:
广度优先搜索的数据结构同深度基本一样:
public class BreadthFirstPaths {
private final int start;
private int[] edgeTo;
private boolean[] marked;
public BreadthFirstPaths(Graph graph,int start) {
this.start = start;
edgeTo=new int[graph.V()];
marked=new boolean[graph.V()];
bfs(graph,start);
}
}
但在遍历的时候采用队列进行辅助,思想如下:
1.将当前顶点加入队列
2.从出队出队一个顶点(第一次时出队的就是当前节点),遍历该顶点的所有相邻顶点,置marked[v]为true,并依此入队。
3.当队列非空时,循环步骤2
代码如下:
private void bfs(Graph graph, int start) {
Queue<Integer> queue=new Queue<>();
queue.enqueue(start);
marked[start]=true;
while (!queue.isEmpty()){
int v = queue.dequeue();
for (int w:graph.adj(v)){
queue.enqueue(w);
edgeTo[w]=v;
marked[w]=true;
}
}
}
四、连通分量
数据结构如下:
public class CC {
private boolean[] marked;
/**
* 顶点属于哪个连通分量 如 顶点v属于第count个连通分量,则id[v]=count
*/
private int[] id;
/**
* 第count个连通分量的顶点数
*/
private int[] size;
/**
* 连通分量数
*/
private int count;
}
思想如下:
遍历所有的顶点,对每个顶点都执行dfs深度优先遍历,如果两个顶点在同一个连通分量,那么在对一个顶点进行dfs遍历的时候,两个顶点必然会在构造函数的一个dfs中被访问到,属于同一个连通分量。
构造函数:
public CC(Graph G) {
marked = new boolean[G.V()];
id = new int[G.V()];
size = new int[G.V()];
//代码1
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
dfs(G, v);
//与顶点v连通的所有顶点都遍历完毕后,说明该连通分量所有顶点已遍历完毕,增加count
count++;
}
}
}
private void dfs(Graph G, int v) {
marked[v] = true;
//顶点v属于第count个分量
id[v] = count;
//第count个分量的顶点数加1
size[count]++;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
}
五、判断是否为无环图
对于无向图而言,判断其是否为无环图很简单,在对某个顶点进行dfs遍历时,假如它的相邻顶点已被访问过,那么有两种可能:
以
3-4-5-3为例
每次dfs都传递要遍历的节点,和当前刚刚被遍历过的节点
一开始三个顶点都未被访问
1.现在对3进行dfs,访问到5,5被标记为true;
2.再对5进行dfs,此时3已经被访问,但是此时的3属于顶点5的父级,不构成环,再访问4,标记4为true;
3.接着对4进行dfs,此时顶点5被访问,同2一样,顶点5属于顶点4的“父级”,不构成环,但是3也被访问了,且3不是顶点4的“父级”,因此此处出现环。
关键代码如下:
private boolean[] marked;
private boolean hasCycle;
public Cycle(Graph G) {
marked=new boolean[G.V()];
for (int i = 0; i < G.V(); i++) {
if (!marked[i]){
dfs(G,i,i);
}
}
}
private void dfs(Graph G,int v, int u){
marked[v]=true;
for(int w:G.adj(v)){
if (!marked[w]){
dfs(G,w,v);
}else if (w!=u){//如 3:5 5:3 就不构成环
hasCycle=true;
}
}
}
六、二分图问题
这个同无环图问题类型,在对一个顶点进行dfs遍历时,将其未被访问的临接顶点置为与该顶点对立的颜色,若已经被访问,则判断该顶点的颜色与当前顶点的颜色是否不一样,如果一样,则不是二分图。
关键代码如下:
private void dfs(Graph graph, int v) {
marked[v]=true;
for (int w: graph.adj(v)){
if (!marked[w]){
color[w]=!color[v];
dfs(graph,w);
}else if (color[w]==color[v]){
isTwoColorable=false;
break;
}
}
}
PartTwo:有向图相关算法
有向图的定义和无向图基本一样,这里也是基于临接表实现,但在插入边的时候,有向图只需要操作边的始点的邻接表,不需像无向图一样两个顶点的邻接表都插入对应的顶点。
public class Digraph {
private final int V;
private int E;
private Bag<Integer>[] adj;
public Digraph(int v) {
V = v;
this.E=0;
adj=new Bag[V];
for (int i = 0; i < v; i++) {
adj[i]=new Bag<>();
}
}
public int V(){
return V;
}
public int E(){
return E;
}
public void addEdge(int v,int w){
adj[v].add(w);
E++;
}
public Iterable<Integer> adj(int v){
return adj[v];
}
/**
* 获取当前有向图的反转图
*/
public Digraph reverse(){
Digraph R=new Digraph(V);
for (int v = 0; v < V; v++) {
for (int w: adj(v)){
R.addEdge(w,v);
}
}
return R;
}
}
一、有向图的可达性:
这里同无向图一样,只需将Graph换为Digraph即可:
进行DFS遍历:
public class DirectedDFS {
private boolean[] marked;
/**
* 单点可达性
* 经过此方法,从marked(int v)返回是否存在一条从s到达给定顶点v的有向路径
* @param digraph
* @param s
*/
public DirectedDFS(Digraph digraph,int s) {
marked=new boolean[digraph.V()];
dfs(digraph,s);
}
/**
* 多点可达性
* 是否存在一条从集合中的任意顶点到达给定顶点v的有向路径
* @param digraph
* @param sources
*/
public DirectedDFS(Digraph digraph,Iterable<Integer> sources) {
marked=new boolean[digraph.V()];
for (int s:sources){
if (!marked[s]){
dfs(digraph,s);
}
}
}
private void dfs(Digraph digraph, int v) {
marked[v]=true;
for (int w:digraph.adj(v)){
if (!marked[w]){
dfs(digraph,w);
}
}
}
public boolean marked(int v){
return marked[v];
}
public static void main(String[] args) {
Digraph graph=new Digraph(6);
graph.addEdge(0,2);
graph.addEdge(0,1);
graph.addEdge(0,5);
graph.addEdge(2,1);
graph.addEdge(2,3);
graph.addEdge(4,5);
DirectedDFS dfs=new DirectedDFS(graph,0);
System.out.println(dfs.marked(3));
}
}
顶点对的可达性
借助DirectedDFS数组,我们可以实现顶点对的可达性:
无论对于稀疏还是稠密的图,它都是理想的解决方案,但不适用于实际应用中的大型有向图,因为构造函数所需的空间和V²成正比,所需时间和V(V+E)成正比
public class TransitiveClosure {
private DirectedDFS[] directedDFS; // tc[v] = reachable from v
/**
* 构造函数
* 所需空间与V²成正比
* 所需时间与 V(V+E)成正比
* @param G
*/
public TransitiveClosure(Digraph G) {
directedDFS = new DirectedDFS[G.V()];
for (int v = 0; v < G.V(); v++)
directedDFS[v] = new DirectedDFS(G, v);
}
boolean reachable(int v,int w){
return directedDFS[v].marked(w);
}
}
二、单点有向路径和单点最短有向路径
同无向图一样,单点有向路径就是借助DFS,对从s到v路径上的每一个顶点,使用edgeTo数组保存从s到该顶点的路径上的最后一个顶点坐标;而单点最短路径就是以同样的方式借助BFS保存从s到指定顶点的路径,这样得出的路径就是到达该顶点的最短路径。
三、环和无环图(拓扑排序)
在调度问题中,限制条件是这些任务的执行方法和起始时间,但最重要的限制条件叫做有限制级限制,它指明了任务间执行的先后顺序。
我们需要在一个有优先级限制的任务中,按该限制条件找出安排完成任务的顺序。这也等价于一个基本问题:拓扑排序,即在一个有向图中,将所有顶点排序,满足所有的有向边均从排在前面的元素指向排在后面的元素(或指出无法做到这一点)。
以高校课程安排为例,一些课程的开课必须要求学生修完前面的某些课,而拓扑排序就是在这种限制条件下,找出学生选修课程的顺序。
而一旦一个优先级限制的问题中存在有向环,那么这个问题一定是无解的。因此我们需要进行有向环的检测。
有向无环图就是不含有有向环的有向图
检测有向环的思路如下:
对有向图的每个顶点都进行DFS遍历,假设从顶点v开始深度优先遍历,将从该顶点递归调用路径上的所有顶点marked标记后再使用一个boolean[] onStack标记是否在递归栈上,如果对一个顶点的DFS递归调用没有发现有向环,则递归结束前再让该节点的onStack状态改为false;而如果对某个顶点的递归调用时发现另一个顶点已经被标记了,且onStack为true,则说明这个路径上一定存在有向环,这时将该环上的所有点加入Stack cycle栈中。
public class DirectedCycle {
private boolean[]marked;
private int[] edgeTo;
/**
* 有向环中的所有顶点(如果存在)
*/
private Stack<Integer>cycle;
/**
* 递归调用的栈上的所有顶点
*/
private boolean[] onStack;
public DirectedCycle(Digraph digraph) {
marked=new boolean[digraph.V()];
edgeTo=new int[digraph.V()];
onStack=new boolean[digraph.V()];
for (int v = 0; v < digraph.V(); v++) {
if (!marked[v]){
dfs(digraph,v);
}
}
}
/**
* 使用不带权的Digraph
* @param digraph
* @param v
*/
private void dfs(Digraph digraph, int v) {
onStack[v]=true;
marked[v]=true;
for (int w: digraph.adj(v)){
if (this.hasCycle()){
//如果已经找到有向环,则返回
return;
} else if (!marked[w]){
edgeTo[w]=v;
dfs(digraph,w);
}else if (onStack[w]){
cycle=new Stack<>();
for (int x = v; x != w; x=edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
}
}
//对v的一次递归调用后,如果没发现环,则重置为false
onStack[v]=false;
}
public Iterable<Integer>cycle(){
return cycle;
}
public boolean hasCycle(){
return cycle!=null;
}
}
测试:
public static void main(String[] args) {
Digraph digraph=new Digraph(4);
digraph.addEdge(0,1);
digraph.addEdge(2,3);
digraph.addEdge(3,1);
digraph.addEdge(1,2);
//存在环3>1->2>3
DirectedCycle cycle = new DirectedCycle(digraph);
if (cycle.hasCycle()){
System.out.println("存在环");
Stack<Integer> stack = cycle.cycle;
while (!stack.isEmpty()){
System.out.println(stack.pop());
}
}
}
结果:
存在环
3
1
2
3
《算法4》中给出:
一幅有向无环图的拓扑排序就是所有顶点的逆后排序
那么什么是逆后排序呢?
我们规定:
前序: 在对顶点v递归调用前就将该顶点加入队列,最后出队的顺序就是前序
后序:在对顶点v递归调用后将该顶点加入队列,最后出队的顺序就是后序
逆后序:在对顶点v递归调用后将该顶点加入栈中,最后出栈的顺序就是逆后序
实现如下:
/**
* 有向图中基于深度优先搜索的顶点排序
* @author MaoLin Wang
* @date 2020/2/2214:55
*/
public class DepthFirstOrder {
private boolean[]marked;
/**
* 所有顶点的前序遍历(递归调用前加入队列)
*/
private Queue<Integer> pre;
/**
* 所有顶点的后序遍历(递归调用后加入队列)
*/
private Queue<Integer> post;
/**
* 所有顶点的逆后序遍历(递归调用后压入栈)
*/
private Stack<Integer> reversePost;
public DepthFirstOrder(Digraph digraph) {
pre=new Queue<>();
post=new Queue<>();
reversePost=new Stack<>();
marked=new boolean[digraph.V()];
for (int v = 0; v < digraph.V(); v++) {
if (!marked[v]){
dfs(digraph,v);
}
}
}
private void dfs(Digraph digraph, int v) {
System.out.println("dfs("+v+")");
pre.enqueue(v);
marked[v]=true;
for (int w: digraph.adj(v)){
if (!marked[w]){
dfs(digraph,w);
}
}
System.out.println(v+"完成");
post.enqueue(v);
reversePost.push(v);
}
public Iterable<Integer>pre(){
return pre;
}
public Queue<Integer>post(){
return post;
}
public Iterable<Integer>reversePost(){
return reversePost;
}
}
我们先测试一下一张有向无环图的各个排序的顺序:
public static void main(String[] args) {
Digraph digraph = new Digraph(13);
digraph.addEdge(0,5);
digraph.addEdge(0,1);
digraph.addEdge(0,6);
digraph.addEdge(2,0);
digraph.addEdge(2,3);
digraph.addEdge(3,5);
digraph.addEdge(5,4);
digraph.addEdge(6,4);
digraph.addEdge(6,9);
digraph.addEdge(7,6);
digraph.addEdge(8,7);
digraph.addEdge(9,10);
digraph.addEdge(9,11);
digraph.addEdge(9,12);
digraph.addEdge(11,12);
DepthFirstOrder depthFirstOrder = new DepthFirstOrder(digraph);
Stack<Integer> reversePost = depthFirstOrder.reversePost;
}
调用结果及形成的队列如下:
边的构造顺序不一样,得到的拓扑排序也会不一样,但是结果一定是满足拓扑排序优先级限制的。
pre post reversePost
dfs(0) 0
dfs(6) 0 6
dfs(9) 0 6 9
dfs(12) 0 6 9 12
12完成 12 12
dfs(11) 0 6 9 12 11
11完成 12 11 11 12
dfs(10)0 6 9 12 11 10
10完成 12 11 10 10 11 12
9完成 12 11 10 9 9 10 11 12
dfs(4) 0 6 9 12 11 10 4
4完成 12 11 10 9 4 4 9 10 11 12
6完成 12 11 10 9 4 6 6 4 9 10 11 12
dfs(1) 0 6 9 12 11 10 4 1
1完成 12 11 10 9 4 6 1 1 6 4 9 10 11 12
dfs(5) 0 6 9 12 11 10 4 1 5
5完成 12,11,10,9,4,6,1,5 5 1 6 4 9 10 11 12
0完成 12,11,10,9,4,6,1,5,0 0,5,1,6,4,9,10,11,12
dfs(2) 0,6,9,12,11,10,4,1,5,2
dfs(3) 0,6,9,12,11,10,4,1,5,2,3
3完成 12,11,10,9,4,6,1,5,0,3 3,0,5,1,6,4,9,10,11,12
2完成 12,11,10,9,4,6,1,5,0,3,2 2,3,0,5,1,6,4,9,10,11,12
dfs(7) 0,6,9,12,11,10,4,1,5,2,3,7
7完成 12,11,10,9,4,6,1,5,0,3,2,7 7,2,3,0,5,1,6,4,9,10,11,12
dfs(8)
8完成 12,11,10,9,4,6,1,5,0,3,2,7,8 8,7,2,3,0,5,1,6,4,9,10,11,12
我们发现其逆后序就是我们要的拓扑排序,那么为什么逆后序就是拓扑排序呢?
对于任意边v->w,调用dfs(v)时,一定会出现以下三种情况之一:
1.dfs(w)已调用过,且已经结束(w被标记过了)
2.dfs(w)未被调用(w没被标记),因此dfs(v)时会调用dfs(w),且dfs(w)会在dfs(v)之前返回
3.dfs(w)被调用过了,且没有返回。这个就是有有向环时会出现的情况,但进行拓扑排序的前提的没有有向环,因为该情况不会出现。
因此 情况1和2都是w在v之前结束调用,则w在后序排序中,一定在v之前,相反,在逆后序中,w一定在v之后,因此对于任意v->w都是排名较前点指向排名较后的点。
这样我们就可以得到拓扑排序的实现:
public class TopologicalSort {
//顶点的拓扑排序
private Iterable<Integer>order;
public TopologicalSort(Digraph digraph) {
DirectedCycle directedCycle=new DirectedCycle(digraph);
//排序前进行有向环检测,没有环才可以进行拓扑排序
if (!directedCycle.hasCycle()){
//返回拓扑排序
DepthFirstOrder dfs=new DepthFirstOrder(digraph);
order=dfs.reversePost();
}
}
public Iterable<Integer>order(){
return order;
}
public boolean hasOrder(){
return order!=null;
}
}
四、有向图的强连通性
定义:
如果两个顶点是互相可达的,则称是强连通的。如果一个有向图的任意两个顶点都是强连通的,则该有向图是强连通的。
有向图的极大强连通子图,称为强连通分量(strongly connected components)。
如下:每个颜色代表一个强联通分量。
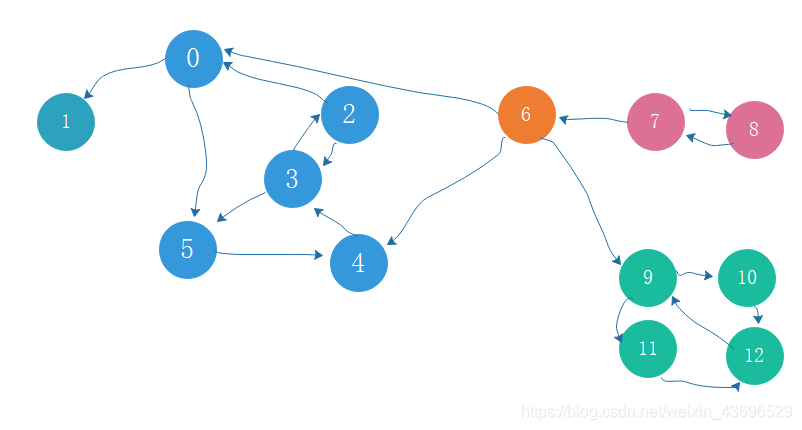
计算强连通分量的最常用的方法是Kosaraju算法:
其思想是:
1.使用DFS查找给定有向图G的反向图G^R
2.根据反向图G^R求得其逆后序列
3.对2求得的逆后序进行DFS遍历,访问未被标记的点
4.在构造函数中,所有在同一个dfs调用中被访问的顶点都在同一个强连通分量中,按无向图中求连通分量的方法求强连通分量。
有关该思想的证明如下:
我们只要证明以下两个问题即可:
(树上的证明猛一看可能看的不太懂,下面用自己的理解讲的细一点)
1.每个和s强连通的顶点v都会在构造函数调用的dfs(G,s)中被访问到
2.构造函数调用的dfs(G,s)所到达的任意顶点v都必然是和s强连通的。
对命题1,我们使用反证法:
1.假设一个和s强连通的顶点v在dfs(G,s)的调用中没有被访问到
2.由于存在一条从s->v的路径,所以如果顶点v没有在dfs(G,s)中被访问,就一定在之前调用了dfs(G,v),并且访问到了v。
3.又因为s和v是强连通的,所以也存在v->s的路径,在dfs(G,v)中,s一定会被标记,而s被标记,就一定不会再次进行dfs(G,s)的调用,矛盾,因此命题1成立。
对命题2:
1.要证明s和任意顶点v强连通,只要证明s->v且v->s,因为v是dfs(G,s)调用中访问到的任意顶点,所以一定存在s->v,接下来只要证明存在v->s即可。
2.要证明存在v->s,就相当于证明反向图中存在s1->v1
如下:
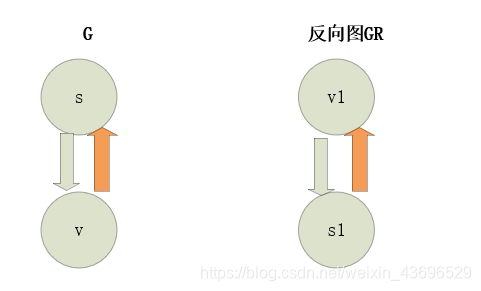
因为我们是按照逆后序进行深度优先遍历的,按照逆序,我们是在dfs(G,s)的调用中调用dfs(G,v),即先访问s再访问v,所以在反向图GR中,我们就应该是先访问v再访问s,对应上图GR中的点就是,先访问s1再访问v1。
即只要证明dfs(G,v1)在dfs(G,s1)之前结束,则这样就有如下两个情况:
1. dfs(G,v1)在调用dfs(G,s1)之前,且在dfs(G,s1)的调用开始前结束。
2. dfs(G,v1)在调用dfs(G,s1)之后,且在dfs(G,s1)的调用结束前结束。
如果出现情况1,这显然不可能,因为如果v1在s1之前就结束了,那么得出的逆后序应该是s1,v1,对应G中的v和s,先调用v再调用s,但是显然G是先调用s再调用v,所以该情况不存在。
如果是情况2,则说明存在一条路径s1>v1,即原图G中存在一条路径v->s,命题2正确。
下面是Kosaraju算法的实现:
/**
* 计算强连通分量的Kosaraju算法
* @author MaoLin Wang
* @date 2020/2/2216:54
*/
public class KosarajuSCC {
private boolean[] marked;
/**
* 强连通分量的标识符
*/
private int[] id;
/**
* 强连通分量个数
*/
private int count;
public KosarajuSCC(Digraph digraph){
marked=new boolean[digraph.V()];
id=new int[digraph.V()];
//求反向图的逆后序
DepthFirstOrder order=new DepthFirstOrder(digraph.reverse());
//对逆后序进行dfs遍历
for(int s: order.reversePost()){
if (!marked[s]){
dfs(digraph,s);
count++;
}
}
}
private void dfs(Digraph digraph, int v) {
marked[v]=true;
//顶点v属于第count个强连通分量
id[v]=count;
for (int w: digraph.adj(v)){
if (!marked[w]){
dfs(digraph,w);
}
}
}
/*v和w是否强连通*/
public boolean stronglyConnected(int v,int w){
return id[v]==id[w];
}
public int id(int v){
return id[v];
}
public int count(){
return count;
}
}
