在一个图G中,对于任意两个顶点u和v,若u可以到达v,v也可以到达u,那么图G称为连通图。如果该图为有向图,则称为强连通图。
设顶点的集合V1为V的一个子集,若由V1构成的子图为连通图,则称V1为连通子图;如果在连通子图V1中加入其他任何一个顶点都不构成连通图,则称V1为极大连通子图。无向图的极大连通子图称为连通分量;有向图的极大连通子图称为强连通分量。
有向图的强连通分量
有向图的强连通分量即为有向图的极大连通子图。下面介绍两种基于DFS求有向图的极大连通分量的方法。
Kosaraju算法




#include<iostream>
#include<vector>
#include<queue>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
int leave[vNum], belong[vNum], cnt = 0, bcnt = 0;
bool vis[vNum];
//对原图g进行dfs,得到顶点的处理完毕的序列
void dfs(vector<int>g[vNum], int cur) {
vis[cur] = true;
for (int i = 0; i < g[cur].size(); i++)
if (!vis[g[cur][i]])
dfs(g, g[cur][i]);
leave[++cnt] = cur; //顶点cur已处理完毕,加入leave
}
//对反图进行dfs,将所能访问的顶点设置为同一个强连通分量,当前强连通分量的编号为cnt
void dfst(vector<int>gt[vNum], int cur) {
vis[cur] = true;
belong[cur] = cnt; //将当前顶点的强连通分量编号设置为cnt
for (int i = 0; i < gt[cur].size(); i++)
if (!vis[gt[cur][i]])
dfst(gt, gt[cur][i]);
}
//Kosaraju算法求图g的强连通分量,gt为g的反图,v为顶点的数量,返回值为g的强连通分量的数量
int Kosaraju(vector<int>g[vNum], vector<int>gt[vNum], int v) {
int i;
memset(vis, 0, sizeof(vis));
for (i = 1; i <= v; i++) //对原图进行dfs
if (!vis[i])
dfs(g, i);
memset(vis, 0, sizeof(vis));
cnt = 0;
for (i = v; i >= 0; i--) //对反图进行dfs,从leave的最后一个元素所表示的顶点开始
if (!vis[leave[i]])
cnt++, dfst(gt, leave[i]);
for (i = 1; i <= v; i++) //输出每一个顶点及其所属的强连通分量
cout << i << " " << belong[i] << endl;
return cnt;
}
int main() {
}Tarjan算法
Kosaraju算法需要构建反图,并进行两次dfs。Tarjan算法求强连通图则只需要进行一次dfs,且不需要构建反图,在时间和空间效率上优于Kosaraju算法。
图的每个强连通分量为DFS树中的一颗子树,因此只要找到强连通分量在dfs树中子树的根结点。由于当出现反向边(u,v)时,在dfs树中v为u的祖先节点,因此dfs树中u和v之间的顶点就构成一个连通子图,Tarjan算法就是使得该连通子图极大化。
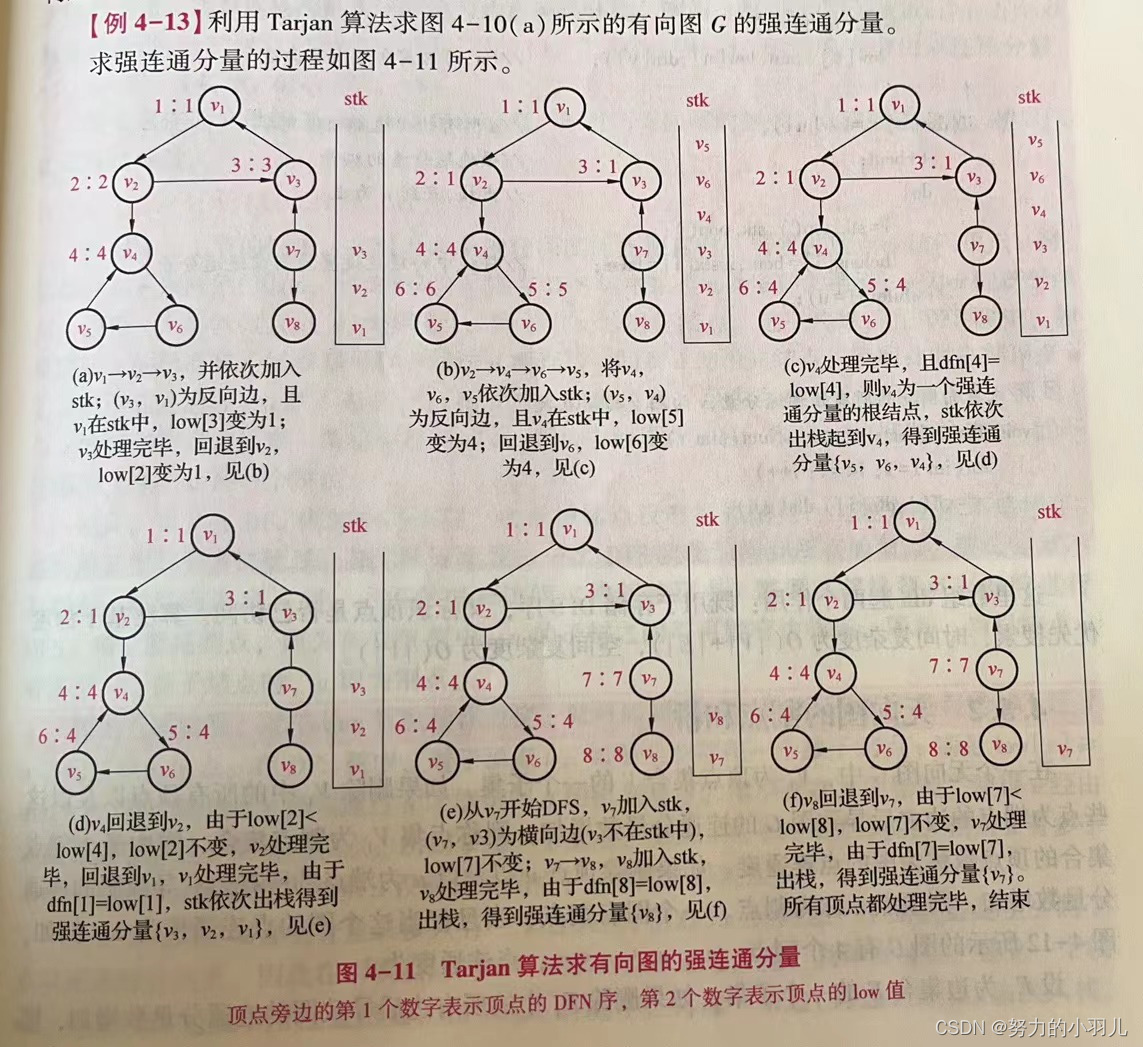
利用Tarjan求有向图的强连通分量
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
constexpr auto eNum = 102; //图的顶点数量
constexpr auto vNum = 200; //图的边的数量
typedef string dataType; //图顶点中存放数据信息的类型
typedef int datatype;
constexpr auto INF = 0x3f3f3f3f;
/*
dfn作用:1.存储dfs序 2.标记顶点是否已访问
(1)dfn:dfs序,即在dfs过程中访问每个顶点第一次访问的先后顺序(时间戳);
(2)low:low[u]表示u所在的当前连通子图所对应的dfs树中子树根结点的dfs序
(3)stk:栈,记录顶点已访问过但没有确定属于某个强连通分量的顶点
(4)instk:instk[u]=true时表示u在栈stk中,否则表示u不在栈中;
有两种情况下=false:u还没有访问到;u进栈后已出栈,此时已确定u属于某个强连通分量。
*/
int dfn[vNum]={0}, low[vNum], belong[vNum], cnt = 0, bcnt = 0;
bool instk[vNum];
stack<int>stk;
//对图g进行深度优先搜索,从u出发
void dfs(vector<int>g[vNum], int u) {
int i, v;
dfn[u] = low[u] = ++cnt; //初始时dfn和low的值相同
stk.push(u), instk[u] = true;
for (i = 0; i < g[u].size(); i++) {
v = g[u][i];
if (!dfn[v]) {
dfs(g, v);
low[u] = min(low[u], low[v]);//(u,v)为树边
}
else if (instk[v])
low[u] = min(low[u], dfn[v]); //(u,v)为前向边或反向边
}
if (dfn[u] == low[u]) { //u所有的出边都处理完毕
++cnt; //强连通分量的编号
do { //出栈,直达u为止
i = stk.top(), stk.pop();
belong[i] = bcnt, instk[i] = false; //将栈中的顶点设置为当前连通分量
} while (i != u);
}
}
//求有向图g的所有强连通分量,v为图g的顶点数
void Tarjan(vector<int>g[vNum], int v) {
for (int i = 1; i <= v; i++)
if (!dfn[i])
dfs(g, i);
}
int main() {
}