【关于四足机器人那些事】雅克比矩阵

一、引入

假设有6个函数，每个函数有6个独立的变量，即：

$\begin{matrix} y_1 = f_1(x_1, x_2, x_3, x_4, x_5, x_6)\\ y_2 = f_2(x_1, x_2, x_3, x_4, x_5, x_6)\\ \vdots \\ y_6 = f_6(x_1, x_2, x_3, x_4, x_5, x_6)\\ \end{matrix}$

我们用矢量形式表达上式，即：

$Y = F(X)$

现在，如果我们要计算 $y_i$的微分关于 $x_i$的微分的函数，通过多元函数求导法则，可以计算出：

$\begin{matrix} \delta y_1 = \frac{\partial f_1}{\partial x_1}\delta x_1 + \frac{\partial f_1}{\partial x_2}\delta x_2 + \cdots + \frac{\partial f_1}{\partial x_6}\delta x_6 \\ \\ \delta y_2 = \frac{\partial f_2}{\partial x_1}\delta x_1 + \frac{\partial f_2}{\partial x_2}\delta x_2 + \cdots + \frac{\partial f_2}{\partial x_6}\delta x_6\\ \vdots \\ \delta y_6 = \frac{\partial f_6}{\partial x_1}\delta x_1 + \frac{\partial f_6}{\partial x_2}\delta x_2 + \cdots + \frac{\partial f_6}{\partial x_6}\delta x_6 \end{matrix}$

同样，我们以矢量形式表示：

$\delta Y = \frac{\partial{F}}{\partial{X}}\delta X \tag{1}$

式（1）中的 $\frac{\partial{F}}{\partial{X}}$为 $6\times6$偏导数矩阵。它，就是我们所说的雅克比矩阵 $J$

速度映射

如果 $f_1(X)$到 $f_6(X)$都是非线性函数，那么，这些偏导数都是关于 $x_i$的函数，我们可以用以下式子表达：

$\delta Y = J(X) \delta X \tag{2}$

式（2）两边同时除以时间微分 $d_t$，我们就可以将雅克比矩阵看作是 $X$中的速度映射为 $Y$中的速度：

$\dot{Y} = J(X)\dot X$

在任一瞬间，X都有一个确定的值， $J(X)$是个线性变换，在每一新时刻，如果X发生改变， $J(X)$也会发生改变

在机器人学中，通常使用雅克比将关节速度与操作臂末端的速度联系起来：

$v = J(\theta)\dot \Theta \tag 3$

其中， $\Theta$为关节角组成的向量， $v$为速度向量。对于6关节机械臂，雅克比矩阵为 $J \in \mathbb{R}^{6\times6}$，关节角 $\Theta \in \mathbb{R}^{6\times1}$，速度 $v \in \mathbb{R}^{6\times1}$，而 $v$是由一个 $3\times1$的线速度和一个 $3\times1$的角速度所组成，表达为：

$v = \begin{bmatrix} v\\ \omega \end{bmatrix}$

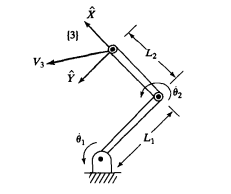
对于两连杆机构，如下图，我们很容易写出它的关节速度(世界坐标系下)与执行器末端速度的关系：

$v_w = \begin{bmatrix} -l_1s_1\dot\theta_1-l_2s_{12}(\dot \theta_1 + \dot \theta_2)\\ l_1c_1\dot \theta_1 +l_2c_{12}(\dot \theta_1 \dot \theta_2)\\ 0 \end{bmatrix} = \begin{bmatrix} -l_1s_1-l_2s_{12} & -l_2s_{12}\\ l_1c_1 + l_2c_{12} & l_2c_{12} \\ 0 &0&0 \end{bmatrix} \begin{bmatrix} \dot \theta_1\\ \dot \theta_2 \\ 0 \end{bmatrix}$

以及相对于执行器末端的速度：

$v_b = \begin{bmatrix} l_1s_2 \dot \theta_1 \\ l_1c_2\dot \theta_1 + l_2(\dot \theta_1 +\dot \theta_2) \\ 0 \end{bmatrix} = \begin{bmatrix} l_1s_2 & 0 &0\\ l_1c_2+l_2 & l_2 &0 \\ 0& 0&0 \end{bmatrix} \begin{bmatrix} \dot \theta_1\\ \dot \theta_2 \\ 0 \end{bmatrix}$

因此，我们能够算出世界坐标系的雅克比矩阵为：

$J_w(\Theta) = \begin{bmatrix} -l_1s_1-l_2s_{12} & -l_2s_{12}\\ l_1c_1 + l_2c_{12} & l_2c_{12} \end{bmatrix}$

末端执行器坐标系下的雅克比：

$J_b(\Theta) = \begin{bmatrix} l_1s_2 & 0\\ l_1c_2+l_2 & l_2 \end{bmatrix}$