到底谁是异常 (多元高斯分布异常点检测)

异常点检测 (Outlier Detection) 相信大家并不陌生，它是无监督学习的重要应用之一，它的主要任务是从一些列无标签的样本中找到某些 “与众不同的” 的样本 (异常点 Outlier)，这些样本与大部分样本 (正常点 Normal) 的分布“格格不入”。这篇文章主要介绍基于独立高斯分布 (Gaussian distribution) 和多元高斯分布 (Multi-variable Gaussian distribution) 的异常点检测法。

1. 高斯分布

高斯分布 (Gaussian distribution)¹ 也就是我们常讲的 正态分布 (Normal distribution)，被人称为“上帝分布”。它在很大程度上揭露了自然界中的事物分布的基本规律，即呈“中间多，两头少” 的趋势，如全国人民的身高、全国人民的工资等都可以视作服从高斯分布。

假定包含 $m$ 个样本的随机变量 $X=\{x^{(1)},x^{(2)},...,x^{(m)}\}$ 满足高斯分布，记为 $X \sim N(\mu,\sigma^2)$，其中 $\mu$ 表示 $X$ 的数学期望， $\sigma^2$ 表示 $X$ 的样本方差。我们有，

$\mu = \frac{1}{m}\sum_{i=1}^{m} x^{(i)}, \ \sigma^2 = \frac{1}{m} \sum_{i=1}^{m}(x^{(i)}-\mu)$

更进一步，我们用 概率密度函数 $f(x)$ 来表示随机变量 $X$， $f(x)$ 表示了 $X$ 取 $x$ 时的概率。整个 $p(x)$ 的曲线呈 “钟型”，因此 $f(x)$ 也称为 “钟型曲线”。

$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp(-\frac{|x-\mu|^2}{2\sigma^2})$

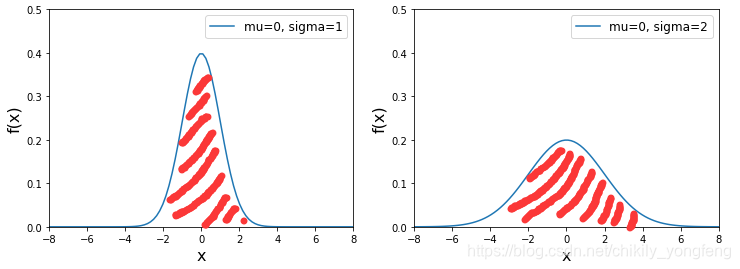
下图给出了不同 $\mu,\sigma^2$ 值的组合的 $f(x)$ 的趋势图 (注意图中红色阴影面积为 1)，其中期望 $\mu$ 决定了曲线的位置，方差 $\sigma^2$ 决定了曲线的平缓程度。

2. 独立高斯分布的异常点检测方法

独立高斯分布假定每个维度都服从高斯分布，且彼此之间相互独立 (没有相关性)。为了更好的展示独立高斯分布的方法，我们考虑如下 A,B,C 三种情形。

情形 A：假设 $X$ 是一维随机变量，维度为 $x_1$，该维度服从高斯分布 (满足 $x_1 \sim N(\mu_1,\sigma_1^2)$)，即 $X$ 变量可看做是是数轴 $x_1$ 上的点。我们设定阈值 $\epsilon$，认为当 $p(x)<\epsilon$ 时，样本 $x$ 是异常点；当 $p(x)>\epsilon$ 时，样本 $x$ 是正常点。于是我们在一维数轴上建立新的维度 $p(x)$，用 $p(x)=\epsilon$ 来划分，在线下的点即为异常点。

综上，针对样本 $x=a_1$，我们判断其是否是异常点的方法为：计算 $p(x)$ 是否小于 $\epsilon$，若小于则标记为异常点。

$p(x) = f(a_1) = \frac{1}{\sqrt{2\pi \sigma_1^2}} \exp(-\frac{(a_1-\mu_1)^2}{2\sigma_1^2})$

情形 B：假设 $X$ 是二维随机变量，维度为 $x_1,x_2$，且每个维度都服从高斯分布 (满足( $x_1 \sim N(\mu_1,\sigma_1^2)$，和 $x_2 \sim N(\mu_2,\sigma_2^2)$))，即 $X$ 变量可看做是平面直角坐标系 ( $x_1,x_2$) 上的点。我们依然设定阈值 $\epsilon$ 来判断样本是否是异常点。我们在二维平面上建立新的维度 $p(x)$，如下图所示,

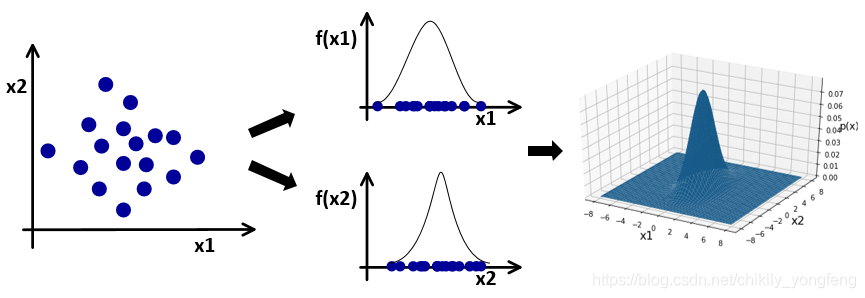
综上，针对二维随机变量 $x=(a_1,a_2)^T$，我们判断异常点的方法为：计算 $p(x)$ 是否小于 $\epsilon$，若小于则标记为异常点。 其中 $\mu_1,\sigma_1^2$ 表示 $x_1$ 维度上的期望和方差， $\mu_2,\sigma_2^2$ 表示 $x_2$ 维度上的期望和方差。

$p(x) = f(a_1)\times f(a_2) = \frac{1}{\sqrt{2\pi \sigma_1^2}} \exp(-\frac{(a_1-\mu_1)^2}{2\sigma_1^2})\times \frac{1}{\sqrt{2\pi \sigma_2^2}} \exp(-\frac{(a_2-\mu_2)^2}{2\sigma_2^2})$

情形 C：假定 $X$ 是 $n$ 维随机变量，维度为 $x_1,x_2,...,x_n$，且每个维度都服从高斯分布 (满足 $x_i \sim N(\mu_i,\sigma_i^2), \ i=1...n$)，此时 $X$ 变量不能够以可视化的方式呈现出来。

根据之前情形 A 和情形 B 的推断，判断 $n$ 维度样本 $x=(a_1,a_2,...,a_n)^T$ 是否是异常点的方法为：计算 $p(x)$ 是否小于 $\epsilon$，若小于则标记为异常点。其中 $\mu_i,\sigma_i^2$ 表示 $x_i$ 维度上的期望和方差。

$p(x) = \prod_{i=1}^{n}f(a_i) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi \sigma_i^2}} \exp(-\frac{(a_i-\mu_i)^2}{2\sigma_i^2})$

根据上述 A,B,C 三种情形我们可知，对于多维随机变量，我们 将所有维度上的概率密度函数相乘，然后在判断其值是否小于阈值 $\epsilon$。若大于或等于于阈值则该点是正常点；若小于阈值则该点是异常点。这种方法需要假设随机变量的每个维度都服从高斯分布不考虑各个维度之间的关系，我们称这种方法为 独立高斯分布 的异常点检测方法。

3. 多元高斯分布的异常点检测

考虑二维随机变量 $X$，它的两个维度分别是 $x_1,x_2$ 且相互之间有正相关关系。如果我们沿用第一节中的独立高斯分布的方法来检测异常点，那么正常点区域是一个“正的”椭圆。但是事实上，由于 $x_1,x_2$ 具有正相关性，因此正确的正常点区域应该是一个“斜的”椭圆。造成这个结果的原因是 独立的高斯分布检测方法没有考虑到维度之间的相关性！

为了解决上述问题，科学家们使用了一种叫 多元高斯分布²³ (也称 联合高斯分布) 的异常点检测方法。该方法能够自动的找出维度之间的相关性，即自动的生成“斜的”椭圆区域。

任务：针对包含 $m$ 个样本的数据集 $T=\{x^{(1)},x^{(2)},...,x^{(m)}\}$，每个样本都是 $n$ 维的向量 $x^{(i)}\in \R^{n\times1}$，判断样本 $x=(a_1,a_2,...,a_n)^T$ 是否是异常点。

方法：计算 $p(x)$ 的值并与预定的阈值 $\epsilon$ 比较。若 $p(x)<\epsilon$ 则样本 $x$ 是异常点，否则 $x$ 是正常点。 $p(x)$ 的计算方式如下，

$p(x) = \frac{1}{(2\pi)^{(n/2)}|\Sigma|^{(1/2)}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$

其中 $\mu$ ( $n$ 维度列向量) 展示了所有维度的期望， $\Sigma$ 表示协方差矩阵 ( $n\times n$ 维)。二者的计算公式如下，

$\mu = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}, \ \ \Sigma = \frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T$

效果：现在讨论一下多元高斯分布是如何找出 $x_1,x_2$ 的相关性的，下图给出了 6 种 $\mu,\Sigma$ 的组合，每种组合都对应着不同的检测区域 (即椭圆的形状)。我们可以看到，多元高斯分布主要通过控制 $\Sigma$ 的值来控制椭圆的形状，形状的不同则反映了相关度的不同。

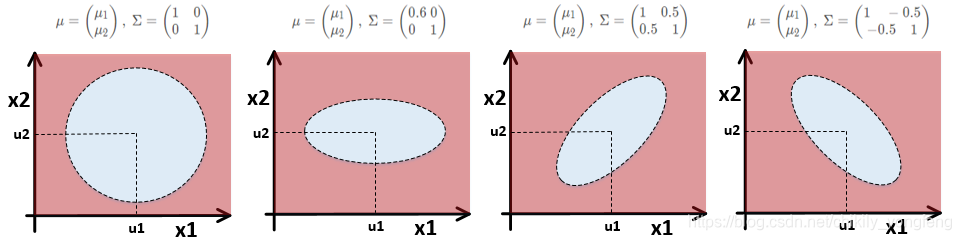
上图的前 2 个子图反映了独立高斯分布的检测区域，即“正”的椭圆， $x_1,x_2$ 之间没有相关性。后 2 个子图反映了多元高斯分布的检测区域，即“斜”的椭圆，分别表示正相关和负相关。

在独立高斯分布和多元高斯分布中，阈值 $\epsilon$ 的设定直接关系到异常点的数量。若 $\epsilon$ 过高，则会有很大一部分样本被识别为异常点；若 $\epsilon$ 过低，则很有可能全部样本都被识别为正常点。因此，在实际应用中，人们往往按一定的比例或经验来设置 $\epsilon$ 的值。

4. 独立高斯分布与多元高斯分布的比较

(1) 独立高斯分布假设维度之间是相互独立的，通过计算每个维度的概率分布的累积和来判断样本是否是异常的。它的优点是 直观且计算量较少，缺点是 不能考虑维度之间的相关性。

(2) 多元高斯分布通过计算整体维度的分布特性，通过 $\Sigma$ 能够自动的搜索各个维度间的相关关系，但它的缺点也很明显就是 计算量大 (主要关于 $\Sigma$ 的计算)，并且一旦维度 $n$ 过小，或者维度之间出现冗余， $\Sigma$ 极有可能无法求逆，这也带给多元高斯分布的检测带来困难。

因此，根据实际情况来选择运用那种分布十分重要，当特征维度过大时 (如 $n>100,000$)，或过小时 (如 $n\gg m$)，我们优先考虑独立高斯分布。当特征维度正常且之间包含很强的相关性时，我们优先考虑多元高斯分布。

---

1. hhaowang. 正态分布 (高斯分布) (博客). Link ↩︎

2. bingjianing. 多元高斯分布 (The Multivariate normal distribution) (博客). Link ↩︎

3. Linghan Zhang. 多元高斯分布完全解析. Link ↩︎