
把无监督学习分成两种
一种是化繁为简,可以分成两大类:聚类和降维
所谓的化繁为简的意思是说,找一个函数,可以input看起来像树的东西,output都是抽象的树,把本来复杂的东西,变成比较简单的output。在做无监督学习时,通常只会有函数中的一边。比如找一个函数,可以把所有的树都变成抽象的树,但是拥有的数据,只有一大堆各种不同的图像,不知道它的output长什么样子。
另外一种是无中生有,找一个函数,随机给它一个input(比如一个数字1),然后output一棵树,输入数字2,output另外一棵树,输入3,又是另外一棵树。输入一个随机数,就自动画一张图出来,不同的数画出来的图不一样。这个任务里面,要找的可以画图的函数,只有output没有input。只有一大堆的图像,但是不知道输入什么数字才可以得到这些图像。
聚类
K-means聚类
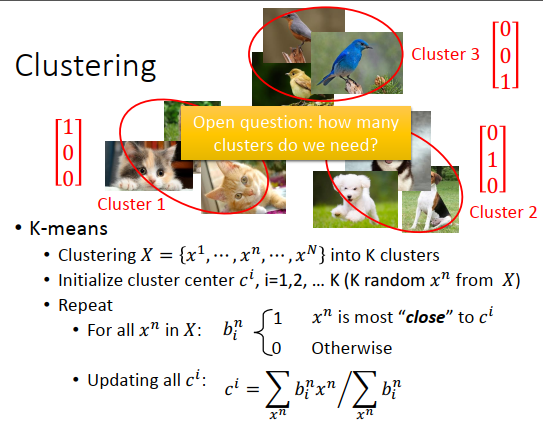
什么是聚类?
假设做图像的聚类,现在有一大堆的图像,然后把它们分成一类一类的。之后可以说,上图左边的图像都属于簇1,右边的图像都属于簇2,上方的图像都属于簇3,就像贴标签的意思,把本来有些不同的图像,都用同一个class表示,就做到化繁为简这件事情。
这里最关键的问题是到底要有几个簇,这个就跟神经网络是几层一样,是依赖经验的,当然也不能太多,比如多到说9张图像9个簇,那聚类就没有意义,直接每个图像一个簇就好了,或者说全部图像都是一个簇,也跟没有做一样。
聚类方法最常用的就是K-means,有一大堆未标注数据\(x^1\)到\(x^N\),每一个\(x\)代表一张图像,做成k个簇。
怎么做?
先找簇的中心,假如每一个对象都用一个向量表示,有\(K\)个簇就需要\(c^1\)到\(c^K\)个中心。
可以从训练数据里随机找\(K\)个对象出来作为初始化中心。
对所有数据,决定属于哪一个簇,假设\(x^n\)和\(c^i\)最接近,那么\(x^n\)就属于\(c^i\),用\(b_i^n\)表示。然后更新簇,所有属于\(c^i\)的数据做平均,就是第\(i\)个簇新的中心,更新要反复进行。
之所以从数据集挑选\(K\)个样本做初始化簇中心,有一个很重要的原因是,如果是纯粹随机的(不从数据集里挑),那很可能在第一次分配这个簇中心的时候,没有任何一个样本跟这个中心很像,也可以说这个簇没有任何样本,再次更新就会出错。
层次聚类
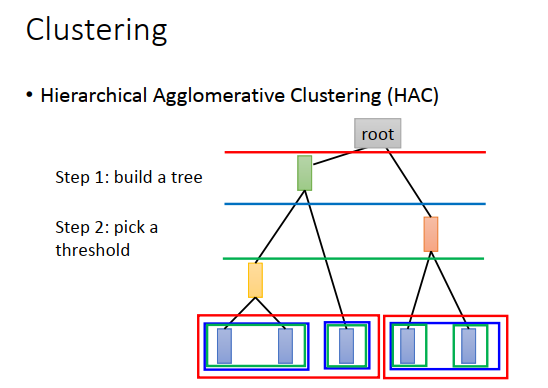
假设有5个样本做层次聚类,先要做一个树结构。计算两两样本的相似度,挑出最相似的数据对。
比如第一个和第二个样本最相似,那就合并(比如用平均值代表),5个样本变为4个样本;再计算相似度,配对的是4,5样本,然后把他们合并(平均值),变成3个样本;接着计算相似度,配对的是黄色数据点和剩下的蓝色数据点,再次合并(平均),最后只剩红色和绿色,那么最后平均起来得到root。根据5笔数和之间的相似度,就建立出了一个树结构。
树结构只是告诉我们说哪些样本比较像,还没有做聚类。
怎么做聚类?
接下来要决定在这棵树上切一刀,
比如在上图蓝线初切一刀,意味着把数据分成3簇,1、2为一簇,3单独为一簇,4、5为一簇。
在红色线切一刀,则1、2、3为一簇,4、5为一簇。
在绿色点切一刀,则1、2为一簇,3、 4、 5单独为一簇。
层次聚类和K-means的差别
如何决定你簇的数目,在K-means里要自己决定k的值,而在层次聚类里要决定的是在哪里切一刀,如果切比较容易考虑的话,那层次聚类可能更好。
Distributed Representation

光做聚类的话是很卡的,做聚类就是以偏概全,因为每个对象都必须属于某一个簇。就好像念力分成6大类,每个人都会被分配到6个大类其中一类,但是这样分配太过粗糙,比如某个人的能力既有强化系的特性又有放出系的特性,只分为一类就会丢失很多信息,应该像上图左下方一样进行表示。
只分为一类就是以偏概全了,应该要用一个向量来表示每个对象,向量的每个维度代表了某一种特质(属性)。这件事情叫做Distributed Representation。
如果对象是一个高维的东西,例如图像,现在用它的特性来表示,就会把它从高维空间变成低维空间,这件事情叫做降维。Distributed Representation和降维是一样的东西,不同的称呼。
降维
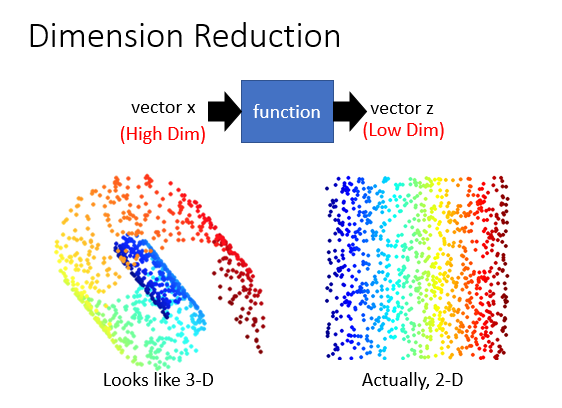
为什么降维有用?
假设数据分布如上图左边,在3D空间里分布是螺旋的样子,但是用3D描述数据分布比较浪费的,直觉上也可以感觉可以摊开变成右边2D的样子,只需要2D的空间就可以描述3D的信息。在3D空间里面解比较麻烦,那就在2D里做这个任务。
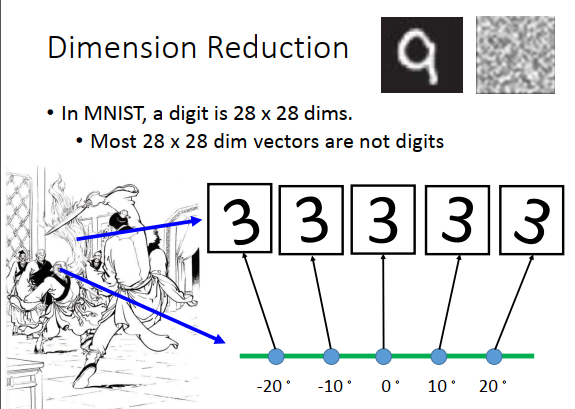
考虑一个比较具体的例子MNIST,在MNIST里面,每一个input的数字都是28*28的矩阵来描述。但是实际上,多数28 * 28矩阵转成一个图像看起来都不像数字,在28 * 28空间里是数字的矩阵是很少的。所以要描述一个数字,或许不需要用到28 * 28维,远比28 * 28维少。
所以举一个极端的例子,有一堆3,从像素点看要用28 * 28维来描述每张图像。实际上,只要用一个维度就可以表示,中间的是3,其他的3都是中间的3左转右转10、 20度。所以唯一需要记录的就是中间的3,左转和右转了多少度,即只需要角度的变化,就可以知道28维空间中的变化。

怎么做降维?
找一个函数,input是一个向量x,output是另外一个向量\(z\)(\(z\)的维度比\(x\)小)。
在降维里最简单的方法是特征选择,把数据的分布拿出来看一下, 在二维平面上发现数据集中在\(x_2\)维度,所以\(x_1\)这个维度没什么用,那么就把他拿掉,等于是降维这件事。特征选择不一定有用,有可能case里面任何一个维度都不能拿掉。
另一个常见的方法是PCA,函数是一个很简单的线性函数,input \(x\)和output \(z\)之间的关系就是一个线性的transform,即\(x\)乘上一个矩阵\(W\) 得到\(z\) 。现在不知道\(z\)长什么样子,要根据一大堆的\(x\)把\(W\)找出来。
PCA-投影角度
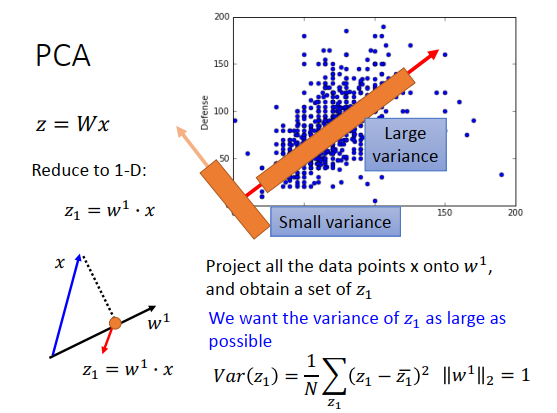
刚才讲过PCA要做的事是找\(W\),假设一个比较简单的case,考虑一个维度的case。假设要把我们的数据投射到一维空间上,即\(z\)只是一维的向量。\(w^1\)是\(W\)的第一行,和\(x\)(列向量)做内积都到一个标量\(z_1\)。
\(w^1\)应该长什么样子?
首先假设\(w^1\)的长度是1,即\(||w^1||_2=1\),一定要有这个假设。
如果\(||w^1||_2=1\),\(w^1\)是高维空间中的一个向量,那么\(z_1就是\)就是\(x\)在\(w^1\)上的投影长度。
现在做的事情就是,求出每一个\(x\)在\(w^1\)上的投影,那\(w^1\)应该长什么样子?
举个例子,假设上图右上方是\(x\)的分布,\(x\)都是二维的,每个点代表一只宝可梦,横坐标是攻击力,纵坐标是防御力。今天要把二维投影到一维,应该要选什么样的\(w^1\)?可以选$w^1 $如上图右上方右斜方向,也可以选左斜方向,选不同的方向,最后得到的投影的结果会不一样。
那总要给我们一个目标,我们才知道要选什么样的\(w^1\),现在目标是经过投影后得到的\(z_1\)的分布越大越好。我们不希望投影后所有的点都挤在一起,把本来数据点之间的奇异度消去。我们希望投影后,数据点之间的区别仍然看得出来,那么我们可以找投影后方差越大的那个\(w^1\) 。
看上面的例子,如果是右斜方向,那么方差较大,左斜方向方差则较小,所以更可能选择右斜方向作为\(w^1\)。
从上面的例子里看,\(w^1\)代表了宝可梦的强度,宝可梦可能有一个隐藏的向量代表它的强度,这个隐藏的向量同时影响了防御力和攻击力,所以防御力和攻击力会同时上升。
如果要用方程表示,就会说现在要去最大化的对象是\(z_1\)的方差。

假设知道怎么做,解一下\(W\)。找到一个\(w^1\),让\(z_1\)的方差最大。
接下来,你可能不想投影到一维的,想投影到二维平面,这时候就把\(x\)和另一个\(w^2\)做内积得到\(z_2\)。
\(z_1,z_2\)串起来就是\(z\),\(w^1,w^2\)的转置排起来就是\(W\)的第一行和第二行。
找\(z_2\)和找\(z_1\)一样,首先\(w^2\)的2-norm是1,希望\(z_2\)的分布越大越好,但是如果只是让\(z_2\)的方差越大越好,那找出来的就是\(w_1\)(因为\(w_1\)是让投影方差最大的),那么就需要再加一个约束。这个约束是,\(w_2\)要跟之前找出来的\(w_1\)正交(\(w_1\)和\(w_2\)的内积为0)。借助这个方法,你想投影到K维,就找\(w_1,w_2,...,w_k\)分别作为\(W\)的行。
找出来的\(W\)会是一个单位正交矩阵,\(w_i,w_j\)是正交的,\(w_1和w_2\)的2-norm都是1。

怎么解\(w_1,w_2\)?
其实要用拉格朗日乘子法。\(\bar{z_1}\)是\(z_1\)的均值,\(\bar{z_1}\)是summation over所有\(w^1\)跟\(x\)的内积,summation 跟\(w^1\)无关,把\(w^1\)提出来变为\(\large \bar{z_1}=w^1 \cdot \sum x=w^1\cdot \bar{x}\),得到\(w^1\)跟\(x\)的平均的内积。
我们要最大化的对象是\(z_1\)的方差(计算公式如上图),\(a^Tba^Tb=a^Tb(a^Tb)^T\)中可以变为\((a^Tb)^T\)的原因是\(a^Tb\)是一个标量,标量转置仍为自身。
summation over在\(x\)上,和\(w^1\)无关,看上图左下方蓝色框框,蓝色框框内是\(x\)的协方差矩阵公式。
\(x\)的形式应该为\(\begin{bmatrix} \bf{x_1\\x_2\\ \vdots \\ x_n} \end{bmatrix}\),转置则为\(\begin{bmatrix} \bf{x_1^T }& \bf{x_2^T} & \cdots & \bf{x_n^T} \end{bmatrix}\) ,注意里面每个\(\bf{x}\)都是一个向量,代表一个维度的所有样本数值,例如协方差矩阵第一个元素为(假设\(x_1\)已经是减去均值后的值)
\(\frac{1}{N} \begin{bmatrix} x_1^1 & x_1^2 & \cdots & x_1^N\end{bmatrix}\)\(\begin{bmatrix} x_1^1 \\ x_1^2 \\ \cdots \\ x_1^N\end{bmatrix}=\frac{1}{N}((x_1^1)^2+(x_1^2)^2+\cdots +(x_1^N)^2)\)就是变量\(x_1\)与\(x_1\)的协方差,同理
\(\frac{1}{N} \begin{bmatrix} x_1^1 & x_1^2 & \cdots & x_1^N\end{bmatrix}\)\(\begin{bmatrix} x_2^1 \\ x_2^2 \\ \cdots \\ x_2^N\end{bmatrix}=\frac{1}{N}(x_1^1 x_2^1+x_1^2x_2^2+\cdots +x_1^Nx_2^N)\)就是变量\(x_1\)与\(x_2\)的协方差。
我们用\(S\)来描述\(x\)的协方差矩阵,现在问题变为要找一个\(w^1\),最大化\((w^1)^TSw^1\),但是这个最大化对象是有约束条件的,如果没有约束条件的话,那把\(w^1\)每一个值都变得无穷大就结束了。
它的约束是\(w^1\)的2-norm要等于1。

\(S\)是\(x\)的协方差矩阵,对称且半正定的(所有的特征值都是非负的)。这里先给出结论,\(w^1\)是协方差矩阵对应最大特征值的特征向量。
中间的计算过程需要用拉格朗日乘子法,加上约束后的目标函数为\(g(w^1)\),然后\(g\)对所有\(w\)(\(w\)是一个向量)做偏微分等于0,整理后得到一个式子\(Sw^1=\alpha w^1\),那么\(w^1\)就是\(S\)的一个特征向量。
但是\(S\)有很多个2-norm为1的特征向量,接下来要做的事情就是找使\((w^1)^TSw^1\)最大的\(w^1\)。把\((w^1)^TSw^1\)整理成\(\alpha (w^1)^Tw^1\),由于\((w^1)^Tw^1=1\),最后变为\(\alpha\) 。
当\(w^1\)对应最大的特征值时,\(\alpha\)最大(即是最大的特征值\(\lambda _1\))。
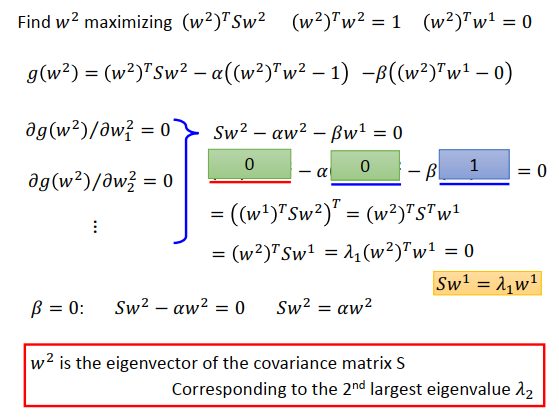
要找投影向量\(w_2\)(投影到\(w_2\)的方差第二大)的时候,要解的是上图最上方的式子。最大化在\(w_2\)上投影的方差\((w^2)^TSw^2\),同时要有约束\((w^2)^Tw^2=1\)和\((w^2)^Tw^1=0\),\(w^2\)和\(w^1\)要是正交的。解这个问题,会发现\(w^2\)也是协方差矩阵的一个特征向量,对应到第二大的特征值\(\lambda_2\)。
再次使用拉个朗日乘子法,如上图最上方第二行所示,要加上两个约束条件,拉格朗日乘子为\(\alpha\)和\(\beta\)。
接下来对\(w^2\)里每个参数做偏微分,做完之后得到式子\(Sw^2-\alpha w^2-\beta w^1=0\)
然后左边同乘\(w^1\)的转置变成\((w^1)^TSw^2-\alpha (w^1)^T w^2-\beta (w^1)^T w^1=0\),
由于\((w^1)^Tw^1 =1,(w^1)^Tw^2=0\),而\((w^1)^TSw^2\)是一个标量,转置等于自身,则
$(w1)TSw^2-\alpha (w1)T w^2-\beta (w1)T w^1=0 \ ((w1)TSw2)T -\alpha \times0-\beta\times1=0 $
因为\(S\)是对称的,转置等于自身,则\(((w^1)^TSw^2)^T=(w^2)^TS^Tw^1=(w^2)^TSw^1\),那么
\((w^1)^TSw^2-\alpha (w^1)^T w^2-\beta (w^1)^T w^1=0 \\ ((w^1)^TSw^2)^T -\alpha \times0-\beta\times1=0 \\ (w^2)^TSw^1-\beta=0\)
我们知道\(Sw^1=\lambda_1w^1\)(计算特征值的公式),那么
\((w^1)^TSw^2-\alpha (w^1)^T w^2-\beta (w^1)^T w^1=0 \\ ((w^1)^TSw^2)^T -\alpha \times0-\beta\times1=0 \\ (w^2)^TSw^1-\beta=0 \\ (w^2)^T\lambda_1w^1=\beta=0\)
我们得到的结论是\(\beta=0\),那么原式变为\(Sw^2-\alpha w^2=0\),即\(Sw^2=\alpha w^2\)。所以知道\(w^2\)又是一个特征向量。
$(w2)TSw2=(w2)^T\alpha w^2=\alpha \(,那么\)(w2)TSw2$就等于特征值,是第二大的特征值,因为$w1\(已经对应了最大的特征值。因为\)S$是对称的,那么不同特征值对应的特征向量是正交的。

\(z\)的协方差矩阵是对角矩阵,也就是说如果做PCA,原来的数据分布可能是上图右上方左边的图,做完PCA后,会做去相关性,让不同的维度间的协方差为0,也就是说\(z\)是对角矩阵。
去相关性让\(z\)为对角矩阵有什么用?
假设\(z\)是PCA后得到的新特征,使用新特征训练model,假设model是一个生成模型,用高斯来描述某一个类别的分布,而使用高斯,就已经假设了输入数据的协方差矩阵是对角矩阵(假设不同维度之间没有相关性),这样可以减少参数量。使用维度不相关的数据来训练生成模型,那么就可以用简单的模型,防止过拟合的问题。
为什么\(z\)的协方差矩阵是对角矩阵?
\(z\)的协方差计算公式如上图所示,\(S\)是\(x\)的协方差矩阵,\(W^T\)的第一列为\(w^1\)。
\(w^1\)是\(S\)的特征向量,所以\(Sw^1=\lambda_1 w^1,Sw^k=\lambda_k w^k\),\(\lambda\)是特征值。
\(w^1\)是\(W\)的第一行,而\(W\)是一个正交矩阵,所以\(W \cdot w^1=\begin{bmatrix} w^1 \\ w^2 \\ \vdots \\ w^k\end{bmatrix}\begin{bmatrix} w^1 \end{bmatrix}=\begin{bmatrix} 1 \\0 \\ \vdots \\0 \end{bmatrix}\),是第一个维度为1,其余维度为0的向量\(e_1\)。\(W \cdot w^k=e_k\),\(e_k\)的第k维是1,其余都是0。
PCA-另外一个角度
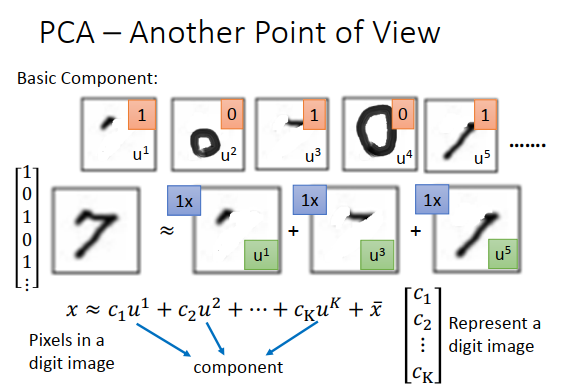
假设现在考虑手写数字识别,我们知道只写数字其实是由一些基本成分组成的,这些基本成分可能是笔画。例如斜的直线,横的直线,比较长的直线,小圈、大圈等等,这些基本成分加起来以后得到一个数字。
基本成分我们写作\(u^1,u^2,u^3...\),这些基本的成分其实就是一个一个的向量。考虑MNIST数据集,一张图像是28 * 28像素,就是28*28维的向量。基本成分其实也是28 * 28维的向量,把这些基本成分向量加起来,得到的向量就代表了一个数字。
如果写成公式的话,就如上图最下方所示的公式。\(x\)代表某一张图像的像素,用向量表示。\(x\)会等于\(u_1\)这个成分乘上\(c_1\),加上\(u_2\)这个成分乘上\(c_2\),一直加到\(u_k\)这个成分乘上\(c_K\),再加上\(\bar{x}\)(\(\bar{x}\)是所有图像的平均)。所以每一张图像,就是一堆成分的线性组合加上所有图像的平均所组成的。
例如7是\(u^1,u^3,u^5\)加起来的结果,那么对7来说,公式里的\(c_1=1,c_2=0,c_3=1 ...\),所以可以用\(c_1,c_2,...,c_K\)来表示一张图像,如果成分远比像素维度小的话,那么用\(\begin{bmatrix} c_1\\c_2\\ \vdots \\c_K \end{bmatrix}\)表示一张图片是会比较有效的。比如7可以由向量\(\begin{bmatrix} 1 \\0\\1\\0\\1 \\ \vdots \end{bmatrix}\)描述。
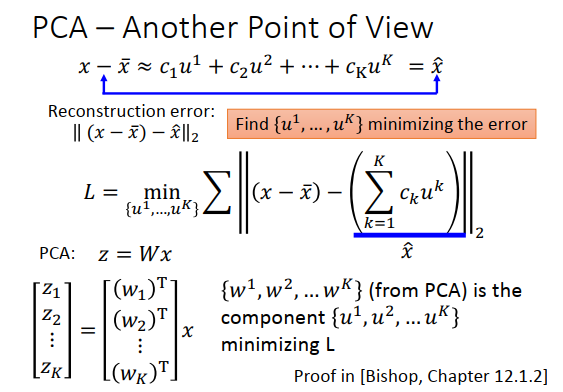
我们把公式里的\(\bar x\)移到左边,\(x\)减\(\bar x\)等于一堆成分的线性组合,写作\(\hat x\) 。
如果我们不知道\(K\)个\(u\)(成分)是什么,那怎么找出这\(K\)个向量?
找\(K\)个\(u\),让\(x-\bar x\)和\(\hat x\)越接近越好,\(||(x-\bar x)-\hat x||_2\)称为重构误差,没办法用成分描述。接下来,最小化\(||(x-\bar x)-\hat x||_2\),损失函数如上图\(L\)。
回忆下PCA,\(w_1,w_2,...,w_K\)是\(x\)协方差矩阵的特征向量,事实上\(L\)的解就是PCA的\(w_1,...,w_K\)。
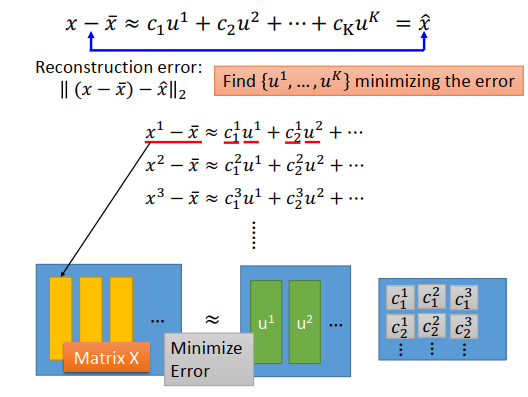
证明\(L\)的解就是PCA的\(w_1,...,w_K\)
现在有数据集\(x\),\(x^1-\bar x \approx c_1^1u^1+c_2^1u^2+...\)。\(x^1-\bar{x}\)是一个向量,\(u^1,u^2...,u^K\)是一排的向量,\(c_1^1,c_2^1...\)也排成一列,最后矩阵形式如上图最下方所示。
左边矩阵\(X\)的列数就是数据数量,有1万笔数据就有一万个列。
目标是最小化左边矩阵\(X\)和右边相乘得到的矩阵。

怎么求解这个最小化问题?
在线性代数里,任何矩阵都可以做奇异值分解,如上图最下方所示。\(K\)就是成分的个数。把\(X\)分解成\(U,\Sigma,V\) ,\(U\)就是上图的最上方的\(u^1,u^2,...\),\(\Sigma V\)就是关于\(c\)的部分。
用奇异值分解的矩阵拆解方法,拆出来的3个矩阵相乘,跟左边矩阵\(X\)是最接近的。\(U\)的K个列是正交的,是\(XX^T\)最大的K个特征值对应的特征向量, 这里的\(XX^T\)就是\(\begin{bmatrix} x^1-\bar x & x^2-\bar x&...&x^K-\bar x \end{bmatrix} \cdot \begin{bmatrix} x^1-\bar x\\x^2-\bar x\\ \vdots \\ x^K-\bar x \end{bmatrix}\),是\(X,X\)的协方差矩阵。
PCA找出来的\(w\)是\(x\)协方差矩阵的特征向量,SVD里\(U\)的每一列都是\(x\)协方差矩阵的特征,其实SVD的\(U\)就是PCA的解。PCA找出来的\(W\)就是在最小化\(X\)和\(U\Sigma V\)的差异,PCA投影得到的其实就是\(\Sigma V\)(也就是上图最上方\(c\)的向量) ,\(W\)就是基本成分。
Autoencoder

我们已经知道从PCA 找出来的\(w^1,w^2,...,w^K\)就是K个成分\(u^1,u^2,...,u^K\)。
我们有个成分线性组合叫做\(\hat x\) ,\(\large \hat x=\sum\limits_{k=1}^kc_kw^k\),我们希望的是\(\hat {x}\)和\(x-\bar x\)的重构误差越小越好。
现在用SVD得到\(W\),那\(c_k\)的值是多少?
每一个样本(如果是图像识别的话,就是每一个图像)都有一组自己的\(c_k\)(\(c_1^1,c_2^1,...\),\(c_1^2,c_2^2,...\)),那么\(c_k\)就各自找就好了。
这个问题其实是问,如果有K个向量(\(w^1,w^2,...,w^K\)),做span以后得到一个空间,这K个向量如何做线性组合,才能使\(\hat x\)最接近于\(x-\bar x\) 。因为K个向量是正交的,所以最好的\(c_k\) 可以直接求解,为\(c_k=(x-\bar x)\cdot w^k\)。
\(w^1,w^2,...,w^K\)做线性组合可以想成是做神经网络。假设\(x-\bar x\)是一个向量,例如上图最下方是一个三维的向量,如果\(K=2\)(两个成分,即向量\(w^1,w^2\),\(w^1=\))。那么计算\(c_1=(x-\bar x)\cdot w^1\)就好像是计算一个神经元一样,\(x-\bar x\)是input,\(w_1^1,w_2^1,w_3^1\)是权重,是线性的神经元,没有激活函数。

\(c_2\)也一样
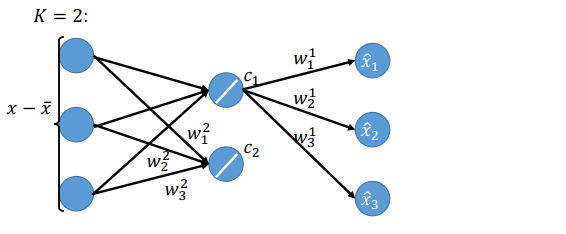
\(c_1\)乘上\(w_1^1\)(\(w_1\)的第一维)得到一个值\(\hat{x_1}\),乘上\(w_2^1\)得到\(\hat {x_2}\),乘上\(w_3^1\)得到\(\hat {x_3}\)
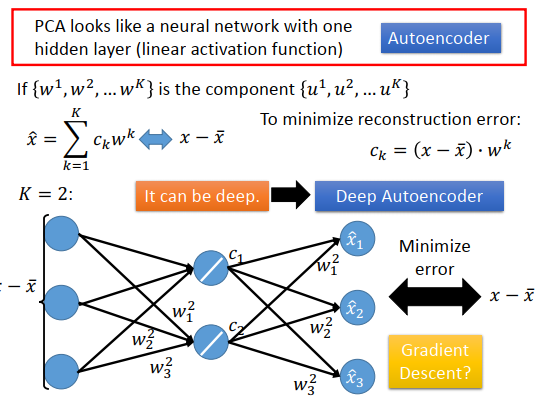
接下来再算\(c_2\)的,乘上\(w_1^2,w_2^2,w_3^2\)得到\(c_2\),再乘以\(w_1^2,w_2^2,w_3^2\)得到三个元素,加到\(c_1\)得到的三个元素上,就是最后的output \(\hat x\)。
我们训练的标准是最小化\(\hat x\)和\(x-\bar x\)的差别,即希望神经网络的output 跟\(x-\bar x\)越接近越好。
那么PCA可以表示成一个神经网络,只有一个激活函数为线性的隐藏层,训练的目标是让output和input越接近越好,这个东西叫做autoencoder(自动编码器)
这里会有一个问题,如果权重\(\{w^1,w^2,...,w^K\}\)不是用PCA的方式(找特征向量的方式),而是使用一个神经网络,最小化error然后使用梯度下降求解,最后得到的结果会跟PCA解出来的\(w\)一样吗?
结果会不一样,PCA解出来的\(w\)是正交的,而使用神经网络得到的\(w\),不能保证一定是正交的。在SVD里面证明过,PCA得到的这组\(w^1,...,w^K\)可以让重构误差最小,但是用神经网络不一定能找出来,不可能让重构误差比PCA找到的还要小。在线性情况下,使用PCA找\(w\)比较快,使用神经网络则比较麻烦。
但是使用神经网络的好处是,可以deep,可以改成有很多个隐藏层,这个就是deep autoencoder。
PCA的缺点

因为PCA是非监督学习,如果有一个未标注数据集,PCA把它们投影到一维上,会找一个让投影数据方差最大的维度,比如上图左上方的case里面,可能维度是斜下方红线这一维。但是可能实际上,这是两组数据集,分别代表了两个类别,使用PCA会导致橙色点和蓝色点结合在一起,投影数据就混合在一起没办法区别。那这时候就要引入标注数据,LDA就是考虑标注数据的降维方法。
另外一个缺点是,PCA是线性的,举的例子会说有一个S型的流形曲面,我们希望做降维后,可以把它拉直,但PCA做不到这件事情。因为把曲面拉直是一个非线性变换,PCA能做的就是把它打扁,如上图右下方所示,从上往下拍扁了,而不是拉开。
PCA实例
宝可梦

有800种宝可梦,每种宝可梦可以用6个特征来表示。所以每个宝可梦就是6维的数据点,6维向量。
现在用PCA来分析,PCA里常有的问题是到底需要几个成分,即到底要把数据降到几维。这个一般取决于你的目的是什么,比如你想做可视化,分析宝可梦特性之间的关系,6为没办法可视化,那就投影到二维。要用几个主成分就好像是神经网络需要几层,每层几个神经元一样。
一个常见决定使用几个主成分的方法是,去计算每个主成分(特征向量)对应的特征值,这个特征值代表在该主成分上投影数据的方差。
现在的例子里宝可梦是6维的,那就有6*6维的协方差矩阵,所以有6个特征值,如上图计算每个特征值比例,结果是0.45,0.18,0.13,0.12,0.07,0.04。那第5、6个主成分的作用比较小,意味着投影数据的方差很小,宝可梦的特性在这两个主成分上信息很少。那么分析宝可梦特性只需要前4个主成分。
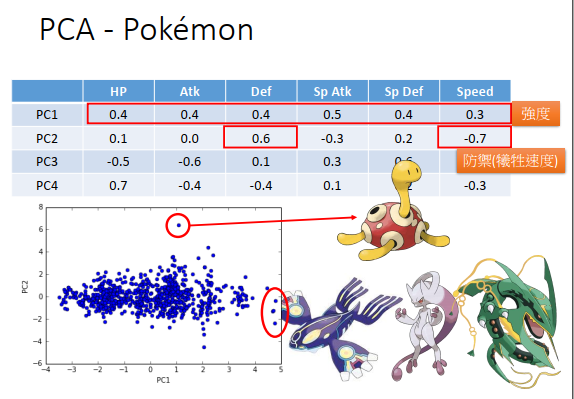
PCA后选择4个主成分,每个主成分是一个6维向量(因为原来每个特征都要投影,那就有6种投影数据)。
每个宝可梦可以想成是4主成分向量做线性组合的结果,且每只宝可梦组合的权重不同。
看第一个主成分PC1,数值都是正的,如果给它的权重大,意味着宝可梦6维都是强的,给它的权重小,意味着宝可梦6维都是弱的,所以第一个主成分,代表了这只宝可梦的强度。
看第二个主成分PC2,Def防御力是正值,速度是负值,那么增加权重的时候,会增加防御力并减小速度。
把第一个和第二个主成分画出来如上图最下方,图上有800个点,每个点代表一只宝可梦。

第三个主成分PC3,特殊防御力是正的,攻击力和HP都是负的,也就是说这是用攻击力和HP来换取特殊防御力的宝可梦。
第四个主成分PC4,HP是正的,攻击力和防御力是负的,这是用攻击力和防御力换取生命值的宝可梦。
把第三、第四主成分画出来如上图最下方,维度是去相关的。
手写数字识别

可以把每一张数字图像拆成成分的线性组合,每一个成分也是一张图像(28 *28 维的向量),所以可以把成分画在图上变成一张图像。
通过PCA画出前30个成分如上图所示,白色的地方代表有笔画。用这些成分做线性组合,就可以得到0-9的数字,所以这些成分叫做Eigen-digit。Eigen(本征)是说,这些成分都是协方差矩阵的特征向量。
人脸识别
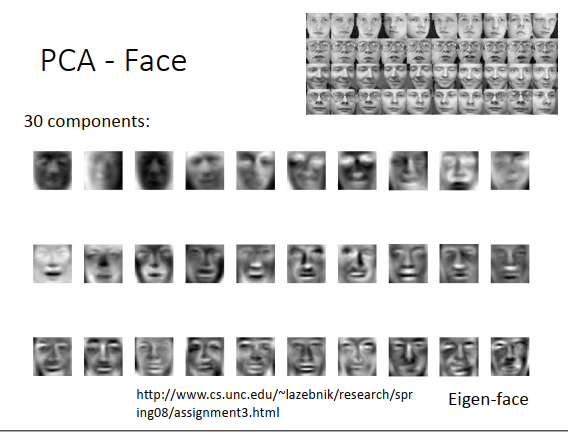
上图右上方有一大堆人脸,找它们前30个主成分。找出来就如上图最下方所示,每张图像都是哀怨的脸,叫做Eigen-face。把这些脸做线性组合,就可以得到所有的脸。

但这边有没有觉得有问题,因为主成分找出来的是成分,但是现在找出来的几乎都是完整的脸,也不像是成分啊?像前面的数字识别,成分看起来也像是玛雅文字,而不是笔画,看起来也不是成分啊?
仔细想想PCA的特性,\(\alpha_1,\alpha_2\)这种权重可以是任何值,可以是正的,也可以是负的。所以当我们用这些主成分组成一张图像的时候,可以把这些成分相加,也可以把这些成分相减,这就会导致你找出的东西不见得是一个图的基本的结构。
比如我画一个9,那可以先画一个8,然后把下面的圈圈减掉,再把一缸加上去。我们不一定是把成分加起来,也可以相减,所以说就可以先画一个很复杂的图,然后再把多余的东西减掉。这些成分不见得就是类似笔画的这种东西。
如果要得到类似笔画的东西,就要用另一个技术NMF(非负矩阵分解)。PCA可以看成是对矩阵\(X\)做SVD,SVD就是一种矩阵分解的技术。如果使用NMF,就会强迫所有成分的权重都是正的,正的好处就是一张图像必须由成分叠加得到,不能说先画一个复杂的东西再去掉一部分,再来就是所有成分的每个维度都必须是正的。

所以在同样的任务上,例如手写数字的测试上,使用NMF时,找出来的主成分会如上图所示。
你会发现,白色图案类似于笔画,找出来的主成分就成了笔画了。

看脸的话,会发现如上图所示。比较像脸的一部分,比如人中、眉毛、嘴唇、下巴。
矩阵分解-推荐系统
有时候,你会有两种东西,两种对象,它们之间受到某种共通的潜在因素操控。
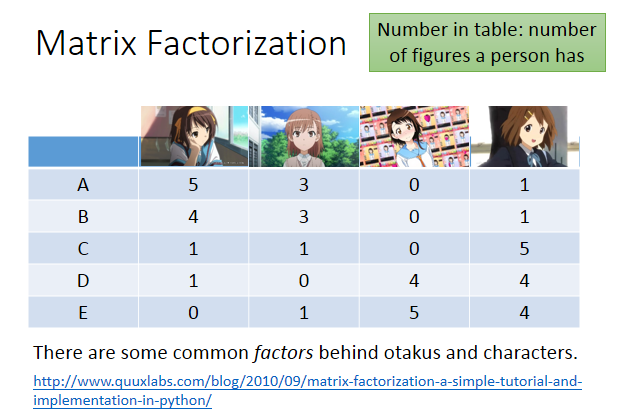
假设现在做一个调查,调查每个人手上买的公仔的数目,A,B,C,D,E代表5个人,公仔人物是凉宫春日、御坂美琴、小野寺、小唯,调查结果如上图。
你会发现在上面矩阵里的数值不是随机出现的,买凉宫春日的人,比较有可能有御坂美琴;买小野寺的人,也比较有可能买小唯。这说明人和公仔有一些共同的特性,有共同的factor在操控这些事情发生。
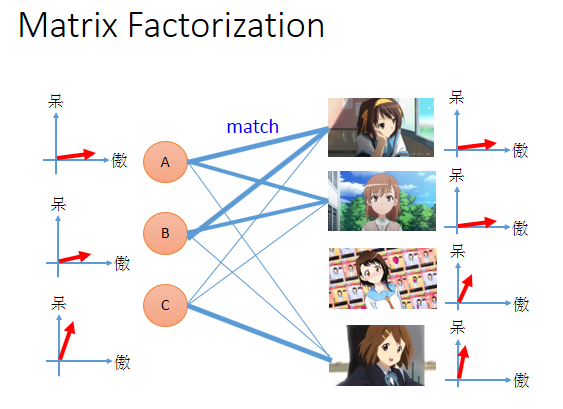
动漫宅获取可以分成两种,一种是萌傲娇的,一种萌天然呆的。每个人都是萌傲娇和萌天然呆平面上的一个点,可以用一个向量表示,那么看上图,A是偏萌傲娇。每一个公仔角色,可能有傲娇属性或者天然呆属性,所以每一个角色,也是平面上一个点,可以用一个向量描述。
如果某个人的属性和角色的属性匹配的话,他们背后的向量就很像(比如做内积的时候值很大),那么A就会买很多的凉宫春日。他们匹配的程度取决于潜在因素是不是匹配的。
所以ABC的属性如上图最左边所示,A、B是萌傲娇的,B稍微没有那么傲娇,C是萌天然呆。每个动漫角色后面也有傲娇、天然呆这两种属性,如果人物属性和角色属性匹配的话,人买角色的可能性就很大。
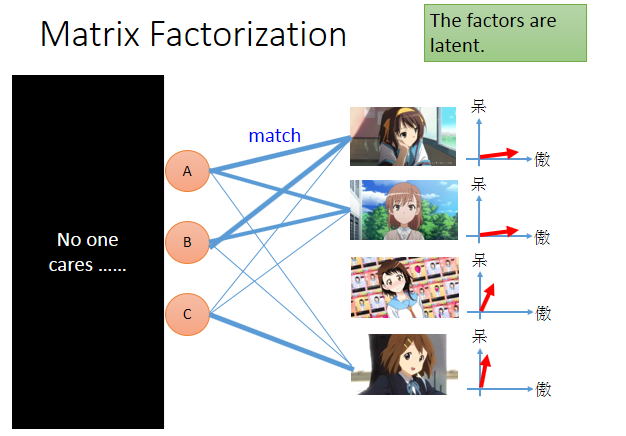
但是傲娇还是天然呆是潜在因素,没有办法直接被观察。没有人在意一个阿宅心里在想什么。也没有办法直接知道每一个动漫角色背后的属性是什么。

我们知道的只有人买的角色的数目,然后凭着这种关系去推论每个人和每个动漫人物背后的潜在因素。每个人背后都有一个向量,代表萌傲娇或者萌天然呆的程度。每个角色后面也有一个序列,代表是傲娇或天然呆的属性。
我们可以把购买的公仔数量合起来看做是一个矩阵\(X\) ,行数是人的数量,列数是公仔角色的数量。
现在有一个假设,矩阵\(X\)里的每个元素都来自于两个向量的内积。为什么A会有5个凉宫春日的公仔,是因为\(r^A\cdot r^1\)的内积很大,约等于5。这件事情用数学公式表达的话,可以把\(r^A\)到\(r^M\)按列排起来,把\(r^1\)到\(r^4\)按行排起来,K是潜在因素的个数,一般没办法知道,需要自己测试出来。
上图中右下方矩阵公式中,右边两个矩阵的N应该是M,代表M个人。
矩阵\(X\)的每个维度是什么?
比如最上角维度\(n_{A1}\)就是\(r^A \cdot r^1\),那么就是公仔数目的矩阵。
我们要做的事情就是找一组\(r^A\)到\(r^E\),找一组\(r^1\)到\(r^4\) ,让两个矩阵相乘后和矩阵\(X\)越接近越好,就是最小化重构误差。这个就可以用SVD来解,把\(\Sigma\)并到左边或右边变成两个矩阵就可以了。

有时候有些信息是缺失的,比如上图所示的,你不知道ABC手上有没有小野寺,可能在那个地区没有发行,所以不知道发行的话到底会不会买。那用SVD就很怪,也可以把缺失值用0代替,但也很奇怪。
那有缺失值怎么办呢?
可以用梯度下降的方法来做,写一个损失函数,让\(r^i\)(每个人背后的潜在因素)和\(r^j\)(角色背后的潜在因素)的内积和角色购买数量越接近越好。现在重点是,在summation over 元素的时候,可以避开缺失的数据,如果值是缺失的,就不计算。有了损失函数后,就可以使用梯度下降了。
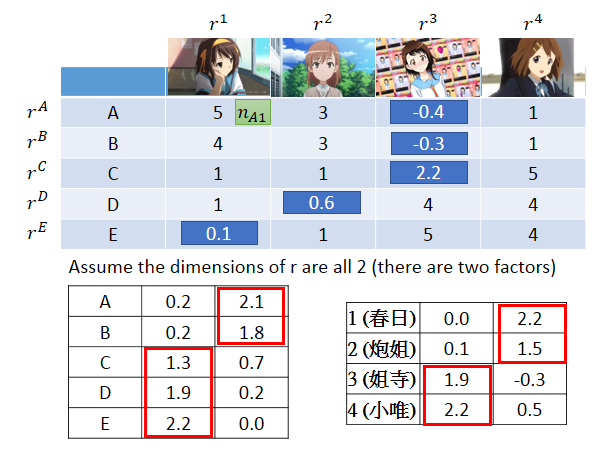
根据刚才的方法实际计算一下,假设潜在因素的数量是2。那么\(A\)到\(E\)都是二维的向量,每个角色也是二维的向量。
数值代表了属性的程度,把大的用红色框框圈出来,会发现\(A、B\)萌同一组属性,\(C、D、E\)萌同一种属性,1,2有同样的属性,3,4有同样的属性。没有办法知道每个属性代表什么,要先找出这些潜在因素,再去分析它的结果。有了这些潜在因素数据,就可以用来预测缺失值。已经知道了\(r^A\)和\(r^3\),那只要\(r^A\)和\(r^3\)做内积就可以了。

之前的model可以做得更精致一点,刚才说\(A\)背后的潜在因素乘上1背后的潜在因素,得到的结果就是矩阵里的数值。但是事实上,可能还会有其他因素操控这些数值。那么更精确的写法就可以写成\(r^A \cdot r^1+b_A+b_1 \approx 5\)。\(b_A\)是跟\(A\)有关的标量,代表了\(A\)有多喜欢买公仔,有的人就是喜欢买公仔,也不是喜欢某个角色。\(b_1\)是跟1有关的标量,代表了角色有多想让人购买,这个事情是跟属性无关的,本来人就会买这个角色。
然后修改损失函数如上图所示,使用梯度下降求解即可。
矩阵分解-其他应用

矩阵分解还有其他的应用,比如可以用在主题分析上,把矩阵分解用在主题分析上,叫做LSA。技术是一样的,把动漫角色换成文章,把人换成词汇即可,table里的值就是词频。比如投资这个词汇在Doc1里出现5次。有时候不只是用词频,会把词频乘上一个权重,代表词本身有多重要,乘一个大的权重,就会更考虑这个词,让这个词的重构误差变得更小。
那怎么评估一个词重不重要?
有很多方法,常用的有inverse document frequency(反文档频率)IDF。