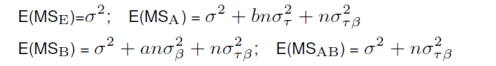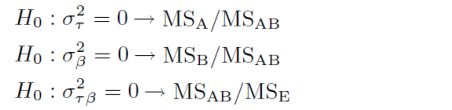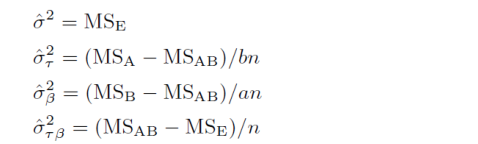UA MATH571B 试验设计VI 随机效应与混合效应1

现在回到试验设计III 单因素试验设计1中介绍的模型， $y_{ij} = \mu + \tau_i + \epsilon_{ij},\epsilon_{ij}\sim_{iid}N(0,\sigma^2)\\ i = 1,2,\cdots,a; j=1,2,\cdots,n$

其中 $\mu$是总体均值（grand mean）， $\tau_i$是第 $i$种factor level的treatment effect， $\mu_i=\mu+\tau_i$，这个模型叫效应模型（effect model）。我们想研究的是单个treatment factor的不同level对response的影响。用最小二乘法估计这个模型的时候，我们得到的方程是
$an\hat{\mu}+\sum_{i=1}^a \hat{\tau}_i=y_{..}\\n\hat{\mu}+ n\hat{\tau}_i=y_{i.},i=1,\cdots,a$

线性独立的方程只有 $a$个，但要估计的系数有 $a+1$个，因此我们为了估计系数引入了一个假设：
$\sum_{i=1}^a \hat{\tau}_i = 0$

并称满足这个方程的factor为fixed factor。引入这个假设意味着我们认为treatment factor的level是人为设计，并且包含了treatment factor的绝大多数可能性，这样的因素模型我们称之为固定效应模型。固定效应模型中缺一个方程的原因是总体均值与treatment effec的线性相关性，除了增加额外的约束外，还可以考虑增加模型的随机性。固定模型要求穷尽treatment factor所有取值是可能实现的，那么当treatment factor有非常多的可能的值时，样本中的treatment factor level其实是对level的population的抽样，treatment effect也就不会是固定的，而是与treatment factor level一样是随机的。称factor level和factor effect是随机变量的factor为random factor，只含有random factor的模型为随机效应模型；同时含有random factor与fixed factor的模型为混合效应模型。

两个factor的随机效应模型

假设我们关注A和B两个factor的effects，它们都是random factors，模型设定为：
$y_{ijk} = \mu + \tau_i + \beta_j +(\tau \beta)_{ij}+ \epsilon_{ijk}\\ \epsilon_{ijk} \sim_{iid}N(0,\sigma^2);i=1,\cdots,a;j=1,\cdots,b;k=1,\cdots,n \\ \tau_i \sim_{iid} N(0,\sigma_{\tau}^2),\beta_j \sim_{iid} N(0,\sigma^2_{\beta}),(\tau \beta)_{ij} \sim_{iid} N(0,\sigma_{\tau \beta}^2)$

从而方差分解为：
$Var(y_{ijk}) = \sigma^2_{\tau} + \sigma^2_{\beta} + \sigma^2_{\tau \beta} + \sigma^2$

因素模型中我们讨论的最基本的问题永远是某个因素对试验结果是否存在显著的效应，具体表现为在总体均值以外，因素的不同水平是否会造成试验结果的显著区别。在固定效应模型中，我们比较的方式是用ANOVA做多组level的effect均值的检验，比较他们是否同时显著为0；在随机效应模型中，不同level的effect相同则意味着factor effect的方差为0，因此随机效应模型中我们需要做的检验是：
$H_0:\sigma_{\tau}^2=0 \\ H_0:\sigma_{\beta}^2=0\\ H_0:\sigma_{\tau \beta}^2=0$

接下来，我们要试图修正之前一直在用的ANOVA分析框架使之能够用在随机效应模型中。先定义几个符号：
$y_{i..} = \sum_{j=1}^b\sum_{k=1}^n y_{ijk}, \bar{y}_{i..} = \frac{y_{i..}}{an} \\ y_{.j.} = \sum_{i=1}^a \sum_{k=1}^n y_{ijk}, \bar{y}_{.j.} = \frac{y_{.j.}}{bn} \\ y_{ij.} = \sum_{k=1}^n y_{ijk}, \bar{y}_{ij.} = \frac{y_{ij.}}{n}\\ y_{...} = \sum_{i=1}^a y_{i..}=\sum_{j=1}^b y_{.j.}, \bar{y}_{...} = \frac{y_{...}}{N},N=abn$

考虑平方和分解，总平方和为：
$SST = \sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (y_{ijk}-\bar{y}_{...})^2$

做一个替换
$y_{ijk} - \bar{y}_{...} = (\bar{y}_{i..}-\bar{y}_{...}) + (\bar{y}_{.j.}-\bar{y}_{...}) + (\bar{y}_{ij.}-\bar{y}_{i..} -\bar{y}_{.j.} + \bar{y}_{...} ) + (y_{ijk} - \bar{y}_{ij.})$

可以自行验证下面的结果：
$SST = bn \sum_{i=1}^n(\bar{y}_{i..}-\bar{y}_{...})^2 + an\sum_{j=1}^b(\bar{y}_{.j.}-\bar{y}_{...})^2 + n\sum_{i=1}^a\sum_{j=1}^b (\bar{y}_{ij.}-\bar{y}_{i..} -\bar{y}_{.j.} + \bar{y}_{...} )^2 +\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n (y_{ijk} - \bar{y}_{ij.})^2$

定义等式右边的平方和为 $SS_A,SS_B,SS_{AB},SSE$，则平方和分解为
$SST = SS_A + SS_B + SS_{AB} + SSE$

总平方和的自由度为 $df_T = N-1$， $SS_A$的自由度为 $df_A = a-1$， $SS_B$的自由度为 $df_B = b-1$， $SS_{AB}$的表达式中包含的约束为
$\sum_{j=1}^b \bar{y}_{ij.} = b\bar{y}_{i..},i=1,\cdots,a; \sum_{i=1}^a \bar{y}_{ij.} = a\bar{y}_{.j.},j=1,\cdots,b; n\bar{y}_{...} = \sum_{i=1}^a y_{i..}=\sum_{j=1}^b y_{.j.}$

自由方程数目为 $a+b-1$，因此
$df_{AB} = ab - a - b + 1 = (a-1)(b-1) \\ df_{Model} = df_{A} + df_{B} + df_{AB} = ab - 1$

所以残差的自由度为
$df_E = df_T - df_{Model} = abn - ab = ab(n-1)$

根据平方和与自由度可以定义均方和，下面是一些常用结果，可以自行验证：

以上是ANOVA方法在随机效应模型上的修正，ANOVA方法中主要用的估计量是最小二乘估计（其实也是矩估计）；另一种估计方差的方法是最大似然估计，在随机效应与混合效应模型中使用的最大似然估计称为residual maximum likelihood (REML)模型，与ANOVA不同的是，ANOVA直接得到的是平方和的分解，而REML直接得到的是方差的估计，因此REML在计算方差的置信区间、做方差的假设检验等方面更便捷。