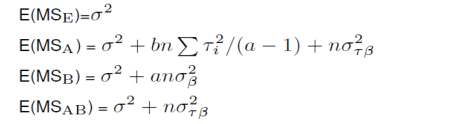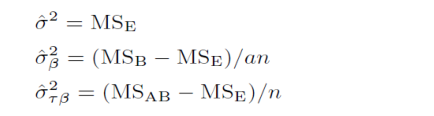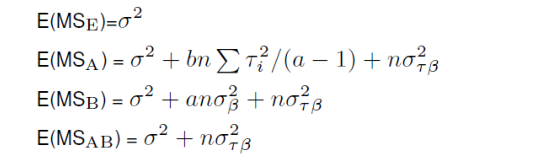UA MATH571B 试验设计VI 随机效应与混合效应2

两个factor的混合效应模型

假设我们关注A和B两个factor的effects，但A是fixed factor，B是random factor，模型设定为：
$y_{ijk} = \mu + \tau_i + \beta_j +(\tau \beta)_{ij}+ \epsilon_{ijk}\\ \epsilon_{ijk} \sim_{iid}N(0,\sigma^2);i=1,\cdots,a;j=1,\cdots,b;k=1,\cdots,n \\ \sum_{i=1}^a \tau_i = 0,\beta_j \sim_{iid} N(0,\sigma^2_{\beta})$

因为A是fixed factor，所以A的treatment effect $\tau_i$满足fixed effect的约束；B是random factor，所以B的treatment effect $\beta_j$是随机变量。难点在于交互效应 $(\tau \beta)_{ij}$的处理，交互的两个factor一个是fixed factor，另一个是random factor，这非常自然地引出了两种不同的观点：1）因为交互效应的产生有random factor的作用，所以应该把交互效应当做随机变量（Unrestricted Mixed Model）；2）交互效应中来自fixed factor的部分同样应该加上fixed effect的约束（Restricted Model）。

Restricted Model

交互效应中来自fixed factor的部分应该满足约束：
$\sum_{i=1}^a (\tau \beta)_{ij} =(\tau \beta)_{.j} = 0,\forall j$

但是因为random factor的存在，交互效应还是随机的，不存在约束的时候，交互效应满足：
$(\tau \beta)_{ij} \sim_{iid} N(0,\sigma_{\tau \beta}^2)$

因为约束的存在，自由度应该减1，上面的分布应该修正为
$(\tau \beta)_{ij} \sim N(0,\frac{a-1}{a}\sigma_{\tau \beta}^2)$

并且fixed factor与相同random factor level交互产生的效应不是独立的，
$Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}) = Cov((\tau \beta)_{ij},-\sum_{l=1,\ l \ne i'}^a(\tau \beta)_{lj})$

在 $l=1,\cdots,a,l \ne i'$中，
$Cov((\tau \beta)_{ij},(\tau \beta)_{ij}) = Var((\tau \beta)_{ij}) =\frac{a-1}{a} \sigma_{\tau \beta}^2, l = i \\ Cov((\tau \beta)_{ij},(\tau \beta)_{lj})=Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}),l=1,\cdots,a,l \ne i',i$

因此
$Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}) = -\frac{a-1}{a}\sigma_{\tau \beta}^2 - (a-2)Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}) \\ \Rightarrow Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}) = -\frac{1}{a}\sigma_{\tau \beta}^2$

综上，Restricted Model关于交互项有3条假设：

1. $\sum_{i=1}^a (\tau \beta)_{ij} =(\tau \beta)_{.j} = 0,\forall j$
2. $(\tau \beta)_{ij} \sim N(0,\frac{a-1}{a}\sigma_{\tau \beta}^2),\ Cov((\tau \beta)_{ij},(\tau \beta)_{i'j}) = -\frac{1}{a}\sigma_{\tau \beta}^2,\forall j$（协方差这条是1和2的前半句导出的）
3. fixed factor与不同random factor level交互产生的效应是独立的

这个模型有如下结果：

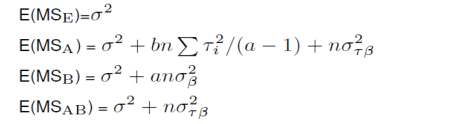
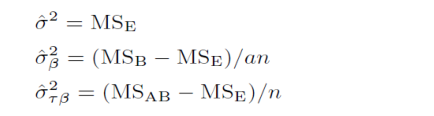
Unrestricted Mixed Model

Unrestricted Mixed Model对交互项的处理与两因素的随机效应模型是一样的，假设
$(\tau \beta)_{ij} \sim_{iid} N(0,\sigma_{\tau \beta}^2)$

这个模型的部分结果如下：

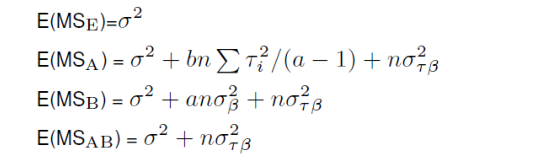
注意到B的均方和的期望中包含了残差、B的treatment effect，交互项三部分的方差，因此检验因素B的方差是否为0时F统计量要用 $MS_B/MS_{AB}$而不是 $MS_B/MS_E$！

事实上Unrestricted Mixed Model可以化归为Restricted Model。定义
$(\bar{\tau} \beta)_{.j} = \frac{1}{a}\sum_{i=1}^a (\tau \beta)_{ij}$

对Unrestricted Mixed Model做简单变形：
$y_{ijk} = \mu + \tau_i + \beta_j +(\tau \beta)_{ij}+ \epsilon_{ijk} \\ = \mu + \tau_i + (\beta_j +(\bar{\tau} \beta)_{.j}) +((\tau \beta)_{ij} - (\bar{\tau} \beta)_{.j})+ \epsilon_{ij}$

定义 $\gamma_j = \beta_j +(\bar{\tau} \beta)_{.j},\ (\tau \gamma)_{ij} = (\tau \beta)_{ij} - (\bar{\tau} \beta)_{.j}$，验证以下模型是Restricted Model：
$y_{ijk} = \mu + \tau_i + \gamma_j +(\tau \gamma)_{ij} + \epsilon_{ijk}$

计算
$\sum_{i=1}^a (\tau \gamma)_{ij} = \sum_{i=1}^a[ (\tau \beta)_{ij} - (\bar{\tau} \beta)_{.j}] = \sum_{i=1}^a (\tau \beta)_{ij} -a(\bar{\tau} \beta)_{.j}=0 \\ Cov((\tau \gamma)_{ij},(\tau \gamma)_{ij}) = Cov((\tau \beta)_{ij} - (\bar{\tau} \beta)_{.j},(\tau \beta)_{ij} - (\bar{\tau} \beta)_{.j}) \\ = \sigma^2_{\tau \beta} - \frac{1}{a} \sigma^2_{\tau \beta} - \frac{1}{a} \sigma^2_{\tau \beta} + \sum_{i=1}^a \frac{1}{a^2}\sigma^2_{\tau \beta} = \frac{a-1}{a}\sigma^2_{\tau \beta}$

因此Restricted Model比Unrestricted Mixed Model更具有一般性。

对两因素随机与混合效应模型的总结

这是我老师课件上的表格，感觉总结得不错，贴在这里：

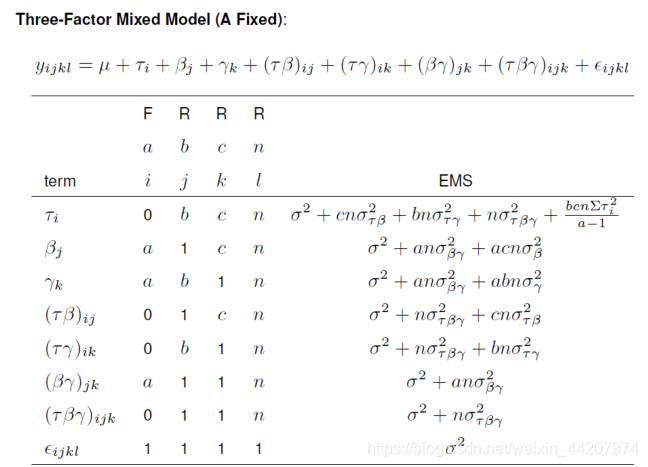
注意这些表展示的都是ANOVA方法的框架，EMS表示均方和的期望，根据均方和的期望可以把F统计量写出来，比如最后这张表，要检验 $H_0:\sigma^2_{\beta}=0$需要用它对应的均方和除以 $(\beta \gamma)$对应的均方和，因为它对应的EMS里面包含残差、 $(\beta \gamma)$以及 $\beta$三部分方差，要检验 $\beta$的需要剔除前两项，对应的就是 $(\beta \gamma)$的EMS。

同样以最后这张表为例，表格上半部分第一行表示某个指标适用固定效应（F）还是随机效应（R）的假设；第三行是指标的记号；第二行表示指标的最大取值。表格下半部分第一列是不同的effect，比如 $\tau_i$关于 $i$指标是0说明它服从固定效应的假设，关于后面三个指标都是对应指标的最大值，说明 $\tau_i$与后面三个指标无关； $\beta_j$关于指标 $j$是1说明它服从随机效应的假设，关于另外三个指标都是对应指标的最大值说明它与另外三个指标无关； $(\tau \beta)_{ij}$关于关于 $i$指标是0，关于指标 $j$是1，说明它适用Restricted Model的假设。