UA MATH567 高维统计IV Lipschitz组合11 社区发现 Spectral Clustering容许的最大随机噪声
社区发现的Spectral Clustering算法复习
我们在上一部分介绍随机矩阵的时候介绍了stochastic blocking model以及community detection的spectral clustering算法。
假设这个网络有 n n n个节点,网络中有两个社区,它们的规模相当,各拥有 n / 2 n/2 n/2个节点,记这两个社区为 C 1 , C 2 C_1,C_2 C1,C2,我们用 G ( n , p , q ) G(n,p,q) G(n,p,q)表示这个随机网络,其中 p p p表示某条边连接的两个点属于同一个社区的概率, q q q表示某条边连接的两个点属于不同社区的概率,假设 p > q p>q p>q,用 A A A表示这个网络的伴随矩阵,显然它是一个随机矩阵,
P ( A i j = 1 ∣ i , j ∈ C 1 o r i , j ∈ C 2 ) = p P ( A i j = 1 ∣ i ∈ C 1 , j ∈ C 2 o r i ∈ C 2 , j ∈ C 1 ) = q P(A_{ij}=1|i,j \in C_1\ or\ i,j \in C_2)=p \\ P(A_{ij}=1|i \in C_1,j \in C_2\ or\ i \in C_2,j \in C_1)=q P(Aij=1∣i,j∈C1 or i,j∈C2)=pP(Aij=1∣i∈C1,j∈C2 or i∈C2,j∈C1)=q
我们可以将 A A A分解为它的期望与残差矩阵:
A = E [ A ] + R A = E[A]+R A=E[A]+R
Community detection in networks的目标是给定一个某个随机矩阵的样本数据集,要还原随机矩阵的期望的特征向量,下面是Spectral clustering的算法描述:

我们在上部分第八讲用Davis-Kahan定理说明了它的理论性质:考虑随机网络 G ( n , p , q ) G(n,p,q) G(n,p,q),如果 min ( q , p − q ) = μ > 0 \min(q,p-q)=\mu>0 min(q,p−q)=μ>0,则 ∃ c > 0 \exists c>0 ∃c>0,Spectral Clustering最多搞错 c / μ 2 c/\mu^2 c/μ2个节点的概率至少是 1 − 4 e − n 1-4e^{-n} 1−4e−n。这个结论的条件是
∥ D ∥ ∼ n , P ( ∥ R ∥ = O ( n ) ) ≥ 1 − 4 e − n \left\| D\right\| \sim n,P(\left\| R \right\| =O(\sqrt{n})) \ge 1-4e^{-n} ∥D∥∼n,P(∥R∥=O(n))≥1−4e−n
用矩阵Bernstein不等式推导Spectral Clustering的理论性质
注意到 ∥ D ∥ = ( p + q ) n / 2 ≥ μ n \left\| D\right\|=(p+q)n/2 \ge \mu n ∥D∥=(p+q)n/2≥μn,所以之前得到的结果需要的条件是
μ n > > O ( n ) \mu n >> O(\sqrt{n}) μn>>O(n)
也就是 ∥ D ∥ > > n \left\| D\right\|>>n ∥D∥>>n,但是用矩阵Bernstein不等式,我们可以把这个条件弱化为 ∥ D ∥ > > log n \left\| D\right\|>>\log n ∥D∥>>logn。
记 d = ∥ D ∥ d=\left\| D\right\| d=∥D∥,定义 A = ∑ 1 ≤ i < j ≤ n Z i j A = \sum_{1 \le i< j \le n}Z_{ij} A=∑1≤i<j≤nZij,其中 Z i j Z_{ij} Zij是 n × n n \times n n×n的矩阵,除了 ( i , j ) (i,j) (i,j)与 ( j , i ) (j,i) (j,i)这两个位置为Bernoulli变量外,其他位置均为0,我们可以说明
E ∥ R ∥ = E ∥ A − E A ∥ ≲ d log n + log n E \left\| R \right\| = E \left\| A - EA \right\| \lesssim \sqrt{d \log n}+\log n E∥R∥=E∥A−EA∥≲dlogn+logn
证明思路
R = A − E A = ∑ 1 ≤ i < j ≤ n ( Z i j − E Z i j ) R = A - EA = \sum_{1 \le i< j \le n}(Z_{ij}-EZ_{ij}) R=A−EA=1≤i<j≤n∑(Zij−EZij)
这里的 Z i j − E Z i j Z_{ij}-EZ_{ij} Zij−EZij是有界(算子范数小于1)、独立、零均值、对称的随机变量,计算
σ 2 = ∥ ∑ E ( Z i j − E Z i j ) 2 ∥ ≈ d \sigma^2 = \left\| \sum E(Z_{ij}-EZ_{ij})^2 \right\| \approx d σ2=∥∥∥∑E(Zij−EZij)2∥∥∥≈d
根据矩阵Bernstein不等式的推论
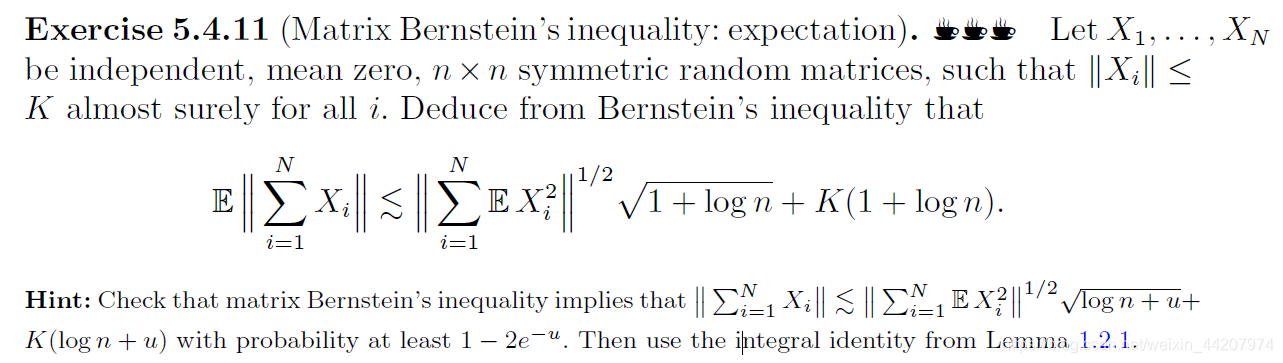
E ∥ R ∥ ≲ σ log n + log n E \left\| R \right\| \lesssim \sigma\sqrt{\log n}+\log n E∥R∥≲σlogn+logn