UA MATH567 高维统计 专题0 为什么需要高维统计理论？——以线性判别分析为例

线性判别分析基础

理论

我们回顾一下二元假设检验问题，它的目标是判断某一个observation $x\in {\mathbb{R}}^d$到底属于总体$P_1$还是$P_2$，在统计理论中，Neyman-Pearson引理说明了似然比检验是最优检验，也就是基于$\log \frac{P_2(x)}{P_1(x)}$导出的检验统计量与拒绝域是最优的。现在我们考虑线性判别分析的设定，假设两个总体分别是$N({\mu }_1,\Sigma ),N({\mu }_2,\Sigma )$，则给定某个observation $x\in {\mathbb{R}}^d$，对数似然比为（多元正态分布的概率密度参考我之前这一篇）
$$\begin{gathered} \log \frac{P_1(x)}{P_2(x)}=\log \frac{(2\pi {)}^{-d/2}|\Sigma {|}^{-1/2}\exp \left(-\frac{1}{2}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}(x-{\mu }_1)\right)}{(2\pi {)}^{-d/2}|\Sigma {|}^{-1/2}\exp \left(-\frac{1}{2}(x-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-{\mu }_2)\right)} \\ =\frac{1}{2}(x-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-{\mu }_2)-\frac{1}{2}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}(x-{\mu }_1) \\ =\frac{1}{2}(x-{\mu }_1+({\mu }_1-{\mu }_2){)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2}+\frac{{\mu }_1+{\mu }_2}{2}-{\mu }_2) \\ -\frac{1}{2}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2}+\frac{{\mu }_1+{\mu }_2}{2}-{\mu }_1) \\ =\frac{1}{2}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2})+\frac{1}{2}({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2}) \\ +\frac{1}{4}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}({\mu }_1-{\mu }_2)+\frac{1}{4}({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}({\mu }_1-{\mu }_2) \\ -\frac{1}{2}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2})-\frac{1}{4}(x-{\mu }_1{)}^{\prime }{\Sigma }^{-1}({\mu }_1-{\mu }_2) \\ =\frac{1}{2}({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2})+\frac{1}{4}({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}({\mu }_1-{\mu }_2) \\ \propto \Psi (x)=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2}) \end{gathered}$$

如果$\Psi (x)>0$，我们认为$x$是来自$P_1$的样本；如果$\Psi (x)\le 0$，我们认为$x$是来自$P_2$的样本；所以判别分析出错的概率是
$$Err(\Psi )=\frac{1}{2}{P}_1[\Psi (x)\le 0]+\frac{1}{2}{P}_2[\Psi (x)>0]$$

定义
$$\gamma =\sqrt{({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}({\mu }_1-{\mu }_2)}$$

先计算第一个概率，如果$x\sim N({\mu }_1,\Sigma )$，则
$$\begin{gathered} E\Psi (x)=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}({\mu }_1-\frac{{\mu }_1+{\mu }_2}{2})=\frac{{\gamma }^2}{2} \\ Var(\Psi (x))=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}\Sigma {\Sigma }^{-1}({\mu }_1-{\mu }_2)={\gamma }^2 \end{gathered}$$

所以$\Psi (x){|}_{P_1}\sim N(\gamma /2,\gamma )$，于是
$$P_1[\Psi (x)\le 0]=P_1(\frac{\Psi (x)-\frac{{\gamma }^2}{2}}{\gamma }\le -\frac{\gamma }{2})=\Phi (-\gamma /2)$$

接下来计算第二个概率，如果$x\sim N({\mu }_2,\Sigma )$，则
$$\begin{gathered} E\Psi (x)=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}({\mu }_2-\frac{{\mu }_1+{\mu }_2}{2})=-\frac{{\gamma }^2}{2} \\ Var(\Psi (x))=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}\Sigma {\Sigma }^{-1}({\mu }_1-{\mu }_2)={\gamma }^2 \end{gathered}$$

所以$\Psi (x){|}_{P_2}\sim N(\gamma /2,\gamma )$，于是
$$P_2[\Psi (x)\le 0]=P_2(\frac{\Psi (x)+\frac{{\gamma }^2}{2}}{\gamma }>\frac{\gamma }{2})=\Phi (-\gamma /2)$$

综上，
$$Err(\Psi )=\Phi (-\gamma /2)$$

算法

我们看一下理论部分的判别规则：如果$\Psi (x)>0$，我们认为$x$是来自$P_1$的样本；如果$\Psi (x)\le 0$，我们认为$x$是来自$P_2$的样本；要使用这个规则进行判别，我们需要计算出
$$\Psi (x)=({\mu }_1-{\mu }_2{)}^{\prime }{\Sigma }^{-1}(x-\frac{{\mu }_1+{\mu }_2}{2})$$

为此，我们需要样本均值与协方差矩阵的估计。假设我们有$n_1+n_2$个样本，前$n_1$个来自总体$P_1$，后$n_2$个来自总体$P_2$，引入样本均值
$${\hat{\mu }}_1=\frac{1}{n_1}\sum _{i=1}^{n_1}{x}_i,{\hat{\mu }}_2=\frac{1}{n_2}\sum _{i=n_1+1}^{n_1+n_2}{x}_i$$

Pooled sample covariance matrix，
$$\hat{\Sigma }=\frac{{\sum }_{i=1}^{n_1}(x_i-{\hat{\mu }}_1)(x_i-{\hat{\mu }}_1{)}^T+{\sum }_{i=1}^{n_2}(x_i-{\hat{\mu }}_2)(x_i-{\hat{\mu }}_2{)}^T}{n_1+n_2-2}$$

把这三个估计量代入$\Psi (x)$，我们就可以得到Fisher线性判别函数(Fisher linear determinant function)：
$$\hat{\Psi }(x)=({\hat{\mu }}_1-{\hat{\mu }}_2{)}^{\prime }{\hat{\Sigma }}^{-1}(x-\frac{{\hat{\mu }}_1+{\hat{\mu }}_2}{2})$$

基于Fisher线性判别函数的判别错误概率为
$$Err(\hat{\Psi })=\frac{1}{2}{P}_1[\hat{\Psi }(x)\le 0]+\frac{1}{2}{P}_2[\hat{\Psi }(x)>0]$$

一个重要的问题是，基于Fisher线性判别函数的判别错误概率能不能等于判别分析出错的理论概率，或者说只比判别分析出错的理论概率大一点点？概统祖师爷Kolmogorov分析过这个问题，如果$d/n_i\to \alpha ,\forall i=1,2$，${\Vert {\hat{\mu }}_1-{\hat{\mu }}_2\Vert }_2{\to }_p\gamma$，协方差矩阵为单位阵，则
$$Err(\hat{\Psi }){\to }_p\Phi (-\frac{{\gamma }^2}{2\sqrt{{\gamma }^2+{\alpha }^2}})$$

我们来简单看一下下面的实证结果：

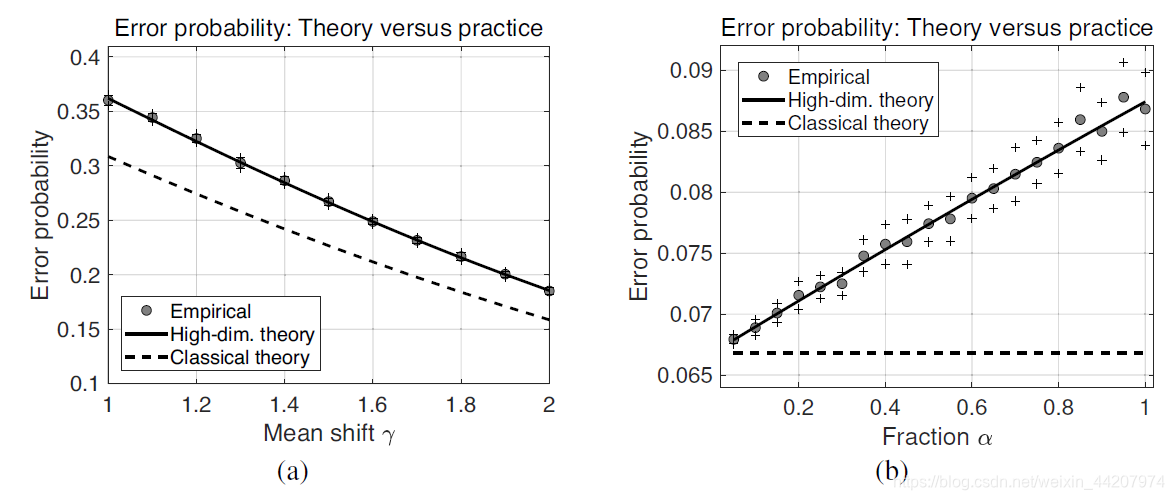
左图：Mean shrift越大，说明这两个总体分得越开，越不容易判别出错；实验结果略大于理论结果，所以还是比较可信的；

右图：$\alpha$越大说明$d/n_i$越大，也就是这个问题的维度越高，这时实验的结果就会越差，但经典理论的结果是不变，因此我们需要建立新的理论来解释高维统计问题。