数学建模--插值算法（SciPy实现）

写在前面：
笔记为自行整理，内容出自课程《数学建模学习交流》，主讲人：清风

一维插值问题

问题如下：已经有 $n+1$ 个节点 $(x_i,y_i)(i=0,1,...,n)$ ，其中 $x_i$ 互不相同，不妨设 $a=x_0<x_1<...<x_n=b$ ，求任意插值点 $x^*({\ne}x_i)$ 处的值 $y^*$ 。
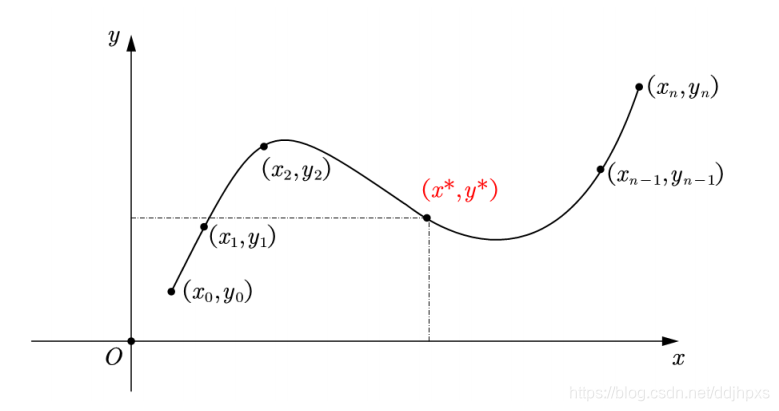
在这里插入图片描述
思路：构造函数 $y=f(x)$ ，使得 $f(x)$ 经过所有节点，求 $f(x^*)$ 即可得到 $y^*$ 。
关键：定义插值函数

插值法原理

**定理：**设有 $n+1$ 个互不相同的节点 $(x_i,y_i)(i=0,1,...,n)$ ，则存在唯一的多项式：
$L_n(x)=a_0+a_1x+a_2x^2+...+a_nx^n$
使得 $L_n(x_j)=y_j (j=0,1,2,...,n)$
注：只要 $n+1$ 个节点互异，则满足上述插值条件的多项式是唯一存在的；
如果不限制多项式的次数，那么插值多项式并不唯一。

拉格朗日插值法

在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。
设有两个点 $(x_0,y_0),(x_1,y_1)$ :
$f\left( x \right) =\frac{x-x_1}{x_0-x_1}y_0+\frac{x-x_0}{x_1-x_0}y_1$
三个点 $(x_0,y_0),(x_1,y_1),(x_2,y_2)$ :
$f\left( x \right) =\frac{\left( x-x_1 \right) \left( x-x_2 \right)}{\left( x_0-x_1 \right) \left( x_0-x_2 \right)}y_0+\frac{\left( x-x_0 \right) \left( x-x_2 \right)}{\left( x_1-x_0 \right) \left( x_1-x_2 \right)}y_1+\frac{\left( x-x_0 \right) \left( x-x_1 \right)}{\left( x_2-x_0 \right) \left( x_2-x_1 \right)}y_2$
需注意：插值多项式并不是次数越高误差越小，高次插值会产生龙格现象，即在两端处波动极大。因此在不熟悉曲线运动趋势的前提下，不要轻易使用高次插值。

分段插值

分段线性插值
在这里插入图片描述
分段二次插值
选取根节点 $x$ 最接近的三个节点，构造一个二次函数，然后进行插值。

分段三次埃尔米特(Hermite)插值

埃尔米特插值原理：
设在区间 $[a,b]$ 上有 $n+1$ 个互异的节点，定义函数 $f(x)$ 在节点上满足：
$\left\{ \begin{array}{l} f\left( x_i \right) =y_i\\ f^{'}(x_i)=y^{'}_i \end{array}\left( i=0,1,2,...,n \right) \right.$
埃尔米特插值仍会产生龙格现象，所以在实际应用中，往往使用分段三次Hermite插值多项式(PCHIP)。

样条插值

样条插值法是一种以可变样条来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的，每一个多项式都是由相邻的两个数据点决定的，这样，任意的两个相邻的多项式以及它们的导数(不包括仇阶导数)在连接点处都是连续的。连接点的光滑与连续是样条插值和前边分段多项式插值的主要区别。

埃尔米特插值

from scipy.interpolate import KroghInterpolator as ki
import numpy as np
import matplotlib.pyplot as plt

np.set_printoptions(suppress=True)  # 不使用科学计数法

x = np.linspace(-np.pi,np.pi, 7, endpoint=True)  # 在[-Π,Π]上生成7个数，包含Π
y = np.sin(x)
new_x = np.array(np.arange(min(x),max(x),0.1))  # 从[-Π,Π]上每隔0.1取一个数，作为待插坐标
interpolant = ki(x, y)  #构造Hermite方法
sin_x = np.array(np.arange(-np.pi,np.pi,0.01))  # 用于绘制三角函数sin

plt.figure()
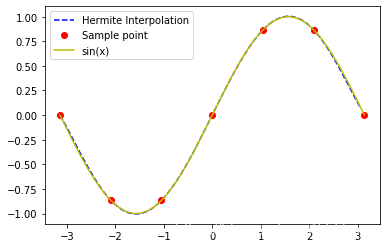
plt.plot(new_x, interpolant(new_x), 'b--',label='Hermite Interpolation')  # 绘制Hermite插值图
plt.plot(x, np.sin(x), 'ro', label='Sample point')  # 原始样本点
plt.plot(sin_x, np.sin(sin_x), 'y-', label='sin(x)')  # 绘制三角函数图sin
plt.legend()  # 显示图例

<matplotlib.legend.Legend at 0x2443a10d448>

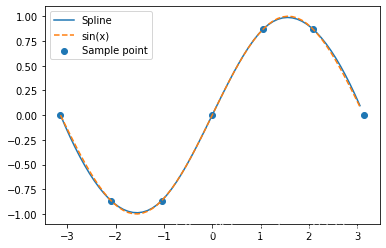
在这里插入图片描述

三次样条插值

import scipy.interpolate
import numpy as np, matplotlib.pyplot as plt
from scipy.interpolate import interp1d

x = np.linspace(-np.pi,np.pi, 7, endpoint=True)
y = np.sin(x)
xx = np.arange(min(x), max(x), 0.1)
_, ax = plt.subplots()
ax.scatter(x, y, label='Sample point')
spline = interp1d(x, y, kind='cubic')  # cubic：三次样条插值，更多方法见http://liao.cpython.org/scipy15/
ax.plot(xx, spline(xx), label='Spline')
ax.plot(xx, np.sin(xx), '--', label='sin(x)')
plt.legend()

<matplotlib.legend.Legend at 0x24439e98ec8>

在这里插入图片描述