数学分析 - 反常积分

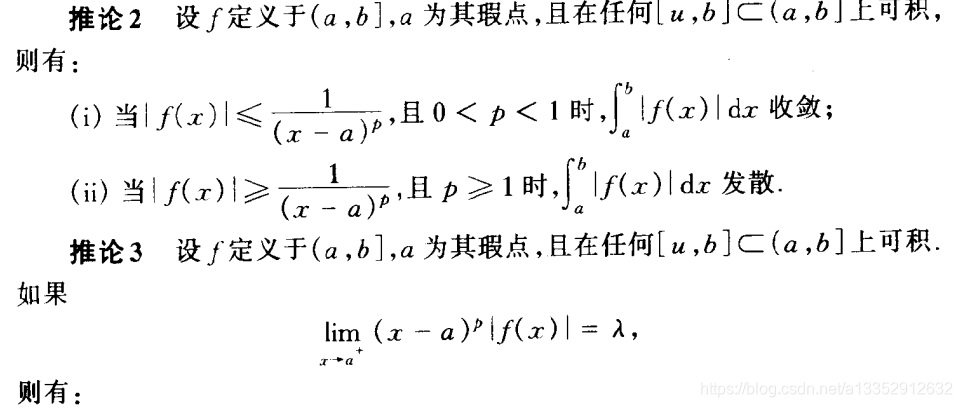
前面的定积分讨论中的两个最基本的限制为：积分区间的有穷性和被积函数的有界性，本章的反常积分将突破这两个限制

---

反常积分的概念

|| 定义一：第一类反常积分的定义
设函数 f 定义在有穷区间[ a,+∞)上，且在定义域内任何的有限区间中都可积。如果存在以下极限，则称极限 j 为函数 f 在[ a,+∞)上的无穷限反常积分（无穷积分）：

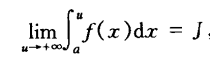
|| 双无穷：在（-∞+∞）上的无穷积分使用两个无穷积分来定义：

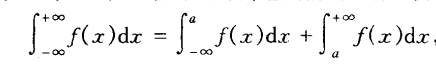
|| 定义二：设函数 f 定义在区间(a, b]上，在点a的任一右邻域内无界，但在定义域内任何有限闭区间内都有界且可积，若存在以下极限，则称此极限为无界函数 f 在 (a, b]上的反常积分（瑕积分）：

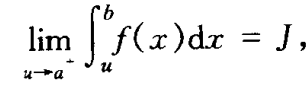
（注意：f 在点a近旁无界，称a为 f 的瑕点）

|| 双瑕点：瑕点为a和 b的瑕积分积分使用瑕积分来定义

---

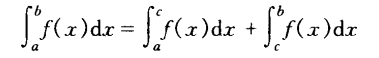
无穷积分的性质和收敛判别

无穷积分的性质

|| 定理1：无穷积分收敛的充要条件（即需要满足极限存在性，使用 柯西准则 即可）
无穷积分∫^+∞_a收敛的充要条件：任给ε>0,存在G≥a，只要u₁,u₂>G,便有：

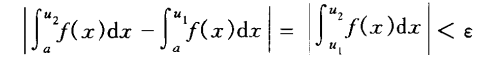
|| 性质1：无穷积分四则运算中的收敛：

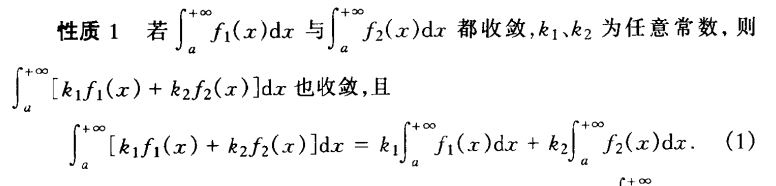
|| 性质2：无穷积分区间相加中的收敛：

|| 性质2的引理： 无穷积分收敛的第二个充要条件：
任给ε>0,存在G≥a，只要u >G,有：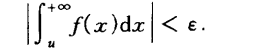

|| 性质3：绝对收敛的无穷积分，自身也必收敛

注意：当∫^+∞_a | f( x) |dx收敛，则称无穷极限为绝对收敛，把自身收敛但是不绝对收敛的无穷积称为条件收敛

|| 定理2：绝对收敛的判断（比较法则）
设函数 f，g 都有无穷积分，且满足 | f(x) | ≤ g(x), x∈[a, +∞），则当∫^+∞_a g( x)dx收敛时， ∫^+∞_a | f( x) |dx 必收敛，∫^+∞_a | f( x) |dx发散时，∫^+∞_a f( x)dx必发散
（即找到其 |f(x)| 上界）

|| 比较法则的推论一：比值常数法

|| 比较法则的推论二和推论三：柯西判别法（使用 1/ x^p作为比较对象）

|| 定理3： 狄利克雷判别法

|| 定理4：阿贝尔判别法

---

瑕积分的性质和收敛判别

|| 定理5：瑕积分收敛的充要条件

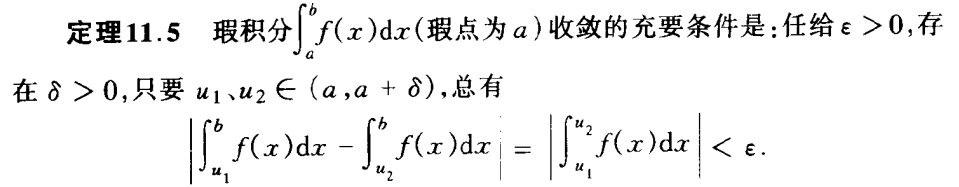
|| 性质1：瑕积分四则运算中的收敛

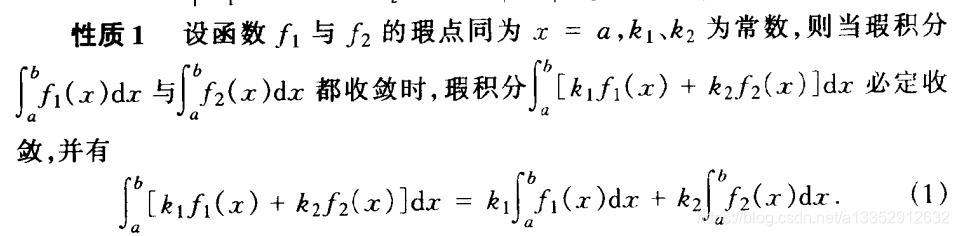
|| 性质2：瑕积分区间相加中的收敛

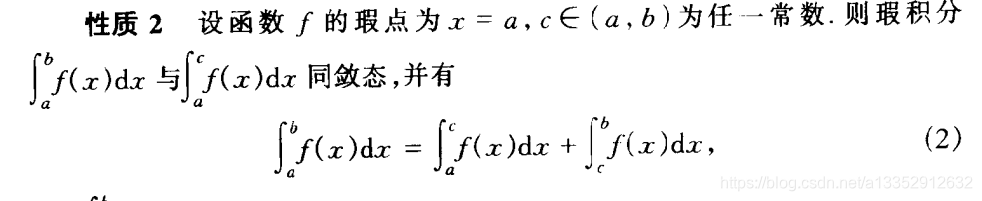
|| 性质三：绝对函数中的收敛

|| 定理6：比较法则

|| 比较法则的推论一：比值常数法

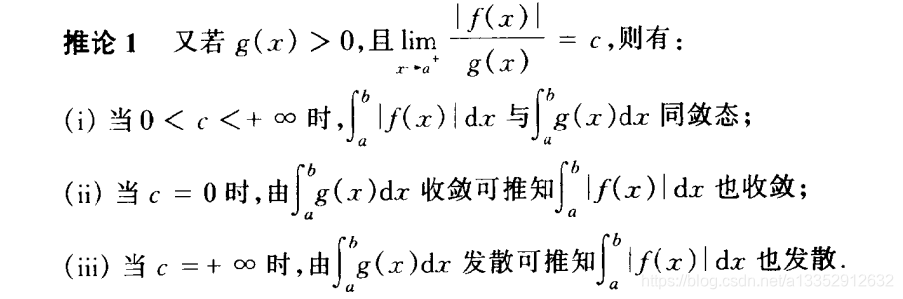
|| 比较法则的推论二和三：柯西比较法 （以 1/(x - a)^p 作为比较对象）