
微分的概念(y的微增量)
|| 引入微分概念的的背景:
具体问题,当原长为x0正方形边长增加△x,则正方形的面积S(x) = x2 的增量为:2△xx0 + (△x)2
又因为第二部分的△x2是关于△x的高阶无穷小量,因此正方形的面积增量可以近似为第一部分2△xx0
,其产生的误差就是一个关于2△x*x0的高阶无穷小量(即边长为△x的小正方形面积)
|| 定义一:在一点上微分的定义
设函数y=f(x) 定义在x0的某邻域U(x0),当给x一个增量△x(△x + x ∈U(x0))时,相应的y的增量为 △y =f(x0 + △x) - f(x0)。若存在常数使得△y = A△x + o(△x),则称函数在x0上可微,并称第一项A△x为 f 在点x0处的微分,记作:d(y)
(注意:微分就是当在△x–>0的情况下的△y的近似值dy。dx,dy可以理解为x,y的微增量(微小的△x,△y)
可微性和可导性的关系
|| 定理1:可微性和可导性的关系定理
函数f在x0上可微的充要条件是函数 f 在x0上可导
|| 注意一:常数A = f '(x0)
根据导数中的有限增量公式 △y = f '(x0) △x + o(△x), 比较△y = A△x + o(△x),可以得到
dy = f '(x0) △x,即A就是 f 在x0上的导数
|| 注意二:函数在一点上的导数,就是在该点上y的微分和x的微分的比值,又称微商【微商?doge】
若将自变量x的增量△x看成自变量的微分dx,那么有dy = f '(x0) △x 可写成 dy = f '(x0) dx,故有f '(x) = dy / dx = lim△x–>0(△y/△x)。
微分的运算
一阶微分的运算法则(类比导数的运算法则)
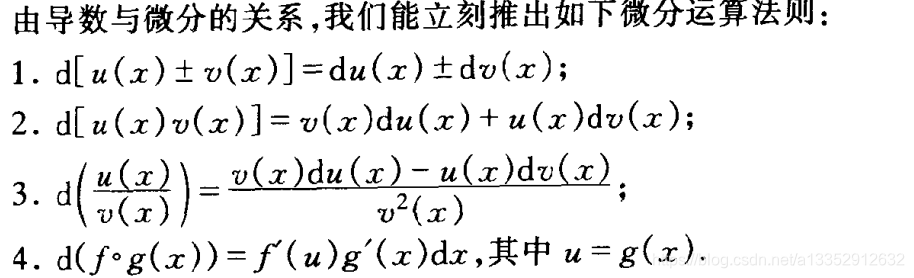
|| 一阶微分形式的不变性 — 针对复合函数的微分式
针对第4个法则,由于du = g ’ (x)dx,故也可以写作dy = f‘(u)du;我们得出结论:dy = f’(x0)dx 不仅在x为自变量时成立,当x为可微函数时同样也成立,这称作一阶微分形式的不变性
高阶微分的运算法则
|| f 的二阶微分公式: d2y = f(2)(x)dx2
(注意:d2x指的是x的二阶微分,dx2指的是dx*dx,d(x2)指的是x2的一阶微分)
|| f 的n阶微分公式: dny = f(n)(x)dxn
|| 复合函数高阶微分的运算
同一阶微分运算法则,但是对于复合函数的高阶微分将不再具有 “一阶微分形式不变性”
微分的一些应用
|| 相对误差计算
|| 函数的近似运算
