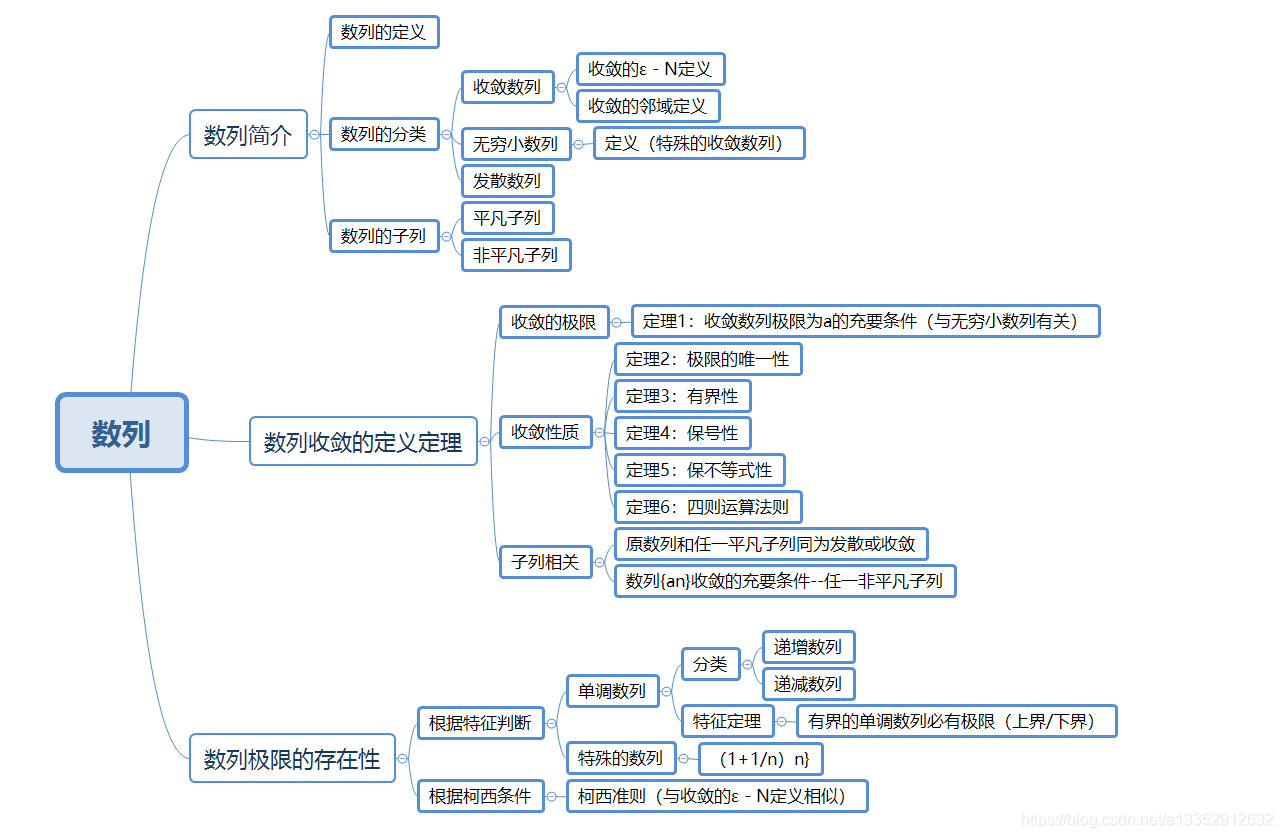
数列的概念
|| 定义一:数列的定义
若函数f 的定义域为全体正整数N+,则称该函数值的集合 f(n),n∈N+为数列,数列可写作 a1,a2,…,an…或简单记作{an},其中an称为数列的通项
|| 定义二: 数列收敛的ε - N定义(“无限接近”转义为“差的绝对值无限小”)
设{an}为数列,a为定数。若给定任意正数ε,总存在某正整数N,使得当n>N时,|an - a| < ε,则称数列收敛于a,定数a称为数列{an}的极限,并记作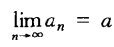
|| 若数列{an}没有极限,则称{an}不收敛,或称{an}为发散数列
|| 关于极限的一些注意事项:
- ε的任意性:ε代表任意小的正数,那么2ε,ε/2,ε2 同样是无穷小的正数,可以替换ε
- 数列收敛的邻域定义:an为数列,a为定数,若存在某个正数ε,若在U(a,ε)之外数列{an}的项至多只有有限个(N个),则称数列{an}收敛于极限a。
|| 定义三:无穷小数列定义
若数列收敛,且极限为0,则该收敛数列称为无穷小数列
|| 定理1:收敛数列极限为a的充要条件
当{an - a}为无穷小数列,收敛数列极限为a
收敛数列的性质
|| 定理2:极限的唯一性
若i数列{an}收敛,则它只有一个极限
|| 定理3:有界性
若{an}收敛,则{an}为有界数列,即存在正数M,使得对一切正整数有 |an| < M
|| 定理4:保号性 (在应用保号性时a` = a / 2)
若limn->∞ an= a,则对任何a’∈(0,a),存在正数N使当n>N时有an>a’
|| 定理5:保不等式性(若n->∞,数列通项的大小关系,即为数列极限的大小关系)
设{an}和{bn}均为收敛数列,若存在正数N,使得当n>N时有an≤bn,则limn->∞ an≤limn->∞ bn
|| 定理6:迫敛性
设{an}和{bn}均为收敛数列,且以a为极限。数列{cn}满足:存在正数N,当n>N时有an≤cn≤bn,则数列{cn}收敛,且limn->∞ cn = a
|| 定理7:四则运法则 加减乘除
若{an}和{bn}均为收敛数列,则{an+ bn},{an- bn},{an* bn}也都是收敛函数且
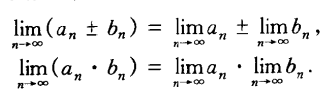
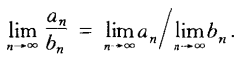
特别的,当bn为常数时也满足上式子(当然除法时bn!= 0)
定义四:子列的定义 (子列其实就是从数列中不连续但按顺序取数组成)
设{an}为数列,{nk}为正整数集N+的无限子集,且n1<n2<…<nk<…,则数列an1,an2,…,ank,…称为{an}的一个子列,简记为{ank}
注意:{an}本身也是一个子列
定义五:平凡子列和非平凡子列
该数列本身和去掉有限项的子列,称为{an}的平凡子列,不是平凡子列的子列称为非平凡子列,例:{a2k},{a2k-1}为非平凡子列
注意:因为平凡子列只删去了有限项,故原数列和任一平凡子列同为发散或收敛(收敛的邻域定义)
定理8:子列与原数列收敛的关系(往往判断数列收敛发散,因为只需要举出一个反例即可证发散)
数列{an}收敛的充要条件是:{an}的任何非平凡子列都收敛,且与原数列共同收敛于一个极限
数列极限存在的条件
对于一些复杂的极限问题,首先要考察数列是否有极限,我们通常需要从数列的本身特征上找到存在性的判断,故以下讨论一些数列
|| 单调数列:递增数列和递减数列(既可用于极限存在性判断,同时是数列收敛的充分条件(有界说明极限为常数))
若{an}各项满足关系an ≤ an+1,则称为递增数列
|| 定理9:单调有界定理
在实数系中,有界的单调数列必有极限(递增数列若有界则必定是上界啦,递减数列若有界则必定是下界啦,其确界就是他们的极限)
|| 特殊的数列{(1+1/n)n} :递增数列有界,且极限用拉丁字母 “e”表示(e≈2.718 281 828 459)
以e为底的对数称为自然对数,通常记 lnx = logex
|| 定理10:柯西收敛准则 (既可用于极限存在性判断,同时是数列收敛的充分必要条件)
数列收敛的充要条件是:数列满足柯西条件(对任给的ε>0,存在正整数N,使得当n,m > N时有 |an - am| < ε)
注意:区别数列收敛的ε-N定义,定数a变成了数列中的am,因此只需要关注数列本身的特征就可以鉴别收敛发散性而不需要借助其他定数a
|| 柯西收敛准则的条件称之为柯西条件:空间意义为当n足够大以后,数列各项的值都挤在了一起(差的绝对值小于任意小的数)
